部分相干双曲余弦高斯光束在湍流中的等效曲率半径

汤明玥，陈晓文，王宇峰

(1． 川北医学院基础医学院;2． 川北医学院影像学院，四川 南充 637000)

激光束在湍流大气中的传输特性是当前国内外热点话题之一，其与卫星遥感、光学雷达、监测、远距离光通讯等紧密相关［1］．湍流环境相当的复杂，因而要求科研工作者们在简化的物理模型下进行数值模拟计算，力求得到与实验更为相近的结果．近年来，国内外诸多科研人员利用多种湍流模型研究了各类激光束在湍流中的传输特性，如:光束扩展、相干性、方向性、光强分布等，并研究证实了部分相干光较完全相干光受湍流的影响更小［2-7］．然而，迄今为止，对于湍流对激光束等效曲率半径的影响方面的研究并不多见，文献［8 -9］研究了部分相干平顶光束、厄米-高斯光束通过湍流传输的等效曲率半径．

另一方面，厄米正弦类高斯光束它代表了一大类光束，如正(余)弦高斯光束和双曲正(余)弦高斯光束［10］．这些光束携带有限能量，可由特殊的切趾光阑或光腔产生．因而，对于部分相干双曲余弦高斯光束的研究是有一定实际意义的．

本文采用更为贴近实验结果的非-Kolmogorov 湍流模型，并选用部分相干双曲余弦高斯(ChG)光束作为激光模型，理论分析了湍流参量和光束参数对等效曲率半径的影响，得到了一些有意义的结果．

1 理论模型

设部分相干双曲余弦高斯(ChG)光束在源场(z=0)处的交叉谱密度函数表示为［10］

其中，w0和σ0分别为z=0 处光束的束腰和相干长度，Ω0为与双曲余弦有关的光束参数［10］．

根据广义惠更斯-菲涅尔原理，光束通过自由空间传输的平均光强表示为［11］:

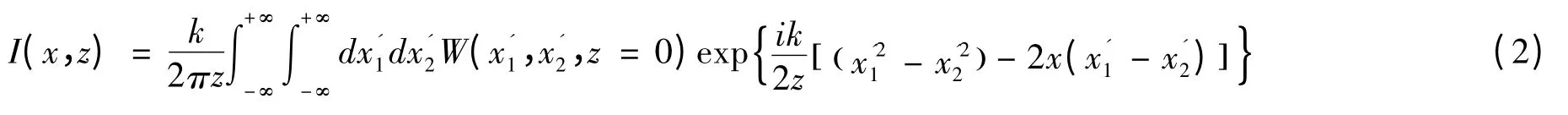
其中，k 是波数(k=2π/λ)，λ 为波长．

光束沿x 方向的空间二阶矩的定义为［11］:

将(2)式代入(3)式，并引入新的变量．经过复杂的积分运算可得部分相干ChG 光束在自由空间中传输时沿x 方向的空间二阶矩为:

上式中

其中，β=σ0/w0为光束相干参数，δ=Ω0w0为光束离心参数．

若光束在湍流中传输，则二阶矩〈x2〉与〈xθx〉可写为［12］

其中T 为表征湍流的参量，表达式为［13］

由于利用非-Kolmogorov 湍流模型的理论研究结果与实验数据更为接近，本文采用非-Kolmogorov 统计，Φn(κ，α)可表示为［13］

上式中，κm=c(α)/l0，κ0=2π/L0，l0和L0分别为湍流的内尺度及外尺度，为广义折射率结构函数(单位为m3-α)，α 为湍流广义指数．若即简化为常规Kolmogorov 功率谱．

等效曲率半径可用二阶矩定义为［14］

因而，部分相干ChG 光束在湍流中传输的等效曲率半径解析表达式为

上式表明，部分相干ChG 光束通过湍流传输的等效曲率半径Rx(z)与光束参数(w0、β、δ、λ)及湍流参数相关．

2 数值计算结果与分析

对部分相干ChG 光束通过湍流传输的等效曲率半径Rx(z)及相对等效曲率半径Rx/Rxfree随各参量的变化情况进行了数值分析，依据实际激光束在湍流中传输时各参数取值范围，令计算参数λ=1．06 ×10-6m、w0=0．05m、β=0．1、δ=2、z=10km、L0=20m、l0=0．01m．

图1 为等效曲率半径Rx(z)随折射率结构常数的变化，其中令α=11/3．图1 说明等效曲率半径Rx(z)随湍流的增强而逐渐减少，即湍流使得光束的等效曲率半径减小．图2 为Rx(z)随湍流广义指数α 的变化情况，Rx(z)随α 的增大而先减小后增大，且在α =3．11 时存在Rx(z)的极小值．这是因为Rx(z)与湍流的大小相关，而湍流对广义指数α 的非线性变化必然直接影响其Rx(z)随α 的变化趋势．

已有文献［8-9］对等效曲率半径随光束参数的变化展开了研究，但离心参数对等效曲率半径的影响尚未涉及．图3 给出了自由空间及湍流中部分相干ChG 光束等效曲率半径Rx(z)随离心参数δ 的变化情况(其中，，实线表示自由空间，虚线表示湍流空间．可以看出不论在自由空间或湍流中，Rx(z)都随δ 的增加而增加，但湍流使得其变化更加缓慢．为更直观呈现湍流对等效曲率半径的影响，引入相对等效曲率半径Rx(z)/Rxfree随δ 作图，见图4．图4 表明Rx(z)/Rxfree随δ 的增加而减小(湍流使得等效曲率半径变小)，这说明δ 越大，湍流对Rx(z)的影响越大，但不同δ 值的光束Rx(z)受湍流影响的差别不大．

图1 Rx(z)随 的变化Fig．1 Rx(z) versus

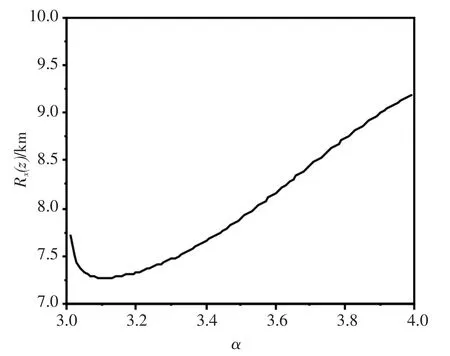
图2 Rx(z)随α 的变化Fig．1 Rx(z) versus α

图3 Rx(z)随δ 的变化Fig．1 Rx(z) versus δ

图4 Rx(z)/Rxfree 随δ 的变化Fig．1 Rx(z)/Rxfree versus δ

3 结 论

基于非-Kolmogorov 湍流模型，给出了部分相干ChG 光束在非-Kolmogorov 湍流中的等效曲率半径解析表达式，并研究了湍流参量与光束参数对等效曲率半径的影响．研究指出:部分相干ChG 光束在湍流中的等效曲率半径Rx(z)随湍流的增强而逐渐减小;随湍流广义指数α 的增大而先减小后增大，且在α=3．11 时存在Rx(z)的极小值．

部分相干ChG 光束传输于自由空间或湍流中，等效曲率半径Rx(z)都随离心参数δ 的增加而增加，但湍流使得其变化更加缓慢．此外，引入相对等效曲率半径Rx/Rxfree研究发现，δ 越大，湍流对Rx(z)的影响越大，但不同δ 值的Rx(z)受湍流影响的差别不大．

［1］ ANDREWS L C，PHILLIPS R L． Laser Beam Propagation through Random Media［M］． Bellingham:SPIE Press，1998．

［2］ YOUNG C Y，GILCHREST Y V，MACON B R． Turbulence Induced Beam Spreading of Higher Order Mode Optical Waves［J］． Opt． Eng．，2002，41(5):1097 -1103．

［3］ SHIRAI T ，DOGARIU A，WOLF E． Mode Analysis of Spreading Coherent Beams Propagating Through Atmospheric Turbulence［J］． Opt． Lett，2003，20(6):1094 -1101．

［4］ CHEN XIAOWEN，JI XIAOLING． Directionality of Partially Coherent Annular Flat-topped Beams Propagating Through Atmospheric Turbulence［J］． Optics Communications，2008，281(18):4765 –4770．

［5］ 陈晓文，李宾中，汤明玥． 部分相干厄米高斯光束的湍流距离［J］． 西华师范大学学报(自然科学版)，2014，35(1):82-86

［6］ 陈晓文，汤明玥，季小玲． 大气湍流对部分相干-厄米高斯光束空间相干性的影响［J］． 物理学报，2008，57(4):2607-2613．

［7］ 汤明玥，李宾中，王宇峰，等． 非Kolmogorov 湍流对高斯-谢尔光束的瑞利区间和湍流距离的影响［J］． 中国激光，2014，41(10):1013002．

［8］ 季小玲． 部分相干平顶光束通过湍流大气传输的等效曲率半径［J］． 物理学报，2010，59(6):3953 -3958．

［9］ JI GUANGMING，JI XIAOLING． Effective Radius of Curvature of Hermite-Gaussian Array Beams［J］． Optics and Laser Technology，2010，42(6):1054 -1058．

［10］ CASPERSON L W，HALL D G，TOVAR A A． Hermite-Sinusoidal-Gaussian Beams in Complex Optical Systems［J］． JOSA A，1998，15(4):954 -961．

［11］ CHEN XIAOWEN，TANG MINGYUE，HE CHAO，et al． Spreading of Apertured Partially Coherent Beams in Turbulent Media［J］．Optik，2014，125:6032 -6036．

［12］ 黄永平，赵光普，肖 希，等． 部分空间相干光束在非Kolmogorov 湍流大气中的有效曲率半径［J］． 物理学报，2012，61(14):144202．

［13］ 邓金平，季小玲，陆 璐． 多色部分相干偏心光束在non-Kolmogorov 湍流中的传输［J］． 物理学报，2013，62(14):144211．

［14］ 邵晓利． 激光束通过大气湍流传输的等效曲率半径特性研究［D］． 成都，四川师范大学，2012．