一种时滞系统输出反馈自适应稳定的改进方法

许建强， 李俊玲

（上海应用技术学院理学院，上海 201418）

一种时滞系统输出反馈自适应稳定的改进方法

许建强， 李俊玲

（上海应用技术学院理学院，上海 201418）

针对一类含变时滞状态扰动不确定系统的输出反馈自适应稳定问题，已有的算法仅能保证闭环系统状态最终一致有界.提出了一种新的控制算法，通过在控制器中引入一正的一致连续有界函数并设计了一种新的自适应率对扰动参数进行在线估计，可以保证闭环系统的状态一致渐近趋于零.仿真结果验证了该算法的有效性.

时滞系统；输出反馈；自适应稳定；一致渐近稳定

时滞的存在往往是系统不稳定或系统性能变差的根源.在许多实际系统中，状态往往不易测量或不能直接测量得到，因而在物理上实现状态反馈控制器并不容易.因此，近年来在时滞系统中引入输出反馈控制越来越受到了人们的关注［1-3］.文献［4］中在要求不确定性的上界是已知的条件下，首先研究了含时滞状态扰动不确定系统的输出反馈自适应稳定问题.文献［5］中则对不确定性的上界做了进一步的推广，假定上界是某些已知函数的线性组合但系数未知，通过设计自适应状态观测器保证了状态估计一致渐近趋于系统的真实状态.在上述研究中，时滞都是常数.同常时滞相比，变时滞的研究结果则要少得多.文献［6］在文献［4-5］的研究基础上，进一步假定不确定性上界是未知的和时滞是变化的情形，通过对不确定性上界进行在线估计，设计自适应输出反馈控制器，使得闭环系统状态最终一致有界.

本文在研究了文献［6］中的含时滞扰动不确定非线性系统的输出反馈自适应稳定问题的基础上，在自适应控制器的设计中引入了一正的一致连续有界函数，并采用了不同的自适应律对系统的未知参数进行在线估计，进而保证了闭环系统状态一致渐近趋于零.

1 系统的描述

考虑一类包含非线性变时滞扰动的不确定系统

式中：时间t∈R；状态x（t）∈Rn；控制输入是系统输出；A，B，C是具有适当维数的常数矩阵代表含时滞扰动的未知非线性向量函数.初始条件是一个定义在上的连续函数，h（t）是时变时滞且满足

系统（1）的标称系统为

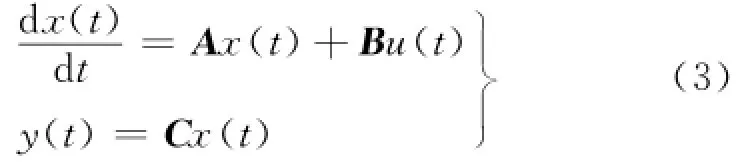
2 主要结果

假设1 ｛A，B｝是完全可控的.

假设2［4］未知向量函数G是连续的，且满足下述不等式：

式中：‖·‖表示欧几里德范数；βj，j=1，2，3是未知常数.不访设.

注1 由Kalman-Yakubovich引理［7］可知：T（s）是严格正实的充要条件是存在正定阵P∈和反馈矩阵K∈Rm×n满足

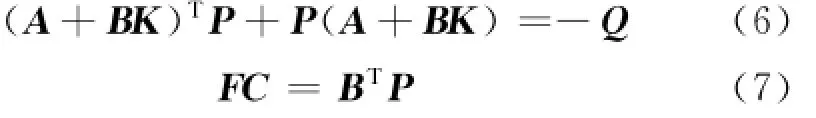
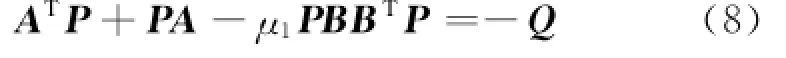
有对称正定解P∈Rn×n.显然，当时，式（8）和（6）是等价的.

引理1［8］已知则对任意的0，有

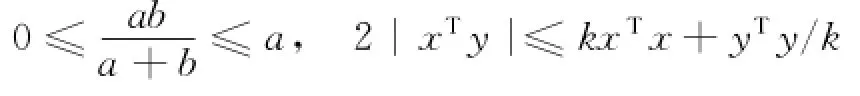
引理2［8］Barbalat引理若函数f（t）在［0，上一致连续，并且广义积分存在，则有

定理1 对于满足假设1～3的系统（1），若采用由如下形式的自适应输出反馈控制器和自适应律

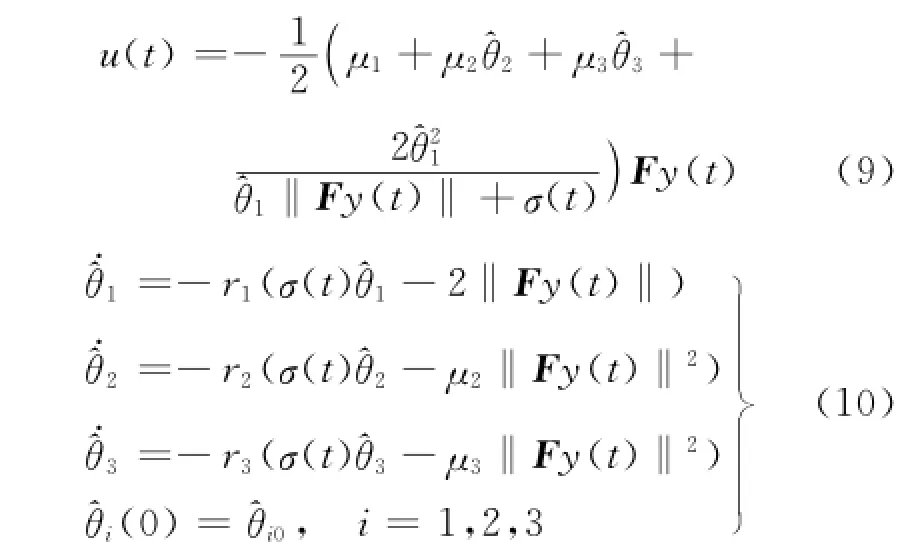
式中，F称为输出控制增益矩阵，它使得式（5）中的传递函数T（s）是严格正实的.σ（t）∈R+是一正的一致连续有界函数满足

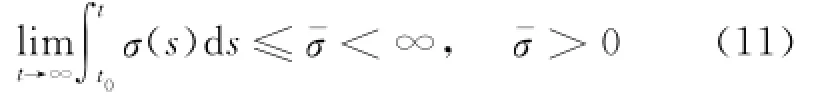
μi＞0，i=1，2，3，且满足

证明 构造如下形式的Lyapunov-Krasovskii函数

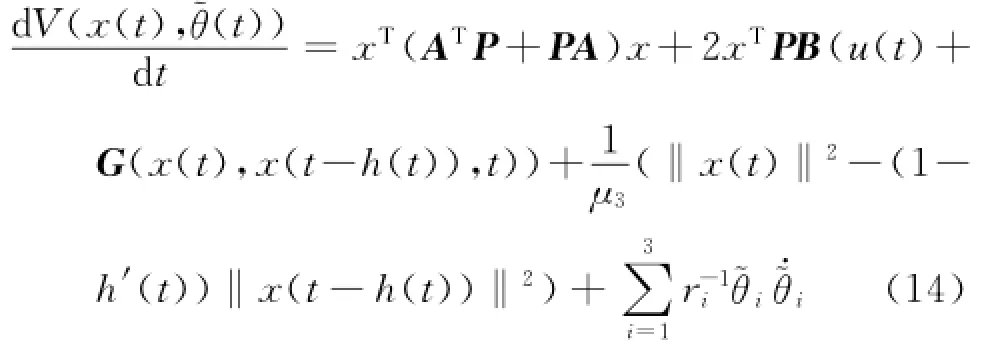
将式（9）代入式（14）并注意到

所以

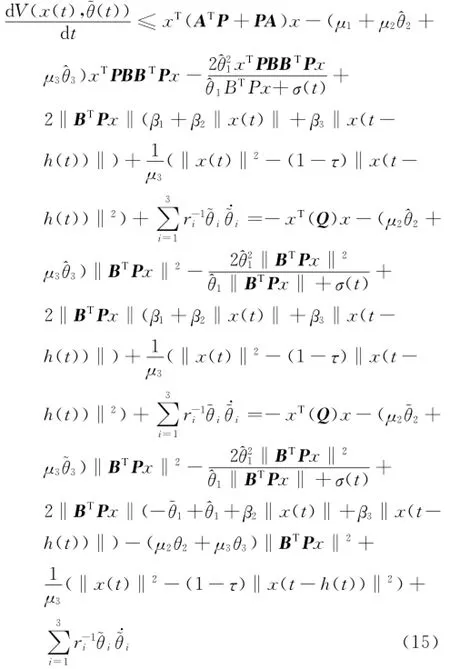
由引理1可得

将式（16～18）代入式（15）可得

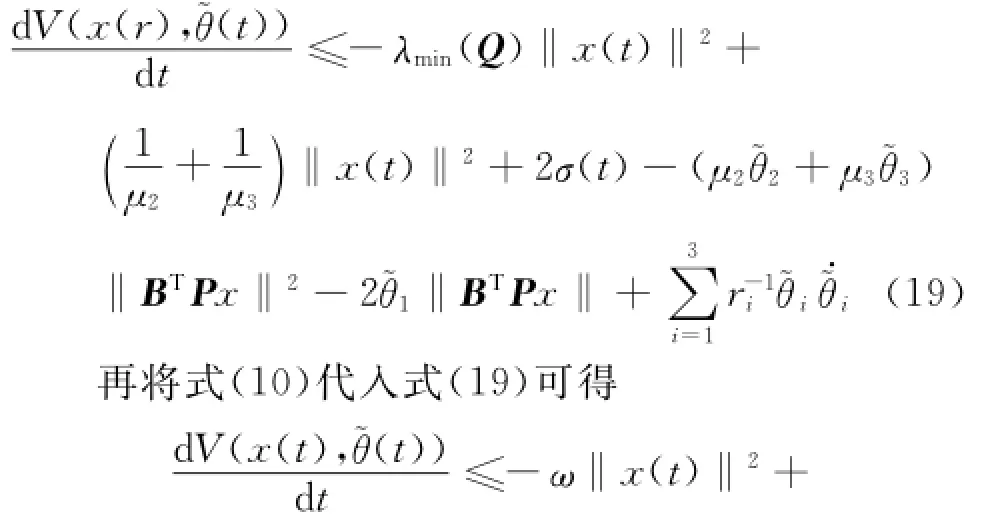
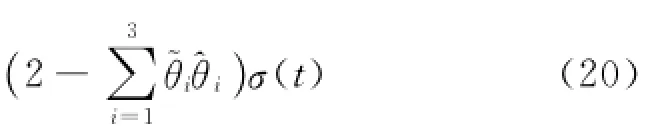
式中，

由不等式a2+b2≥2ab可得

式中，

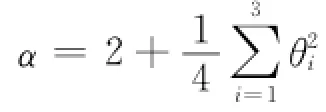
由式（22）可知：由式（1）、（9）和（10）构成的闭环系统是一致最终有界的.

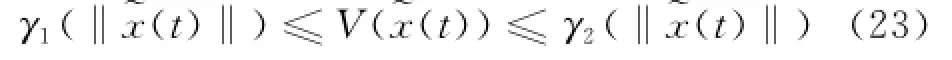
式中，

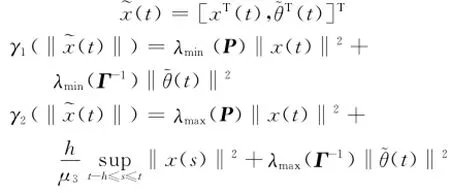
所以，由式（22）、（23）可得

式中，

对式（24）两边取极限并结合式（11）可得

另一方面，由式（23）可得

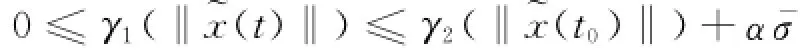
即~x（t）是一致有界.易知，~x（t）连续，所以~x（t）一致连续，从而γ3（‖x（t）‖）一致连续.由引理2知

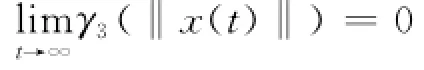
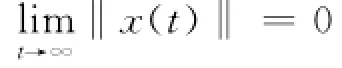
即系统的状态将一致渐近趋于零.

3 仿真实例

考虑如下含变时滞扰动的非线性不确定系统［6］

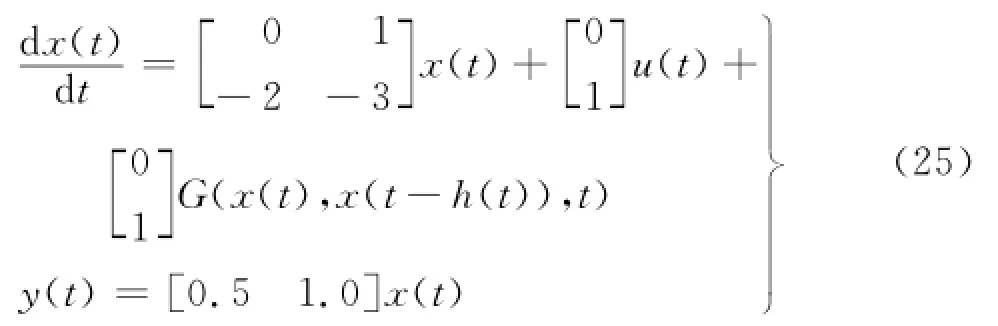
式中，

易证，当F=2时，标称系统的传递函数矩阵

是严格正实的.由式（6）可得

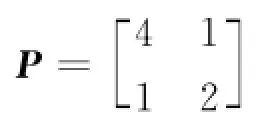
令μ1=2，则由矩阵黎卡提方程式（8）可求得

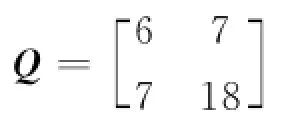
在本例中，取

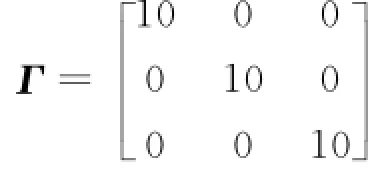
μ2=0.65，μ3=1.显然，

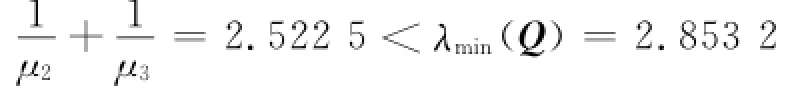
时滞h（t）=1+0.5sin t，如图1所示.

图1 时滞函数Fig.1 Time-delay function

取σ（t）=25e-0.5t，采用由式（9）给出的自适应输出反馈控制器和式（12）给出的自适应率的仿真结果如图2所示.

图2 系统输出响应Fig.2 Response of output system

4 结 语

针对一类含时滞扰动不确定非线性系统的输出反馈自适应稳定问题.假定不确定性满足所谓的匹配条件且标称系统的传递函数矩阵是严格反馈正实的.提出了一种新的自适应控制方法，在自适应控制器的设计中引入一正的一致连续有界函数，并证明了此控制器使得闭环系统一致渐近趋于零.仿真结果也表明了该算法的有效性.

［1］ Hua C，Guan X.Output feedback stabilization for time-delay nonlinear interconnected systems using neural networks［J］.IEEE Trans Neural Networks，2008，19（4）：673-688.

［2］ Yoo S J.Adaptive neural output-feedback control for a class of non-linear systems with unknown time-varying delays［J］.IET Control Theory Appl，2012，6：130-140.

［3］ Yan X G，Sarah K S，Edwards C.Decentralized stabilization for nonlinear time delay interconnected systems using static output feedback［J］.Automatica，2013，49（2）：633-641.

［4］ Wu H S.Robust output feedback controllers for dynamical systems including delayed perturbations［J］. International Journal of Systems Science，1999，30（2）：211-218.

［5］ Wu H S.Adaptive robust state observers for a class of uncertain nonlinear dynamical systems with delayed state perturbations［J］.IEEE Trans Automatic Control，2009，54（6）：1407-1412.

［6］ 许建强，陈树中.含时滞扰动非线性系统的输出反馈自适应控制［J］.华东师范大学学报：自然科学版，2006（3）：60-65.

［7］ Khalil H K.Nonlinear systems［M］.New York：Mac-Millan，1992.

［8］ 梅生伟，申铁龙，刘康志.现代鲁棒控制理论与应用［M］.北京：清华大学出版社，2003.

（编辑 俞红卫）

An lmprovement of Output Feedback Adaptive Stabilization for Time Delay System

XU Jian-qiang， LI Jun-ling
（School of Sciences，Shanghai Institute of Technology，Shanghai 201418，China）

As for the problem of output feedback adaptive stabilization for a class of uncertain dynamic system including time-varying delayed disturbance，the old algorithm only guaranteed the uniform ultimate boundedness of the closed-loop system.A new control algorithm was proposed.A positive uniformly continuous bounded function was introduced in the controller and a new adaptive law was designed to estimate the parameter of the disturbance on line，which could guarantee the state trajectory of the closedloop system was uniformly and asymptotically to zero.The effectiveness of the algorithm was verified by the simulation results as well.

time delay system；output feedback；adaptive stabilization；uniformly asymptoticallystabilization

O 231.2

A

1671-7333（2015）01-0099-04

10.3969／j.issn.1671-7333.2015.01.018

2014-07-28

许建强（1973-），男，副教授，博士，主要研究方向为控制理论与应用.E-mail：jqxu＠sit.edu.cn