基于数据挖掘技术的概率统计教学研究

马红娟，赵秀兰，孙亚萍，郑喜英

（1.黄河科技学院 信息工程学院，郑州 450063；2.郑州城轨交通中等专业学校，郑州 450000）

引言

高速发展的信息技术产生了大量的数据，人们收集这些数据，在给我们生活提供方便的同时，带来一些问题。由于收集的数据不断增多，在对数据进行挖掘的过程中对所隐藏的数据知道的方法比较少，使得数据囤积量增大，由于数据库里的量，在以几何形式不断增长，要在数据库中对信息去伪存真、去粗存精，靠传统方法是不够的，要想高效地组织、管理这些数据进行分析和应用，数据挖掘是对计算机系统提供更高层次数据分析的最有效的方法。数据挖掘是知识发现的核心部分，从数据集合中自动抽取隐藏在数据中的游泳信息的非平凡过程，表现形式为：概念、规则、模式及规律等。数据挖掘融合了统计学、模式识别、数据库、神经网络、机器学习、空间数据、数据可视化、人工智能、信息检索、高性能计算等多个领域的理论和技术，是一门交叉学科。

一、数据挖掘在概率统计教学实践中的初步应用

在民办高校概率论与数理统计教学实践中，学生是主体，存在着教师对学生课程管理、成绩管理、教学仪器管理、学生管理等各种数据系统。在这些数据库中存储了大量的数据，隐藏在这些数据背后的信息一直未得到开发应用。学生是民办高校的核心，学生的概率统计学习成绩作为一种总结性评价，能反映出他们的概率统计知识技能的获得情况和相应概率统计知识掌握情况，概率统计学习成绩是一个加权的综合数值，不仅包括概率统计书面的考试成绩，而且还包括一些人文的考核项目，比如出勤率、课题表现、各种活动等。学生概率统计成绩不仅对学生的概率统计学习效果和教师的概率统计教学效果具有检验作用，而且还能反馈教学活动，反作用于学生的学和教师的教。一般对学生成绩的评定分为两种：一种是定性评价，一种是定量评价。定性评价一般分为优、良、中、差等四个级别，定量评价是概率统计课程考了多少分。仅仅从单独一门概率统计课程进行分析，很少关注到学生取得这些概率统计成绩背后的影响因素和原因。数据库是从定性分析的角度分析学生，缺点是结果不精确；数据仓库是从定量的角度分析，能精确得到各个方面的数据。使用数据挖掘技术和数据仓库对学生概率统计成绩进行深层的分析，挖掘出隐藏在数据背后的模式或规律，根据数据挖掘结果提出一些指导性建议，更好地指导概率统计教师的教学，提高概率统计教学效率，有效地提高学生概率统计成绩。

二、决策树中的ID3算法

数据挖掘技术主要有遗传算法、决策树法、集合论法、神经网络法等。决策树法分为CLS算法、ID3算法、IBLE算法等。ID3算法是由Quinlan首先提出的，该算法以信息论为基础，以信息增益度和信息熵为衡量标准，从而实现对数据的归纳分类。

已知有C个结果的训练集S：

Entropy（S）=∑-p（I）log2p（I） （1）

这里：p（I）是属于类I的S的比例。∑是对C求和。log2以2为底的自然对数。

如果所有S属于相同的类，熵为0（数据分类完毕）。熵的范围是0（分类完毕）到1（完全随机）。

注意：S不但是属性而且也是整个样本集（这一点刚开始可能有点混淆）。

Entropy（S，A）=∑（|Sv|/|S|）*Entropy（Sv） （2）

这里：∑是属性A的所有可能的值v；Sv=属性A有v值的S的子集；|Sv|=Sv中元素个数；|S|=S中元素个数。

Gain（S，A）是属性A在集S上的信息增益，定义为：

Gain（S，A）=Entropy（S）-Entropy（S，A） （3）

Gain（S，A）是指已知属性A的值后导致熵的减少。Gain（S，A）越大，说明选择检测属性A对分类提供的信息越多。

三、实例分析

通过对概率统计课程学生成绩评定的典型案例，说明数据挖掘的步骤和决策树方法在概率统计教学实践中的应用。

（一）分析对象

概率论与数理统计课程每学年考核一次，考核分为三个部分：一是概率统计课内教学；二是概率统计课后作业；三是每学年期末概率统计考核。整个概率统计课程主要依据在规定时间内完成的概率统计课后作业的质量和期末概率统计考核成绩来决定，概率统计实验课作为较次要的考核内容。上述概率统计教学内容之间的关系，可以建立一个数据模型：学生状况数据库，包含学号、性别、作业、实验课、期末考核、平均成绩、名次等项目。

（二）已知条件

选择两个不同的班，每班30人，两班60人，对学生状况数据库进行如下的量化、转换、清理、集成等处理工作，得到相应的数据仓库（如表1所示），方便下一步数据挖掘的工作。

表1 学生状况数据库

学号字段定义为1—60；性别字段定义为：男或女；作业加分定义为：0表示作业错误，0.5表示作业正确一部分，1表示作业全部正确；实验加分定义为：0表示基本不上概率统计实验课，0.5表示适当上实验课，1表示按期上实验课；期末加分定义为：0表示基本不参加概率统计期末考核，0.5表示参加期末考核取得了较好的成绩；平均分定义为：学习成绩总体情况，字段值为0-100（%）；名次定义为1-60，且记录按名次从高到低排列。

（三）数据挖掘

应用ID3算法建立相应的决策树，确定正例个数p和反例个数n。将名次排在前20名成绩好的学生定义为正例，后40名成绩不好的学生定义为反例，即p=20，n=40。

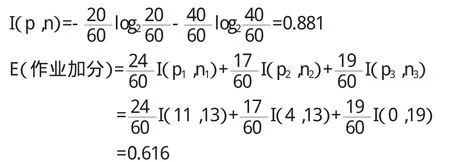
∴gain（作业加分）=I（p，n）-E（作加）=0.881-0.616=0.265同理，gain（实验加分）=I（p，n）-E（课加）=0.881-0.801=0.08 gain（期末加分）=I（p，n）-E（测加）=0.881-0.879=0.002通过计算可知，作业加分具有最大的信息增益，故将作业加分选为根节点并向下扩展，最终生成决策树（如图1所示）。

（四）结论分析

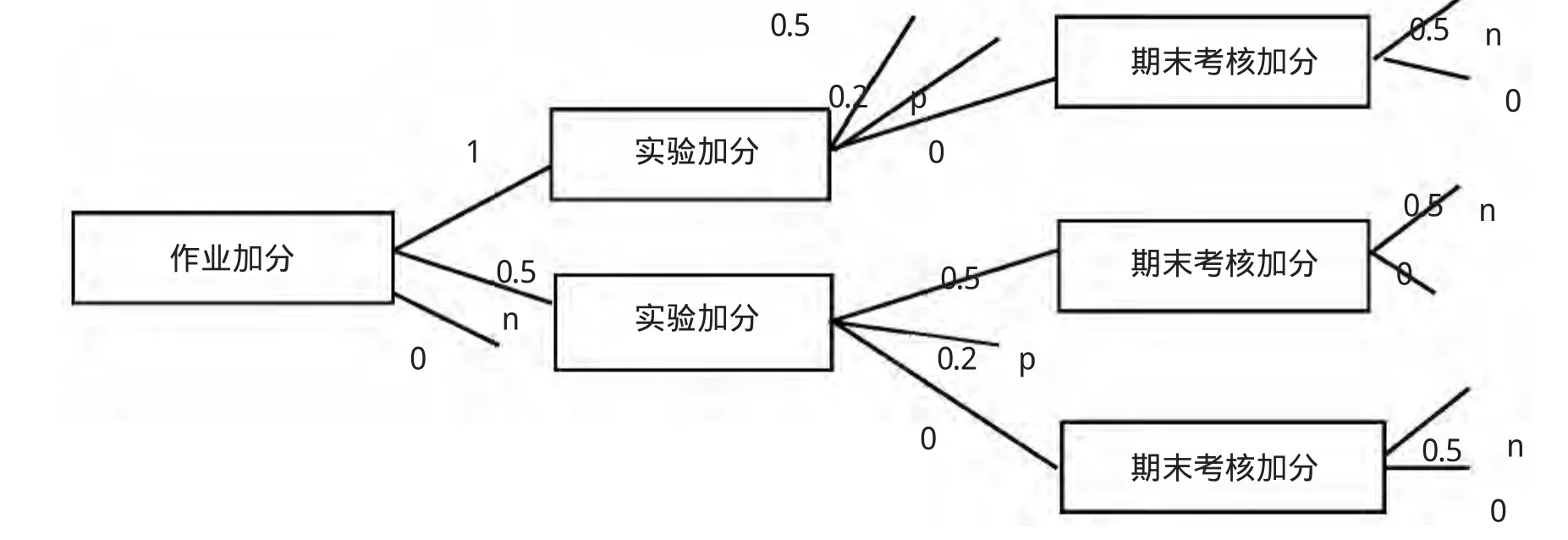
图1 成绩分析决策树

结合上页图1决策树，经过分析可以得到以下结论：

（1）学生上完概率统计课后，如按期并且独立保质保量按时完成概率统计作业，成绩均较好。

（2）学生概率统计作业完成的较好的，也就是在概率统计课堂上思考能力较强，善于思考和分析，可以看出他们在概率统计的基础上较为重视归纳和总结，均没有过重的课内压力，其中概率统计课内安排适度的学生学习成绩也好。

（3）对于刚通过概率统计测评的学生，情况较为复杂，具体情况具体分析，一方面学生的概率统计作业、课内实验、期末考核安排合理时学习成绩也好，另一方面，如果学生经常不参加概率统计课程讲授或不参加概率统计期末考核时，也会影响到学习成绩，造成学习成绩不好。

根据P221表1和图1，对学生情况数据库所建决策树进行分析，可以初步判别：概率统计作业、概率统计实验课、概率统计期末考核是相辅相成的，相互影响和制约，一般来说，学习成绩较好的学生，也是概率统计实验课和期末考试积极参加者。

这样，教概率统计的老师可以针对不同的学生，对学生进行事先概率统计辅导，使教学内容在时间上得到延伸，学生能够提前预习和掌握概率统计教学内容，可以减轻学生在上概率统计课的压力，既紧张又轻松完成预期概率统计课程。同时，也要看到，如果仅重视上概率统计课和参加期末考试而不重视概率统计作业同样也会影响到自身的学习成绩，对于概率统计这门课程，学习成绩好的学生，他们的上进心、责任心也相对较强，能够很好地处理上述三者之间的关系；反之，对自己约束能力较差，经常不上概率统计课，或不认真完成概率统计作业的学生，学习成绩自然就较差。

四、数据挖掘技术的进一步改进与探索

随着越来越多的业务需求被不断开拓，除上述在高等民办院校概率统计课程教学实践中的应用外，数据挖掘技术已成功地应用于医学、商业、科学研究等领域，有很多成功的应用案例。多种理论与方法的合理整合式大多数研究者采用的有效技术，下面是数据挖掘技术发展趋势：（1）数据挖掘语言的标准化描述：标准的数据挖掘语言有助于数据挖掘的系统化开发。改进多个数据挖掘系统和功能间的互操作，促进在企业和社会中的应用。

（2）寻求数据挖掘过程中的可视化方法：可视化要求已经成为数据挖掘系统中不可少的技术。通过人机界面可以在发现知识的过程中进行很好的人机交互。数据的可视化推动人们主动进行知识发现的作用。

（3）与特定数据存储类型的适应问题：根据不同的数据存储类型的特点，进行针对性的研究是必须面对的问题。

（4）网络与分布式环境下的KDD问题：随着网络不断发展，网络资源日渐丰富，需要独立的技术人员各自独立地处理分离数据库的工作。考虑适应分布式与网络环境的关系，技术及系统将是数据挖掘中一个最为重要和繁荣的子领域。

（5）应用的探索：随着数据挖掘的日益普通，应用范围日益扩大，如电信业、零售业、生物医学等领域。由于数据挖掘在处理特定应用问题时存在局限性，目前的研究趋势是开发针对于特定应用的数据挖掘系统。

（6）数据挖掘与数据库系统以及Web数据库系统的集成：数据库系统和Web数据库已经成为信息处理系统的主流。数据挖掘系统的理想体系结构是与数据库和数据仓库系统的紧密结合。

结束语

数据挖掘技术作为一种新兴的数据分析技术，经过了十几年的充实和发展，到目前为止已经成功地运用在各个不同的领域。伴随着科学技术的不断发展和信息量的海量增加，比如依靠传统的方法要在庞大的数据库中找到具有科学决策的信息是非常困难的，数据挖掘技术就是从大量的数据中发现有用的知识和线索，借助于数据挖掘本身的技术去挖掘蕴藏在数据库中的客观规律，从而为科学合理的决策提供有力的支持。将数据挖掘技术引入到概率统计教学中，有助于在日常概率统计教学管理中不断获得有规律的信息，为民办高校管理层提供决策依据，从而不断提高概率统计教学质量。本文通过对概率统计课程学生成绩的评定的案例分析，阐述了数据挖掘技术在分析影响学生学习成绩因素中的重要意义，目的是推广数据挖掘技术在民办高校教学实践中的应用，使数据挖掘技术在民办高校得到进一步发展。

[1]盛骤，谢式千，潘承毅.概率论与数理统计：4版[M].北京：高等教育出版社，2010.

[2]谭旭，王丽珍，卓明.利用决策树挖掘分类规则的算法研究[J].云南大学学报，2000，(6)：415-419.

[3]路延.数据挖掘技术在高等学校教学中的应用研究[J].科技教育，2013，(13)：201.

[4]朱迪茨.实用数据挖掘[M].北京：电子工业出版社，2004：77-79.