模块化多电平换流器动态相量建模

夏黄蓉 韩民晓 姚蜀军 万 磊

（1.华北电力大学电气与电子工程学院 北京 102206 2.中国电力科学研究院 北京 100192）

0 引言

模块化多电平换流器（Modular Multilevel Converter，MMC）因具有易扩展、可靠性高、谐波含量少、损耗低等优点[1]，已成为大容量柔性直流输电（Voltage Source Converter based High Voltage Direct Current Transmission，VSC-HVDC）领域的研究热点。截止到2015年7月，我国已在上海南汇、广东南澳和浙江舟山建成了基于MMC的柔性直流输电示范工程，并先后投入运行。

国内外针对MMC的建模进行了大量研究。文献[2]在环流抑制良好的情况下提取上下桥臂电感，在交流侧并联成一个，从而得到了简化等效的电磁暂态模型，该模型适用于MMC的控制策略分析，却无法解决电磁暂态仿真速度慢的问题。文献[3]提出超大规模MMC电磁暂态仿真提速模型，将仿真计算中的超大规模节点导纳矩阵降为多个低阶矩阵同时求解，提高了原有电磁暂态模型的仿真速度，但在电平数较高的情况下仿真时间仍然较长。文献[4]在“准稳态”假定条件下提出了MMC机电暂态模型，该模型能够反映系统外特性，适用于潮流计算等快速仿真，但是仿真精度不高，不能分析桥臂电容电压和环流等MMC内部特性。文献[5]将开关函数和瞬时功率结合，建立了考虑2次环流的MMC时域解析数学模型，该模型计算复杂，不适用于分析交直流侧更高次谐波，且不能直观反映MMC内部变量的关系。文献[6]在模块均压及忽略系统高频分量的前提下，通过选取上、下桥臂电容电压之和及之差，以输出电流与环流为状态变量，建立了系统的状态方程，进而建立了MMC等效模型，但是该模型无法直接求解直流侧2次环流。

本文引入动态相量法[7-12]，建模分析MMC换流器。在MMC开关函数模型和基于状态方程的等效模型的基础上推导动态相量模型，并在Maltab中编写以各阶动态相量为状态变量的状态方程进行计算，与应用Matlab/Simulink仿真软件得到的电磁暂态模型进行对比。结果表明，所提动态相量模型在稳态和暂态情况下均可靠。本文以2次环流计算为例，说明MMC动态相量模型可根据仿真需求选取谐波阶次，快速地计算出交直流侧电压、电流的各次谐波分量。

1 动态相量法

动态相量法的本质是时变的傅里叶级数，时域函数x(τ)的周期是T，在τ∈(t−T,t]区间内将其用傅里叶级数表示为

式中，ωs=2π/T；Xk(t)为k阶动态相量，其在时刻t的值可由一个周期内的平均运算得到

与常规运算相比，动态相量运算的特殊性体现在微分特性、卷积特性和共轭特性上。

（1）微分特性

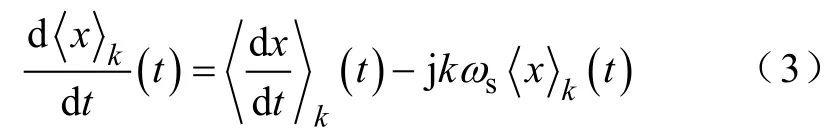
（2）卷积特性

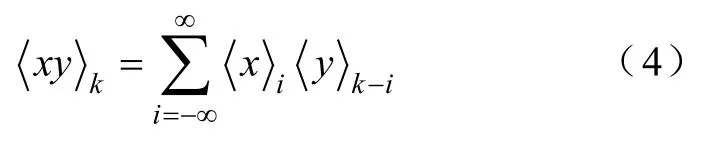
（3）共轭特性

对时域信号进行傅里叶分解得到各阶动态相量后，为了简化分析，一般保留相量中幅值较大的阶次，忽略幅值较小的阶次。这样适当简化了的电磁暂态模型的精度和仿真速度介于电磁暂态模型和机电暂态模型之间，在包含大量电力电子器件的系统建模中较为适用。本文主要讨论三相对称MMC系统动态相量建模仿真，但动态相量法的应用并不局限在三相对称系统，本文结论可推广到三相不对称系统中。

2 MMC建模

2.1 MMC基本结构

图1给出了MMC主电路及其子模块的拓扑。MMC每相的上、下桥臂分别由N个子模块（Sub-Module，SM）和1个串联电抗器构成，SM内部包含1个电容和1个由IGBT和反并联二极管组成的半H桥。SM有3种基本状态：投入、切断和开路。分别对应于上 IGBT和下 IGBT的开通或关断。其中投入状态对应的是上开、下关，切除状态对应的是上关、下开，上、下管全部关断时电路闭锁，对外等效为开路。

2.2 MMC开关模型

三相对称系统以j(j=a,b,c)相为例，单个子模块的开关函数模型为

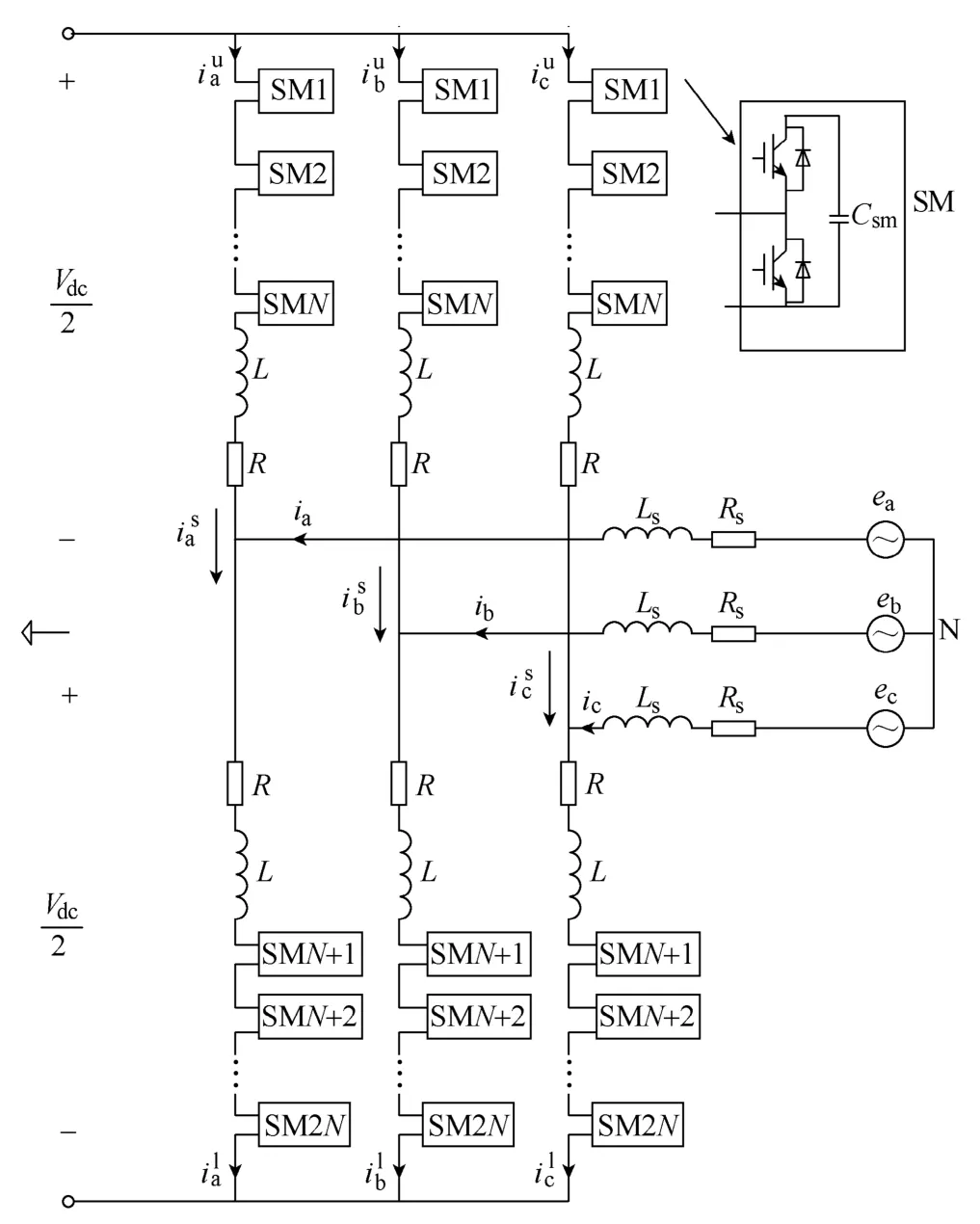
图1 MMC主电路及子模块拓扑Fig.1 Main circuit of MMC and topology of submodule

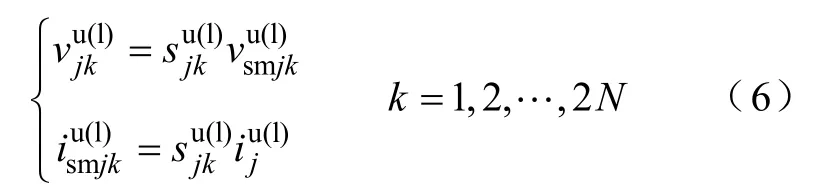
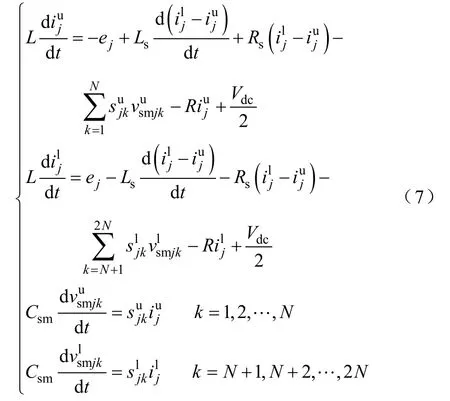
为了降低方程阶数，考虑合理的近似[13]，认为桥臂内子模块间均压效果良好[13]，即、。

定义上、下桥臂开关函数

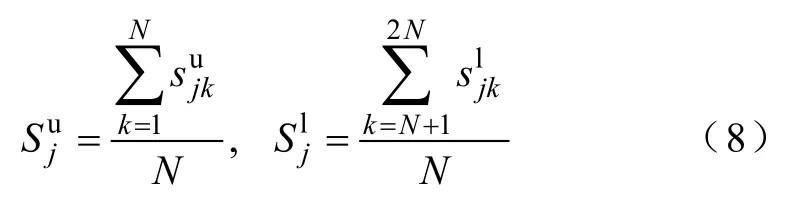
为了便于分析MMC内外部电压、电流特性，将上、下桥臂方程等式两边分别作差及作和，得到新的变量为

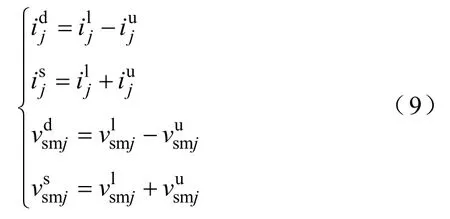
在三相对称调制下，考虑开关函数为直流分量和基频分量的叠加，，一般情况下，上桥臂和下桥臂的功率单元对称互补投入，投入总模块数为N，则Sdc=1、Sj=1/2Msin(ω t+δ)，M、δ分别为调制比和移相角[19-21]。

用上、下桥臂电流和/差与子模块电压和/差表示的MMC开关函数模型为

2.3 MMC动态相量模型

根据式（10），在三相对称的情况下，以j相为例，利用动态相量微分性质，推导MMC换流器动态相量模型为

式中，D为微分算子。

从时域模型式（10）得到式（12）所示的1 0阶非线性、大信号动态相量模型。该模型系统化地考虑了交流侧基波、直流侧直流及二倍频分量，计算精度和速度不受模块数量的限制，适用于超大规模MMC仿真。求解式（12）状态方程得到和的1阶动态相量及和的0阶和2阶动态相量，根据式（1）将各阶动态相量合并，即可完整表征状态变量[22-24]、、和。

3 仿真验证

依据式（12）的动态相量状态方程在Matlab中编写M文件，求解上述10阶状态方程，得到10个状态变量的值。进行如式（13）～式（16）所示的计算，得到、、和的时域表达式，即可得到MMC动态相量模型。其中MMC换流器参数见表 1。为验证 MMC动态相量建模的准确性和高效性，将动态相量模型得到的仿真结果和仿真耗时与Matlab/Simulink中建立的相同参数下的MMC电磁暂态模型进行比较。

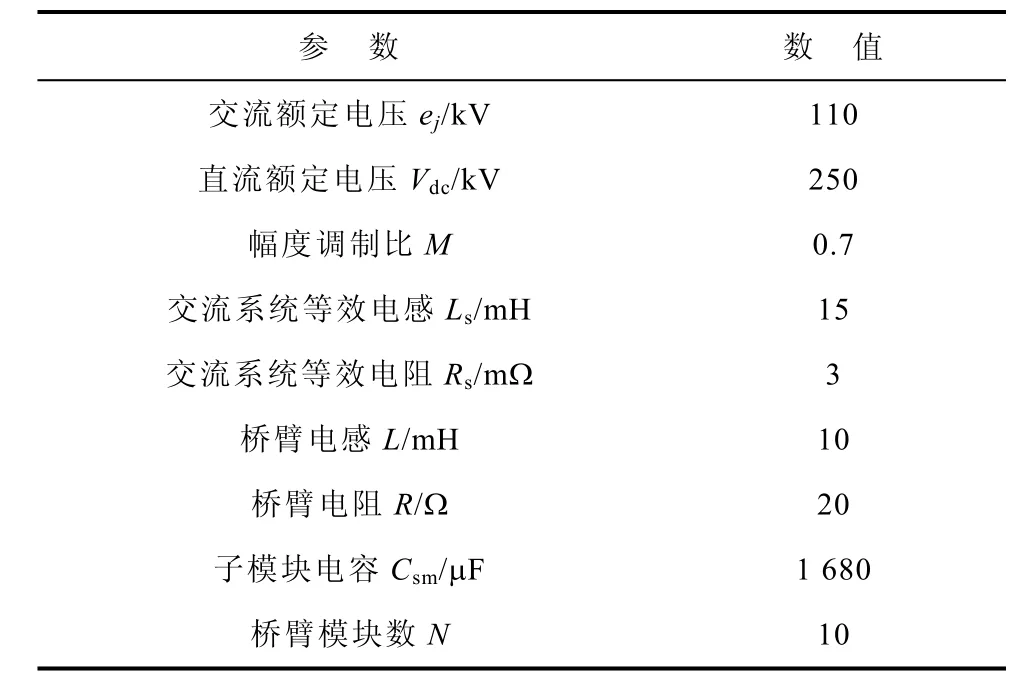
表1 系统参数Tab.1 System parameters

图2 MMC a相交流侧输出电流Fig.2 AC current of MMC phase a

图3 MMC a相桥臂环流Fig.3 Circuiting current of MMC phase a

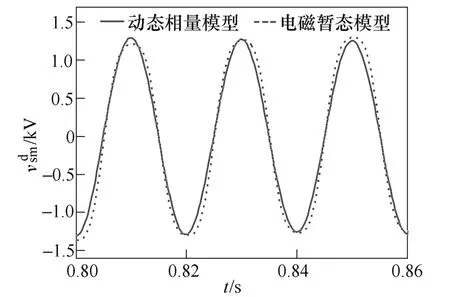
图4 MMC a相上下桥臂子模块电压差Fig.4 Voltage difference of MMC phase a upper and lower arms

为了进一步验证 MMC动态相量模型的准确性，对稳态情况下两种模型中换流器2次环流的幅值进行对比，如表2所示，可见两者误差较小。

为进行暂态运行情况的对比验证，在t=1.0s时设置换流站交流出口三相金属性短路故障，t=1.1s时故障切除，两种模型的有功功率P和无功功率Q的波形对比如图 6、图 7所示，可见暂态过程中动态相量模型和电磁暂态模型的波形比较吻合，存在一些细微的差别，主要原因应是电磁暂态模型考虑了更高次的谐波分量作用。

图5 MMC a相上下桥臂子模块电压和Fig.5 Voltage sum of MMC phase a upper and lower arms

表2 动态相量与电磁暂态模型2次环流（幅值）对比Tab.2 Secondary circulating current comparison of thedynamic phasor model and electromagnetic model

图6 MMC交流侧有功功率Fig.6 Active power of MMC AC side

图7 MMC交流侧无功功率Fig.7 Reactive power of MMC AC side

此外，表3列出了动态相量模型和电磁暂态模型仿真耗时的对比。两种模型均在Matlab中采用变步长的ode45解法进行0～5s的仿真。动态相量模型的仿真耗时远少于电磁暂态模型，证明了动态相量模型的高效性。

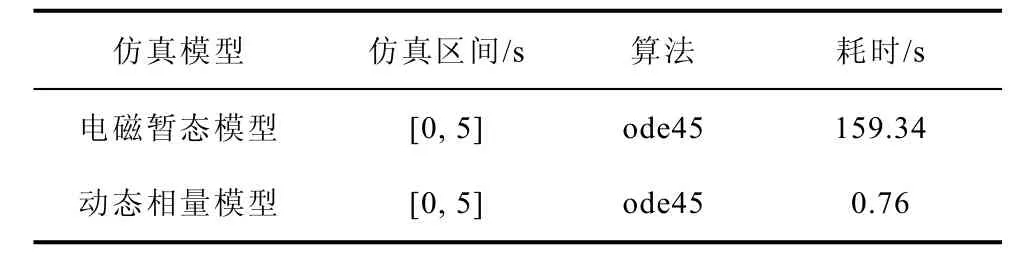
表3 动态相量与电磁暂态模型所用仿真时间对比Tab.3 Simulation time comparison of the dynamic phasor model and electromagnetic model

4 结论

本文在MMC开关函数模型的基础上建立了动态相量模型，并利用Matlab编程实现。通过与应用Matlab/Simulink仿真软件得到的电磁暂态模型仿真结果进行对比，验证了所建模型的正确性，并得到以下结论：

1）所建动态相量模型可较好地刻画MMC的交直流侧电压、电流特征，根据精度要求选取合适的阶次，可以准确得到交流侧电压、电流和包括2次环流在内的直流侧电压、电流特性，继而得到完整的上、下桥臂电压、电流特性。在稳态和暂态情况下，该动态相量模型均适用于MMC换流器内外部特性分析。

2）所建MMC动态相量模型缩短了运算时间，提高了仿真效率，适用于超大规模MMC建模。

[1] 郭捷,江道灼,周月宾,等.交直流侧电流分别可控的模块化多电平换流器控制方法[J].电力系统自动化,2011,35(7):42-47.

Guo Jie,Jiang Daozhuo,Zhou Yuebin,et al.AC and DC current hybrid control strategy for modular multilevel converter[J].Automation of Electric Power Systems,2011,35(7):42-47.

[2] 管敏渊,徐政.模块化多电平换流器型直流输电的建模与控制[J].电力系统自动化,2010,34(19):64-68.

Guan Minyuan,Xu Zheng.Modeling and control of modular multilevel converter in HVDC transmission[J].Automation of Electric Power Systems,2010,34(19):64-68.

[3] 许建中,赵成勇,刘文静.超大规模 MMC电磁暂态仿真提速模型[J].中国电机工程学报,2013,33(10):114-120,11.

Xu Jianzhong,Zhao Chengyong,Liu Wenjing.Accelerated model of ultra-large scale MMC in electromagnetic transient simulations[J].Proceedings of the CSEE,2013,33(10):114-120,11.

[4] Liu S,Xu Z,Hua W,et al.Electromechanical transient modeling of modular multilevel converter based multi-terminal HVDC systems[J].IEEE Transactions on Power Systems,2014,29(1):72-83.

[5] 王姗姗,周孝信,汤广福,等.模块化多电平电压源换流器的数学模型[J].中国电机工程学报,2011,31(24):1-8.

Wang Shanshan,Zhou Xiaoxin,Tang Guangfu,et al.Modeling of modular multi-level voltage source converter[J].Proceedings of the CSEE,2011,31(24):1-8.

[6] Chen B,Chen Y,Tian C,et al.Analysis and Suppression of circulating harmonic currents in a modular multilevel converter considering the impact of dead time[J].IEEE Transactions on Power Electronics,2015,30(7):3542-3552.

[7] 曾正,赵荣祥,杨欢.含逆变器的微电网动态相量模型[J].中国电机工程学报,2012,32(10):65-71.

Zeng Zheng,Zhao Rongxiang,Yang Huan.Dynamic phasors model of micro-grid with grid-connected inverters[J].Proceedings of the CSEE,2012,32(10):65-71.

[8] Deore S R,Darji P B,Kulkarni A M.Dynamic phasor modeling of modular multi-level converters[C]// 7th IEEE International Conference on Industrial and Information Systems(ICIIS),Chennai,India,2012:1-6.

[9] 潘武略,徐政,张静.不对称运行条件下 VSCHVDC动态相量建模[J].高电压技术,2009,35(7):1705-1710.

Pan Wulue,Xu Zheng,Zhang Jing.Dynamic phasors modeling of the VSC-HVDC under unbalanced conditions[J].High Voltage Engineering,2009,35(7):1705-1710.

[10] 钟庆,黄凯,王钢,等.不对称三相电压下电压源型换流器谐波分析与抑制策略[J].电力系统自动化,2014,38(4):79-85.

Zhong Qing,Huang Kai,Wang Gang,et al.Harmonic analysis and elimination strategy for voltage source converter under unbalance three-phase voltage[J].Automation of Electric Power Systems,2014,38(4):79-85.

[11] 王钢,李志铿,李海锋,等.交直流系统的换流器动态相量模型[J].中国电机工程学报,2010,30(1):59-64.

Wang Gang,Li Zhikeng,Li Haifeng,et al.Dynamic phasor model of the converter of the AC/DC system[J].Proceedings of the CSEE,2010,30(1):59-64.

[12] Saad H,Peralta J,Dennetiere S,et al.Dynamic averaged and simplified models for MMC-based HVDC transmission systems[J].IEEE Transactions on Power Delivery,2013,28(3):1723-1730.

[13] 郭捷.模块化多电平换流器在 HVDC应用的若干关键问题研究[D].杭州:浙江大学,2013.

[14] 张建坡,赵成勇.模块化多电平换流器环流及抑制策略研究[J].电工技术学报,2013,28(10):328-336.

Zhang Jianpo,Zhao Chengyong.Research on circulation current and suppressing strategy of modular multilevel converter[J].Transactions of China Electrotechnical Society,2013,28(10):328-336.

[15] 肖晃庆,徐政,薛英林,等.模块化多电平换流器谐波特性解析分析[J].中国科学:技术科学,2013,43(11):1272-1280.

Xiao Huangqing,Xu Zheng,Xue Yinglin,et al.Theoretical analysis of the harmonic characteristics of modular multilevel converters[J].Scientia Sinica:Technologica,2013,43(11):1272-1280.

[16] 雷鸣,李耀华,葛琼璇,等.一种新型单桥臂电感模块化多电平变流器及其控制方法[J].电工技术学报,2014,29(2):231-238.

Lei Ming,Li Yaohua,Ge Qiongxuan,et al.A new modular multilevel converter with single arm inductor and its control strategies[J].Transactions of China Electrotechnical Society,2014,29(2):231-238.

[17] 邓旭,王东举,沈扬,等.舟山多端柔性直流输电工程换流站内部暂态过电压[J].电力系统保护与控制,2013,41(18):111-119.

Deng Xu,Wang Dongju,Shen Yang,et al.Research on transient overvoltage for converter station of Zhoushan multi-terminal VSC-HVDC project[J].Power System Protection and Control,2013,41(18):111-119.

[18] Ilves K,Antonopoulos A,Norrga S,et al.Steady-state analysis of interaction between harmonic components of arm and line quantities of modular multilevel converters[J].IEEE Transactions on Power Electronics,2012,27(1):57-68.

[19] 管敏渊,徐政.向无源网络供电的MMC型直流输电系统建模与控制[J].电工技术学报,2013,28(2):255-263.

Guan Minyuan,Xu Zheng.Modeling and control of modular multilevel converter based VSC-HVDC system connected to passive networks[J].Transactions of China Electrotechnical Society,2013,28(2):255-263.

[20] 杨晓峰,郑琼林.基于 MMC环流模型的通用环流抑制策略[J].中国电机工程学报,2012,32(18):59-65,178.

Yang Xiaofeng,Zheng Qionglin.A novel universal circulating current suppressing strategy based on the MMC circulating current model[J].Proceedings of the CSEE,2012,32(18):59-65,178.

[21] Gnanarathna U N,Gole A M,Jayasinghe R P,Efficient modeling of modular multilevel HVDC converters(MMC)on electromagnetic transient simulation programs[J].IEEE Transactions on Power Delivery,2011,26(1):316-324.

[22] 薛英林,徐政.基于箝位双子模块的MMC-HVDC起动控制策略[J].电力系统保护与控制,2013,41(11):1-7.

Xue Yinglin,Xu Zheng.Start control for the MMCHVDC system based on clamp double submodule[J].Power System Protection and Control,2013,41(11):1-7.

[23] 蒋冠前,李志勇,杨慧霞,等.柔性直流输电系统拓扑结构研究综述[J].电力系统保护与控制,2015,43(15):145-153.

Jiang Guanqian,Li Zhiyong,Yang Huixia,et al.Research review on topological structure of flexible HVDC system[J].Power System Protection and Control,2015,43(15):145-153.

[24] 江政昕,李广凯,王鸿雁,等.模块化多电平换流器直流输电稳态仿真分析[J].电气技术,2011,12(8):5-9.

Jiang Zhengxin,Li Guangkai,Wang Hongyan,et al.Simulation and analysis of HVDC power transmission steady state based modular multilevel voltage source converter[J].Electrical Engineering,2011,12(8):5-9.