考虑漏磁效应的新型磁控可调电抗器的磁路建模和特性

林克曼 李 念 林明耀 万秋兰

（东南大学电气工程学院 南京 210096）

1 引言

近年来，随着我国特高压交直流输电技术及其工程应用取得突破，对连续可调的可控电抗器的需求日益迫切。现阶段电网中得到广泛应用的相控可调电抗器（Thyristor Controller Reactor，TCR）[1]，其反应速度快，技术较成熟，但是价格昂贵，谐波污染较严重，且受到绝缘材料性能等限制，难以应用于高压输电系统中。磁控可调电抗器[2-7]，因具有控制灵活，运行损耗低，可实现电抗的连续调节等优点，在高电压和特高压输电系统中具有良好的应用前景，受到广泛关注。研究表明，可控电抗器具有电网无功补偿、限制操作过电压、提高系统的输电能力和改善电能质量等功能[8-10]。文献[11]研究了可控高压电抗器在西北电网的应用，指出电抗器对电网具有良好的电压支撑作用，在一定程度上可降低网损，并通过抑制电压波动，提高了系统稳定性。文献[12]将可调电抗器安装于特高压输电系统的母线上，以解决长距离重载线路限制过电压和无功调节的矛盾。文献[13]提出了一种将可控电控器与变压器、电容器等元件配合，实现输电线路有功和无功潮流解耦控制的方法。

通常，磁控可调电抗器分为两种类型：正交可控电抗器[14]和饱和电抗器[15,16]。两者的主要区别在于控制绕组的位置不同，由直流控制绕组产生的直流磁通和交流绕组产生的交流磁通的路径不同。正交可控电控器的直流磁通正交于交流磁通，饱和电抗器的直流磁通与交流磁通相平行。文献[17]通过对正交磁通和平行磁通两种磁通分布进行分析对比发现，基于铁心正交磁化原理的正交可控电抗器，其直流控制磁场与交流磁场相互正交，相互正交的磁场赋予电抗器良好的线性电抗特性，但是这类电抗值的调节范围受到限制；平行磁场则扩大了饱和电抗器的调节范围，但是其控制特性逊于正交可控电控器。为了结合这两种可调电抗器的优点，同时改进它们的缺点，本文设计研究了一种基于磁放大原理的新型可调电抗器，通过在主铁心中部设置气隙，增加电抗器的调节范围，同时改善由于铁心材料引起的电抗器的非线性特性，获得良好的控制特性；通过调整交、直流绕组的位置，减小电抗器达到饱和所需的直流控制电流，节省了能源。

本文在分析新型磁控式可调电抗器工作机理和控制特性的基础上，基于三维有限元法仿真计算了其磁场分布，建立了考虑漏磁效应的磁控可调电抗器的等效磁路和数学模型，进行设计计算，并通过与样机试验数据的比较分析，验证了所建立模型的正确性。

2 新型SCCR 的基本结构和工作原理

2.1 新型SCCR 的基本结构

图1 为新型SCCR 的单相拓扑结构示意图。该可调电抗器的交流绕组总匝数为NAC，分为匝数相等的上、下两个部分绕在中间主铁心柱上，串联后与电网相连，又称工作绕组。中间铁心柱上开有气隙。直流绕组作为控制绕组，一分为二对称绕在两侧铁心柱上，每侧各有匝，串联后与直流电源相连，形成直流闭合回路。

图1 新型磁控饱和可调电抗器结构图Fig.1 Schematic diagram of new type of SCCR topology

当控制直流绕组中电流为零时，铁心中只有交流磁通ΦAC流过，两侧铁心柱中的磁通方向相反。直流绕组通入直流电流，两侧铁心中产生直流磁通ΦDC，ΦDC不通过中间铁心柱而是沿外围铁心顺时针流通形成闭合回路。在交流电源的正、负半周，两侧铁心中直流磁通和交流磁通叠加后使一侧磁通增强，另一侧削弱。相比较传统两柱铁心电抗器，新型磁控可调电抗器具有下列优点[18]：

（1）通过在中间铁心中插入气隙，增大了可控电抗器的电抗调节范围，改善了磁饱和式可调电抗器的非线性磁化特性，使可调电抗器获得平滑线性的控制特性。

（2）气隙位于中间铁心柱，直流磁通流经外围铁心，气隙对直流磁路不产生影响，这解决了气隙引起直流励磁电流增大的问题，降低了对直流偏磁电源容量的要求。

（3）交流磁通匝链两侧直流绕组感应相位相反的交流电势，但由于两直流绕组相串联，感应的交流电势相互抵消，对直流电源几无影响。

2.2 新型SCCR 的工作原理

直流绕组电流产生直流偏磁磁通，由于铁心材料磁化曲线的非线性及饱和影响，不同直流偏磁下交流电流产生的在两侧铁心柱中的交流磁通幅值不同。当直流偏磁绕组中电流为零时，电抗器相当于变压器空载运行，交流绕组的电抗最大。根据磁路的基尔霍夫第一定律，流入磁路节点的磁通代数和等于零，即中间铁心柱磁通等于左侧铁心磁通与右侧铁心磁通的代数和。当直流偏磁绕组中电流不等于零时，在交流绕组的一个工作周期，由于直流和交流磁通的叠加作用，使得左右两个铁心中磁通既有直流又有交流成分。在半个周期内，左右铁心中一个铁心中的交直流磁通相加，另一个铁心中的交直流磁通相减，另外半个周期则相反。因此，在相同的交流工作电流下，调节直流偏磁电流，就可以调节两侧铁心中叠加的交流磁通幅值，也即调节交流绕组中的等效磁通幅值，改变磁路的饱和程度，控制电抗器的等效电抗值。

图2 所示为新型磁控可调电抗器的工作原理图。图中f1、f2分别为两侧铁心柱中交、直流磁动势的叠加波形，φ1、φ2分别为两侧铁心柱中磁通波形，φ3为φ1、φ2合成后中间铁心柱中的波形。由于铁心材料磁化曲线的饱和特性，两侧铁心中的磁通波形正负半周不对称，且都有一定程度的畸变，但两者叠加后，即交流绕组匝链的磁通波形有较好的正弦度。

图2 新型可调电抗器工作原理Fig.2 Operation principle of new type of SCCR

直流绕组中偏磁电流为零时，可调电抗器等同于空载电抗器，等效电抗最大；直流绕组流过最大偏磁电流时，可调电抗器等同于饱和电抗器，等效电抗最小，接近于零。调节直流偏磁电流，就可以连续平滑的调节可调电抗器的等效电抗值。

3 考虑漏磁效应的新型SCCR 等效磁路和数学模型

3.1 有限元仿真

为验证新型SCCR 的设计方法和测试其电气性能，设计制作了一台33kVA/120A 电抗器样机，表1 为其结构参数。利用Maxwell 软件建立单相可调电抗器的有限元模型，图3 为饱和电抗器三维有限元模型及剖分网格。为观察不同电流时可调电抗器铁心磁场分布的变化规律，分两种情况给交流和直流绕组施加电流：①交流绕组中工作电流不变，调节直流绕组中偏磁电流，计算铁心磁场分布；②直流绕组中偏磁电流不变，交流绕组电流一个周期正半周和负半周的铁心磁场分布。

表1 新型SCCR 样机结构参数Tab.1 Parameters of prototype

图3 可调电抗器有限元模型Fig.3 Finite element model of SCCR

设交流电流达到峰值iAC=170A，不同直流偏磁电流下铁心中的磁场分布如图4 所示。直流偏磁不同，外围磁路的饱和程度不同。由图4a 可知，直流偏磁电流为零时，左右铁心中磁通相同；对比图4a、4b 可知，施加直流偏磁，直流磁路的磁通增大，磁路饱和程度加剧，中间铁心柱的磁通较小，但交流磁回路的饱和程度增强，电抗减小，实现由直流偏磁电流调节电抗器电抗值的目的。

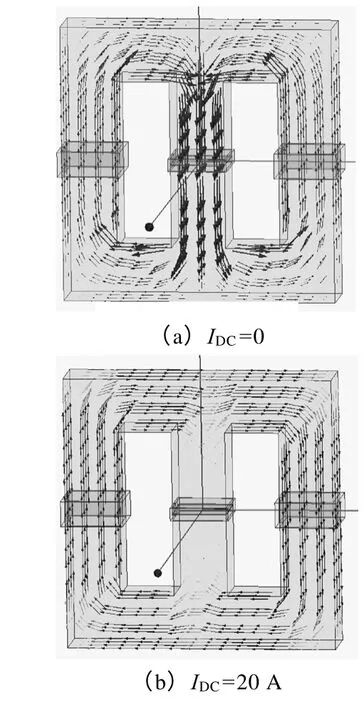
图4 不同直流偏磁电流下的磁场分布Fig.4 Magnetic field distribution in different DC currents

图5 所示为电抗器交流电流为零和正、负半周峰值时，电抗器铁心的磁通密度大小和方向。由图5b 可知，在交流电流的正半周，右侧铁心柱上直流磁通和交流磁通相累加，左侧铁心柱上直流磁通和交流磁通相减；图5c 对应交流电流的负半周，直流和交流磁通的叠加作用和结果相反。中间铁心柱仅通过交流磁通，并不通过直流磁通，图2 中曲线φ3也说明了这一点。

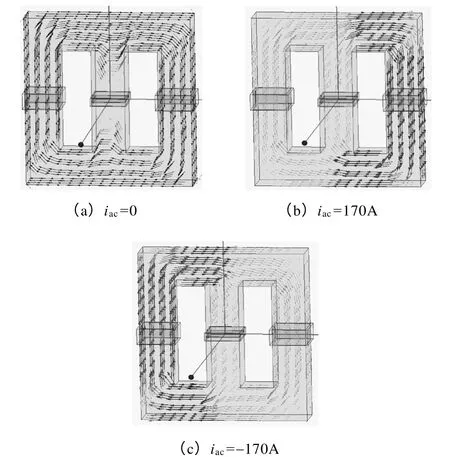
图5 不同交流电流下的磁场分布Fig.5 Magnetic field distribution in different AC currents

3.2 考虑漏磁效应的SCCR 等效磁路模型和数学建模

3.2.1 假设条件和磁场划分

利用Maxwell 有限元分析软件，得到图6 所示的计及漏磁影响的新型磁控可调电抗器的磁场分布。

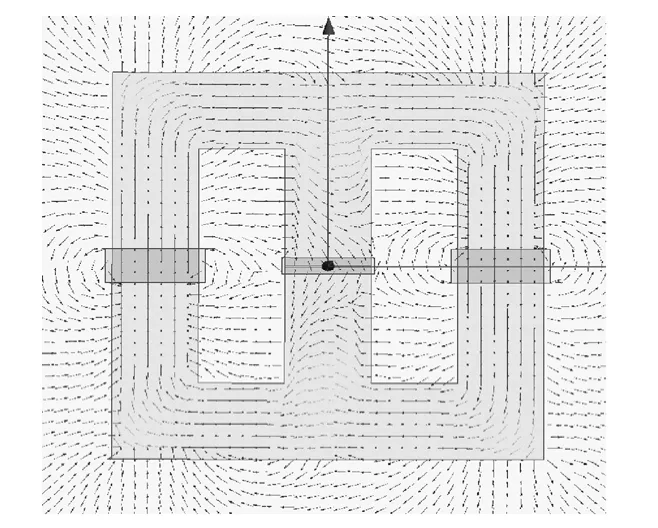
图6 考虑漏磁效应的电抗器磁场分布Fig.6 Magnetic field distribution of SCCR withflux leakage effect

采用等效磁路法计算电抗器的电抗，为简化起见，作出如下假设：

（1）对于一段场强H 变化的铁心，假设它的场强H 沿平均长度方向的变化是均匀的，即取磁路中变化的磁场强度算术平均值作为该段磁路的磁场强度。

（2）忽略棱角处的漏磁通，只考虑铁心侧面漏磁，这样将电抗器漏磁场划分为典型的具有简单几何形状的磁通管。

（3）各媒质均为各向同性材料，且忽略时变场频率的影响。

基于以上假设，根据图6 所示磁场分布，将电抗器磁路划分为如图7 所示的铁心主磁路和不同漏磁路径。其中，电抗器左、右铁心漏磁场以半圆形、半圆环磁通管表示，它们与中间铁心柱之间表示为矩形磁通管，左右铁心柱的内侧漏磁场表示为半圆形磁通管。

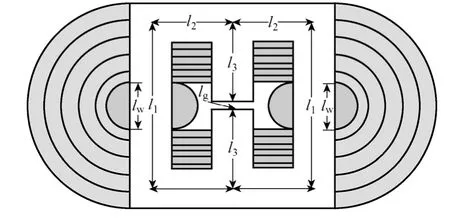
图7 新型SCCR 磁场区域划分Fig.7 Magnetic field partition of new type of SCCR

3.2.2 主磁路磁导计算

根据电抗器铁心磁路划分，将交直流绕组作为集总参数处理，每段铁心磁导也作为集总参数元件来处理。交直流绕组提供的磁动势为

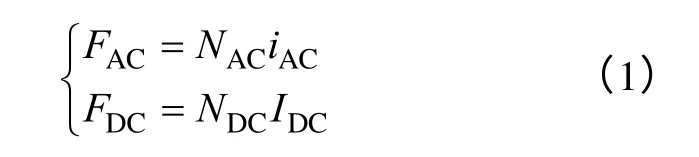
任意一段铁心的磁导按下式计算

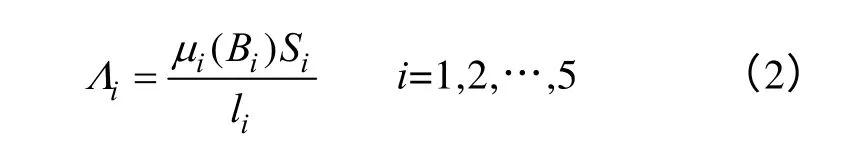
式中 li，Si和μi(Bi)——第i 段铁心的长度、截面积和磁导率。

铁心材料磁化曲线的非线性，使其磁导率μ i 随着磁路饱和程度的变化而变化，即μ i 是Bi的函数。由于交直流磁通的不对称叠加，各对称位置的铁心的磁导不同。

设lg、Sg分别气隙长度和截面积，μ 0 为真空磁导率，气隙磁导为

3.2.3 漏磁导计算

由铁心漏磁场分布可知，漏磁导的计算相对铁心主磁导要复杂得多。采用磁场分割法求解电抗器漏磁导[19]。将铁心表面视作等磁动势面，图8 所示灰色部分为划分的三种典型几何形状的磁通管，磁通管长度为电抗器的截面宽度la。其中，半圆柱体磁通管漏磁导计算公式为

图8 漏磁路径的简化划分Fig.8 Simple division of flux leakage

根据半空心圆柱体磁通管漏磁导计算公式，可得半圆环磁通管的漏磁导为

矩形截面磁通管漏磁导为

3.2.4 磁动势方程

根据以上分析，可得如图9 所示的电抗器等效磁路模型。图9 中，考虑到左、右铁心柱都为立方柱体，它们的漏磁导有如下关系

且令

图9 考虑漏磁效应的等效磁路模型Fig.9 Equivalent magnetic circuit model with flux leakage effect

根据等效磁路模型，以节点z 为参考磁位点，建立节点磁动势方程见式（9）。

简写为

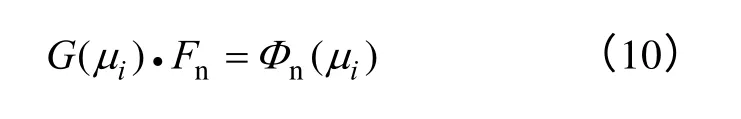
求解磁动势方程（9），得到中间铁心柱磁通ΦAC，由式（11）计算中间铁心柱工作绕组的电感为

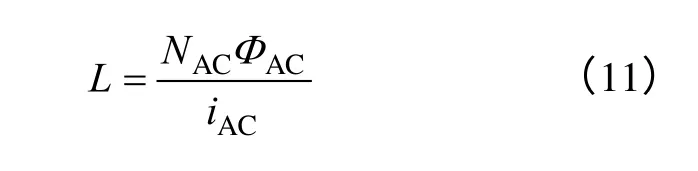
改变直流偏磁电流和交流工作电流，可得到电抗器控制特性。

4 实验研究及结果分析

4.1 试验样机参数

为了验证3.2 中所建立的等效磁路模型的正确性，对设计和研究的新型磁控可调电抗器样机进行测试，实验平台如图10 所示。

图10 样机试验接线图Fig.10 Schematic of the SCCR test circuit

实验直流电源由一个IGBT 可控整流器及PWM控制器组成，为直流绕组提供偏磁电流，试验中，直流电流的调节范围为0～200A。可调交流负载与电抗器工作绕组串联，接至交流电源。控制直流偏磁电流为IDC=0，电抗最大，增大直流偏磁电流为IDC=200A，改变交流负载，测得当工作电流iAC=120A 时，电抗最小。可调电抗器的测试参数见表2。

表2 新型磁控可调电抗器参数Tab.2 Parameters of new type of SCCR

4.2 仿真结果分析

调节交流电流为120A，不同直流偏磁电流下新型SCCR 电抗X 的实测和仿真结果见表3。电流较大时，铁心的漏磁较严重。由表可知，考虑漏磁效应后，采用等效磁路法的仿真结果更接近于实测值。

表3 仿真结果和测试结果比较Tab.3 Comparison of simulation with test results

图11 所示为交流工作电流120A 时，仿真得到的新型磁控可调电抗器控制特性曲线，并与样机测试结果进行了比较。由图可知，新型SCCR 可实现电抗的连续平滑调节。当直流偏磁电流小于20A 时，随直流电流的增大，铁心磁路饱和程度急剧变化，电抗器电抗快速减小；当直流偏磁电流大于20A，直流偏磁电流增加时，交流铁心磁路饱和程度变化较为平缓，磁导率减小缓慢，电抗器的电抗线性下降；当直流偏磁电流大于150A 时，电抗值几乎不随直流偏磁电流改变。

图11 iAC=120A 控制特性仿真与样机测试结果Fig.11 Control characteristics of SCCR by calculation and testing for iAC=120A

比较仿真计算与测试结果发现，在控制特性中段，计算结果与样机测试数据存在偏差，产生这些偏差的主要原因，是在建立等效磁路模型时，将电抗器铁心表面视作等磁动势面，导致计算的直流偏磁引起的外围铁心的饱和效应与实际情况的差异所致。直流偏磁电流较小或较大时，采用等效磁路法计算得到的控制特性曲线和测试结果相同。因此，论文给出的方法可以用于快速计算新型磁控可调电抗器的控制特性。

5 结论

本文设计和研究了一种在中间铁心设置气隙的新型SCCR。基于对该电抗器的三维有限元分析，将漏磁区域等效成不同形状的磁通管，建立了考虑漏磁效应的可调电抗器等效磁路模型和相应的数学模型，计算了不同负载和直流偏磁电流下电抗器的电抗，制作了样机，进行了实验研究。理论计算和实验测试结果表明：通过在电抗器交流绕组的中间铁心设置气隙，实现了可调电抗器平滑线性的控制特性，增大了电抗调节范围，气隙对直流磁路不产生影响，解决了设置气隙增大直流偏磁电源容量的问题；当直流偏磁电流小于20A，电抗器电抗随直流电流的增大急剧变化，当直流偏磁电流大于150A，电抗几乎不随直流偏磁电流变化；仿真计算与实测控制特性较为吻合，说明了论文提出的等效磁路法的有效性，这为新型磁控可调电抗器的快速优化设计和应用奠定了基础。

[1] Mathur R M,Varma R K.Thyristor-based FACTS controllers for electrical transmission systems[M].New Jersey:John Wiley & Sons,2002.

[2] 李达义,陈乔夫.基于磁通可控的可调电抗器的新原理[J].中国电机工程学报,2003,23(2):116-120.

Li Dayi,Chen Qiaofu.A novel principle of adjustable reactor based on magnetic flux controllable[J].Proceedings of the CSEE,2003,23(2):116-120.

[3] 张宇,陈乔夫,程路,等.基于磁通补偿的高压大容量可控电抗器[J].电工技术学报,2009,24(3):93-98.

Zhang Yu,Chen Qiaofu,Cheng Lu,et al.A highvoltage and large-capacity controllable reactor based on magnetic flux compensating[J].Transactions of China Electrotechnical Society,2009,24(3):93-98.

[4] 宋江保,王贺萍,张战永,等.三相磁阀式可控电抗器的分析研究[J].电力系统保护与控制,2009,37(23):20-22.

Song Jiangbao,Wang Heping,Zhang Zhanyong,et al.Analytical study of controllable reactor based on three-phase magnetism valve type[J].Power System Protection and Control,2009,37(23):20-22.

[5] 陈绪轩,田翠华,陈柏超,等.多级饱和磁阀式可控电抗器谐波分析数学模型[J].电工技术学报,2011,26(3):57-64.

Chen Xuxuan,Tian Cuihua,Chen Baichao,et al.Mathematical model for harmonics analysis of the multi-stage saturable magnetic-valve controllable reactor[J].Transactions of China Electrotechnical Society,2011,26(3):57-64.

[6] Wass T,Hornfeldt S,Valdemarsson S.Magnetic circuit for a controllable reactor[J].IEEE Transactions on Magnetics,2006,42(9):2196-2200.

[7] 刘仁,赵国生,王欢,等.三相磁阀式可控电抗器的特性仿真分析[J].电力系统保护与控制,2011,39(7):110-114.

Liu Ren,Zhao Guosheng,Wang Huan,et al.Characteristic simulation analysis of three-phase magnetic valve type controlled reactor[J].Power System Protection and Control,2011,39(7):110-114.

[8] 杨民生,王耀南,欧阳红林,等.基于可控电抗器的无接触电能传输系统动态补偿[J].电工技术学报,2009,24(5):183-189.

Yang Minsheng,Wang Yaonan,Ouyang Honglin,et al.Dynamic compensation of contact-less power transmission system based on controlled reactor[J].Transactions of China Electrotechnical Society,2009,24(5):183-189.

[9] 周沛洪,何慧雯,戴敏,等.可控高抗在1000kV 交流紧凑型输电线路中的应用[J].高电压技术,2011,37(8):1832-1842.

Zhou Peihong,He Huiwen,Dai Min,et al.Application of controllable reactors to 1000kV AC compact transmission line[J].High Voltage Engineering,2011,37(8):1832-1842.

[10] 魏云冰,李涛,张国亮,等.基于瞬时无功功率理论的磁控电抗器控制方法[J].电力系统保护与控制,2011,39(22):117-121.

Wei Yunbing,Li Tao,Zhang Guoliang,et al.A control method for the magnetic-valve controllable reactor based on instantaneous reactive power theory[J].Power System Protection and Control,2011,39(22):117-121.

[11] 潘雄,丁新良,黄明良,等.可控高压电抗器应用于西北750kV 电网的仿真分析[J].电力系统自动化,2008,31(22):104-107.

Pan Xiong,Ding Xinliang,Huang Mingliang,et al.Simulation analysis on application of controllable reactors in 750kV northwest China power grid[J].Automation of Electric Power Systems,2008,31(22):104-107.

[12] 周勤勇,郭强,卜广全,等.可控电抗器在我国超/特高压电网中的应用[J].中国电机工程学报,2007,27(7):1-6.

Zhou Qinyong,Guo Qiang,Bu Guangquan,et al.Application of controllable reactors in China's power grid at extra and ultra voltage level[J].Proceedings of the CSEE,2007,27(7):1-6.

[13] 江渝,王恒,郑群英,等.一种可调电感控制线路潮流的方法[J].电工技术学报,2011,26(9):196-200.

Jiang Yu,Wang Heng,Zheng Qunying,et al.Control method of power flow with adjustable inductor[J].Transactions of China Electrotechnical Society,2011,26(9):196-200.

[14] Hong H,Zhang J,Song M,et al.Magnetization study on a new type of orthogonally configured magnetic core structure and its potential application to superconducting controllable reactors[J].IEEE Transactions on Applied Superconductivity,2013,23(3):5001004.

[15] 田铭兴,励庆孚.磁饱和式可控电抗器的等效电路及仿真分析[J].电工技术学报,2003,18(6):64-67.

Tian Mingxing,Li Qingfu.An equivalent circuit and simulation analysis of magnetically-saturated controllable reactors[J].Transactions of China Electrotechnical Society,2003,18(6):64-67.

[16] Tian M,Li Q,Li Q.A controllable reactor of transformer type[J].IEEE Transactions on Power Delivery,2004,19(4):1718-1726.

[17] 朱宝森,关毅,陈庆国,等.正交磁化可控电抗器的设计与特性分析[J].电机与控制学报,2012,16(5):26-32.

Zhu Baosen,Guan Yi,Chen Qingguo,et al.Design and characteristics analysis of orthogonal magnetization controllable reactor[J].Electric Machines and Control,2012,16(5):26-32.

[18] Dimitrovski A,Li Z,Ozpineci B.Applications of saturable-core reactors(SCR) in power systems[C].IEEE PES T&D Conference and Exposition,2014:1-5.

[19] 郑永成,王洋,何建国,等.基于磁场分割的磁导计算与磁路设计[J].机械与电子,2006(7):11-13.

Zheng Yongcheng,Wang Yang,He Jianguo,et al.Permeance calculation and magnetic circuit design based on magnetic field division[J].Machinery and Electronics,2006(7):11-13.