基于改进增益阻抗实部的配电网电压跌落源定位方法

朱 珂 王怡轩 刘文华

（1.电网智能化调度与控制教育部重点实验室 山东大学 济南 250061 2.东营供电公司 东营 257091）

0 引言

电压跌落是指电压有效值在系统频率下瞬时减小到额定值的10%～90%，其持续时间一般为半个工频周期到数秒[1]。近年来，随着电力系统中敏感性负荷比例的迅速增加及电力用户对电能质量要求的不断提高，电压跌落己成为供电部门和用户最为关心的电能质量问题之一[2,3]。据统计，在用户投诉的电能质量问题中90%是由于电压跌落引起的。引起电压跌落的原因主要有线路短路故障、大型感应电动机起动以及空载变压器投入等。其既有可能发生在用户侧，也有可能发生在系统侧。而电压跌落源的准确定位对于确认电压跌落责任方，进而采取措施提高整个电网的电能质量具有重要意义[4,5]。

针对电压跌落源定位问题，国内外先后开展了大量研究工作[6]。基于扰动功率和扰动能量的定位方法[7]是较常用也是较早出现的一种方法。该方法以扰动源从系统中吸取能量为前提，通过计算电压跌落发生时的扰动功率和扰动能量并根据其符号来判定电压跌落源的位置。该方法的准确性很大程度上取决于扰动功率和扰动能量计算结果的吻合度，后来多位学者又对其进行了改进和完善[8,9]。文献[10]通过在电压跌落发生时从测量点获得的基频电压幅值与功率因数的乘积同基频电流幅值之间的关系，利用最小二乘法拟合直线的斜率来确定电压跌落源的位置。该方法面对非线性负荷下的有效性有待于进一步验证。文献[11]提出借助距离保护中数字式阻抗继电器，基于测量阻抗的大小和相角实现电压跌落源的定位。当跌落源位于辐射型网络中阻抗继电器上游时，该方法存在工作盲区。文献[12]通过对系统参数的在线监测实现电压跌落源定位，其结果有助于对引起电压跌落的责任进行量化。文献[13]提出利用基波正序增益阻抗实部来对电压跌落源进行定位，该方法物理概念明确，对线性和非线性系统均适用。但由于配电网发生的部分非对称性电压跌落引起的正序分量变化很小[14]，使得该方法应用于此类非对称性电压跌落时难以保证定位准确性。文献[15]在对电压跌落源进行辨识的同时，基于跌落源的类型有针对性地对其进行定位，有助于提高定位准确性。

本文针对原有基于增益阻抗实部的电压跌落源定位方法[13]的不足之处，基于电压跌落源的不同类型，提出了一种基于增益阻抗理论的改进型电压跌落源定位方法，并将其应用于国内辐射型配电线路的电压跌落源定位。理论、仿真分析及模拟实验都验证了该方法的有效性。

1 方案原理与理论分析

1.1 增益阻抗的定义

增益阻抗Ze的定义为[13]

式中，Vduring、Iduring为扰动发生时测量点处的相电压和电流；Vpre、Ipre为扰动发生前瞬间测量点处的相电压和电流。

图1 增益阻抗原理图Fig.1 Schematic of incremental impedance

借助图1所示线性系统可对Ze做进一步阐述。其中，M为测量点，ED和EU分别为测量点下游和上游的等效电源，ZD和ZU分别为测量点下游和上游的等效阻抗。

当上游发生扰动时，测量点M处测得的Ze为

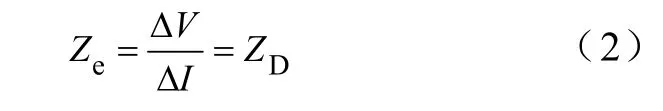
当下游发生扰动时，测量点M处测得的Ze为

由此可以看出，ΔV/ΔI即定义的增益阻抗Ze具有明确的物理概念，如果上游侧发生扰动，它就是下游侧的等效阻抗；如果下游侧发生扰动，它就是上游侧等效阻抗的负值。文献[13]基于这一特性提出了基于增益阻抗实部的电压跌落源定位原理，即利用测量到的基波正序增益阻抗实部的符号来对电压跌落源进行定位。而由于部分非对称性电压跌落（如单相接地故障导致的电压跌落）引起的正序分量变化很小[14]，难以根据故障发生前后正序分量的变化准确计算正序增益阻抗的实部，从而无法对该单相电压跌落源进行准确定位。

除了基波正序阻抗之外，其他各序及各次谐波阻抗同样可以用于电压跌落源的定位。因此虽然文献[13]提出的方法存在不足之处，但由于其具有物理概念明确这一优点，因此如果在对电压跌落源进行初步辨识的基础上，根据跌落源的类型采用相应序分量或谐波阻抗对其进行定位，定位准确性将会得到明显改善。

1.2 基于增益阻抗原理的改进型配电网电压跌落源定位方法

1.2.1各序增益阻抗判据分析

对于图2所示国内10kV辐射型配电系统，各馈线出口端作为能够获得三相电压、电流的典型测量点，其测得的由各序分量构成的增益阻抗从理论上讲都可对电压跌落源进行定位。

图2 简化的国内10kV辐射型配电系统示意图Fig.2 Simplified schematic diagram of domestic 10kV radiation distribution system

（1）正序增益阻抗判据

中性点非有效接地系统发生电压跌落时，在电压跌落源与非电压跌落源所在馈线出口处测得的基波正序增益阻抗

式中，ZL为非电压跌落馈线单相负荷等效阻抗；ZS为母线上游单相系统等效阻抗。

即非电压跌落源所在线路出口处测得的基波正序增益阻抗为其自身单相负荷等效阻抗，呈感性，位于阻抗图第一象限；电压跌落源所在线路出口处测得的基波正序增益阻抗为母线上游单相系统等效阻抗的负值，呈容性，位于第三象限。

（2）零序增益阻抗判据

1）中性点不接地系统。对于中性点不接地系统，当某条馈线发生电压跌落时，忽略线路上的阻抗，其端口根据基波测得的电压跌落源与非电压跌落源所在线路的零序增益阻抗分别为

式中，Cus为非电压跌落线路单相对地零序电容；Cs为电压跌落源所在线路的单相对地零序电容；C∑为所有馈线单相对地零序电容之和。

可见电压跌落源所在线路零序增益阻抗位于第二象限，显感性；非电压跌落源所在线路零序增益阻抗位于第四象限，显容性。

2）中性点谐振接地系统。当中性点谐振接地系统发生单相接地故障时，由于消弧线圈的电感值Lx是按照基波整定的，因此无法利用基波零序增益阻抗来对谐振接地系统中的电压跌落源进行有效定位。如果借助系统中含量较高的5次谐波计算零序增益阻抗，则有

通过式（6）可知，利用5次谐波算得的电压跌落源所在馈线出口处的零序增益阻抗仍呈感性，而非电压跌落源所在线路的零序增益阻抗仍呈容性，所以可以用根据5次谐波算得的零序增益阻抗作为谐振接地系统的电压跌落源定位依据。

需要指出的是，当电压跌落来自 10kV上游更高电压等级时，各 10kV馈线出口测得的增益阻抗均会显示跌落源位于其上游，由此可以判定电压跌落来自上游更高电压等级。

上述推导出的各序分量增益阻抗电压跌落源判据所适用的电压跌落源类型如下：①基于正序增益阻抗理论的电压跌落源定位判据适用于电压跌落发生前后测量点处正序电压、电流分量发生明显变化的跌落源类型，如相间短路故障、电动机起动或投空载变压器引起的电压跌落。②基于零序增益阻抗理论的电压跌落源定位判据适用于电压跌落发生前后测量点处零序电压、电流分量发生明显变化的跌落源类型，如单相接地故障引起的电压跌落。

1.2.2配电变压器电压跌落传递能力分析

随着国内配网的改造升级，部分配电变压器具备了同主站间的通信功能。因此，此类配电变压器380V端口也可作为本课题的典型测量点用于电压跌落源定位。而由于配电变压器自身联结方式等特性，造成部分电压跌落难以通过配电变压器进行有效传递[16]。

（1）380V侧电压跌落传递能力分析

图3为配电线路单相等效电路。其中，ZX为线路阻抗；ZT1、ZT2分别为变压器等效电路的励磁阻抗和漏阻抗。

图3 配电线路单相等效电路Fig.3 Single-phase equivalent circuit of distribution lines

线路发生短路前

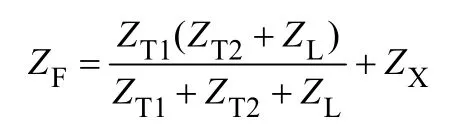
线路发生短路后

由于短路故障发生前后均有ZF>>ZS，使得380V侧短路引起的10kV侧电压U下降很小，不会形成显著电压跌落。将实际系统数据代入后计算可得380V侧发生金属性接地前后U分别为9.62kV和9.60kV，与理论分析一致。

通过上述分析可知，由于系统阻抗很小，使得380V线路侧发生的电压跌落难以有效传递到10kV线路侧。因此，当某条馈线 380V侧检测到电压跌落而 10kV侧未检测到电压跌落时，即可判定跌落源位于该馈线380V侧。

（2）10kV侧电压跌落传递能力分析

鉴于国内配电系统中性点运行方式以及配电变压器的绕组联结方式，10kV侧单相接地故障引起的电压跌落无法传递到380V侧，而10kV侧相间短路及电动机起动造成的电压跌落会通过线电压传递到380V侧。由前文分析可知，380V侧电压跌落无法有效传递到10kV侧。因此，当检测到10kV侧发生电压跌落时，即可确定电压跌落源位于 10kV或其上游侧。

1.2.3基于增益阻抗理论的改进配电网电压跌落源定位方法实施

鉴于实际系统增益阻抗虚部往往比实部更显著而易于测量，本文借助增益阻抗的虚部来对电压跌落源进行定位。方案实施过程中所需增益阻抗虚部计算过程如下。

（1）针对测量到的电压跌落发生前后每周波电压、电流数据先后进行傅里叶及对称分量分解。

（2）基于上述分解结果计算所需的各序分量及谐波下的增益阻抗。

设系统发生电压跌落前测量点处经傅里叶及对称分量分解后的电压、电流为

系统发生电压跌落后第i个周波测量点处经傅里叶及对称分量分解后的电压、电流为

根据式（1），利用电压跌落后第i个周波采集的电压、电流数据计算到的增益阻抗的虚部为

基于计算出的增益阻抗的虚部及相应判据即可判定电压跌落源的位置。由于利用电压跌落发生后每个周波数据都可计算出增益阻抗，因此可借助最小二乘法等方法对式（10）的结果进行优化以提高准确度。

本文提出的配网电压跌落源定位流程如图4所示。

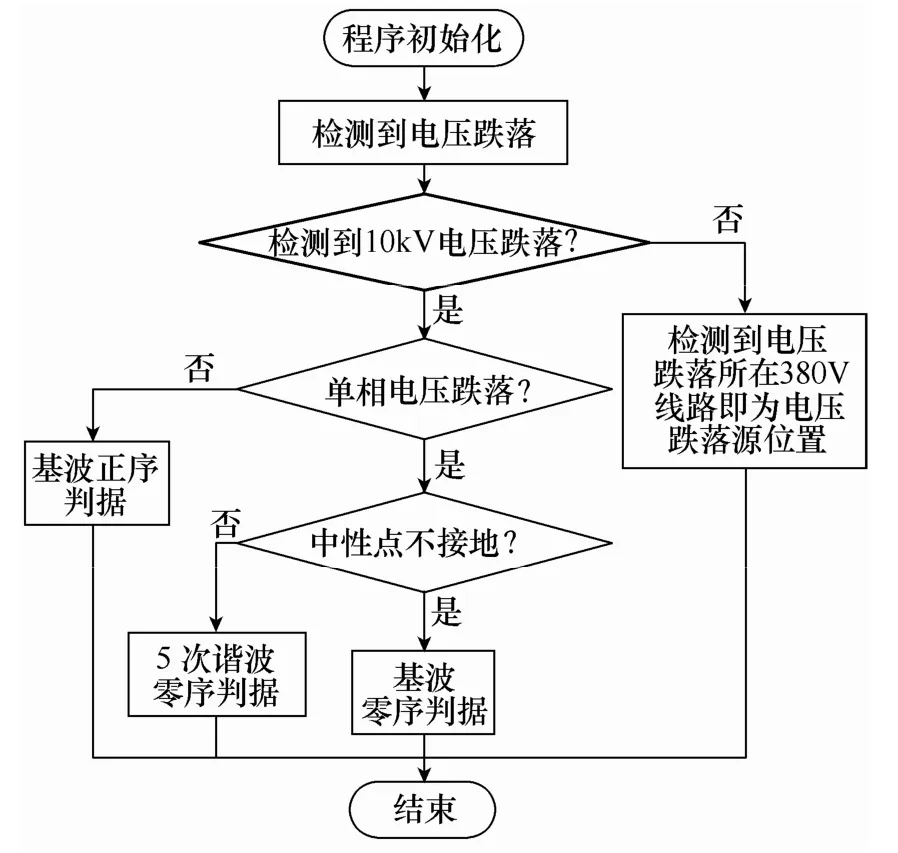
图4 基于增益阻抗理论的改进配电网电压跌落源定位流程图Fig.4 Flowchart of the modified incremental impedance based method for distribution network voltage-sag-source detection

1.2.4非线性负荷分析

在实际系统中，用户端通常存在非线性负载。而增益阻抗理论是基于线性系统通过叠加原理得出，因此有必要对本文提出的电压跌落源定位方法在非线性负荷下的有效性进行分析。非线性负荷情况下，测量点上游发生电压跌落时测量到的增益阻抗可表示为[13]

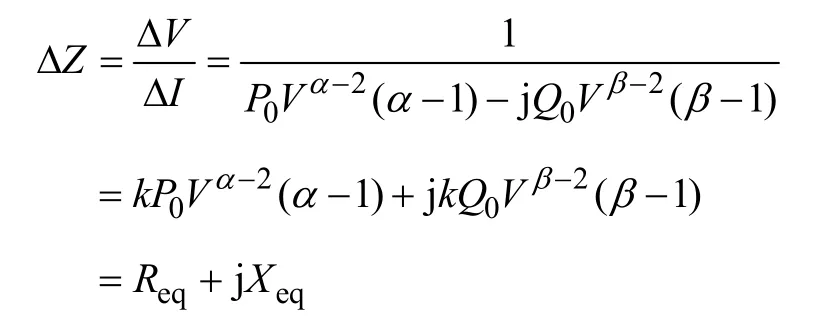
其中

式中，P0、Q0为当母线电压幅值为V时的负荷有功和无功分量。对于变频装置，α的取值范围是4.2～6.5，β的取值范围是10.6～17.9；对于感应电动机，α的取值范围是 11.0～16.1，β的取值范围是3.5～4.5。

由于k＞0，β −1＞0，因此Xeq的符号同Q0的符号一致。即当负荷为感性、吸收无功时，Q0＞0，Xeq＞0；当负荷为容性、发出无功时，Q0＜0，Xeq＜0。

由上述分析可以看出，在考虑负荷非线性情况下，通过ΔV/ΔI计算出来的增益阻抗Ze虚部的符号同实际负荷虚部的符号一致。因此，在考虑负荷非线性情况下，本文提出的电压跌落源定位判据同样有效。

1.2.5三相不平衡分析

鉴于现实中的中低压配电网不平衡度较高，因此有必要就三相不平衡现象对本文所述电压跌落源定位方法的有效性进行分析。

由前文1.2.2（1）可知，当380V侧检测到电压跌落而10kV侧未检测到电压跌落时，由于380V侧发生的各种电压跌落无法有效传递到 10kV侧，因此不需要计算增益阻抗即可判定跌落源位于 380V侧。

当跌落源位于 10kV侧中性点非有效接地系统时，本文对非对称性电压跌落采用零序增益阻抗判据进行定位，与负载无关；对于对称性电压跌落采用正序增益阻抗判据进行定位，负荷三相不平衡产生的负序电流也不会对正序增益阻抗判据造成影响。

综上所述，对于存在一定三相不平衡度的实际中低压配电系统，本文提出的电压跌落源定位判据仍然适用。

2 仿真分析

论文利用 Matlab对所提出的电压跌落源定位方法进行验证分析。仿真电路如图2所示，3条馈线，每条馈线有功负载 2MW，功率因数为0.85，其中负载构成：异步电机负载60%，阻感负载30%，非线性负载10%。谐波含量为1.11%。采样速度256点/周波，采样数据中加入随机性干扰，电压跌落前后各记录10个周波。

2.1 电压跌落源位于10kV侧的仿真分析

2.1.1中性点不接地系统

（1）单相接地短路。某条10kV线路发生单相接地故障后馈线出口处得到的增益阻抗仿真图如图5所示。

图5 中性点不接地系统10kV单相接地短路仿真图Fig.5 Simulation diagram of 10kV single-phase short of non-ground neutral system

由图5a可见，当10kV侧发生单相接地时，造成10kV侧非对称电压跌落。由图5b可以看出，电压跌落源（VSS）所在线路基波零序增益阻抗为上游系统零序增益阻抗的负值，呈感性；非电压跌落源所在线路基波零序增益阻抗为该线路下游零序增益阻抗，呈容性，与理论分析结果一致。

（2）10kV电动机起动。10kV大型电动机起动引起电压跌落仿真如图6所示。从图6a可看到电动机起动时造成明显的三相对称性电压跌落，此时应采用正序增益阻抗判据进行分析，所得基波正序增益阻抗如图6b所示，与理论分析一致，非线性负荷对本文提出的电压跌落源定位方法同样适用。

2.1.2中性点谐振接地系统

中性点谐振接地系统单相接地故障时5次谐波和基波零序增益阻抗分别如图7a和图7b所示。由图中可以看出，基波零序增益阻抗无法应用于中性点谐振接地系统的电压跌落源定位，而5次谐波零序判据可有效定位电压跌落源。

图6 中性点不接地系统10kV电动机起动仿真图Fig.6 Simulation diagram of 10kV motor starting of non-ground neutral system

图7 中性点谐振接地系统单相接地短路仿真图Fig.7 Simulation diagram of 10kV single-phase short of neutral arc-suppression-coil grounded system

2.2 电压跌落源位于380V侧的仿真分析

380V侧发生单相接地短路以及大型电动机起动时配电变压器两端电压波形分别如图8和图9所示，0.1s发生电压跌落。从图中可以看出，380V侧电压跌落难以通过配电变压器有效穿越到10kV侧。

图8 380V侧单相接地故障下的线路对地电压Fig.8 Phase to ground voltage of 380V single phase grounded fault

图9 380V大型电动机起动时线路对地电压Fig.9 Phase to ground voltage of the line large 380V motor starting

2.3 电压跌落暂态对增益阻抗计算结果的影响

仿真过程中发现，发生电压跌落后利用基波算得的增益阻抗都能够落入阻抗图的合理区域；而在某些极端情况下的电压跌落发生初期利用5次谐波算得的增益阻抗有可能无法落入合理的阻抗图区域。图10为中性点谐振接地系统三相及单相电压跌落发生前后系统基波和5次谐波零序分量幅值图。图11为图10b对应的电压跌落发生后每周波计算得到的5次谐波零序增益阻抗虚部示意图。

图10 电压跌落暂态对基波和5次谐波的影响Fig.10 Influences of voltage drop transient process on the fundamental and the fifth harmonic wave

图11 谐振接地系统高阻接地5次谐波零序增益阻抗虚部Fig.11 Imaginary part of the fifth harmonic zero sequence incremental impedance when neutral arc-suppression-coil grounded system high resistance grounding

由图10可以看出，电压跌落引起的系统基波分量的暂态过程非常平缓，而5次谐波分量暂态过程却异常剧烈，通过综合分析图10和图11可知：

（1）基波增益阻抗的计算过程有效滤除了暂态过程中非周期分量对系统中含量丰富的基频成分的影响，因此电压跌落发生后任一周波计算得到的基波增益阻抗都可有效反映系统的实际阻抗。

（2）5次谐波增益阻抗的计算过程无法有效滤除暂态过程中的非周期分量对系统中含量较低的5次谐波成分的影响，因此利用电压跌落发生初期计算出的5次谐波增益阻抗可能无法准确反映系统的实际5次谐波阻抗。

由于图11是在高阻接地这一系统5次谐波极易受到暂态过程干扰的极端情况下得到的，因此结合大量仿真结果，为了提高5次谐波增益阻抗判据的有效性，应尽量采用电压跌落发生3个周波之后的数据计算5次谐波增益阻抗。而鉴于系统中实际发生的绝大多数电压跌落的持续时间为4～10个周波[17,18]，因此5次谐波零序增益阻抗应用于中性点谐振接地系统的单相电压跌落源定位是可行的。

3 模拟实验

模拟实验电路如图12所示，除电压等级外，其他参数按照10kV等级设置，具体参数见下表。

线路1发生单相及三相短路时得到的模拟实验结果分别如图13和图14所示。

需要注意的是，在模拟实验中线路阻抗不能忽略，因此图14b非VSS所在线路的基波正序增益阻抗明显大于负载等效阻抗。

可见模拟实验结果与理论、仿真分析结果一致。

图12 模拟实验电路图Fig.12 Circuit of simulation experiment

表 模拟试验参数Tab.Simulation experiment parameters

图13 单相电压跌落模拟实验结果Fig.13 Results of single-phase voltage sag simulation experiment

图14 三相电压跌落模拟实验结果Fig.14 Results of three-phase voltage sag simulation experiment

4 结论

本文在原有基于增益阻抗实部的电压跌落源定位方法基础上，将电压跌落源的初步辨识引入其中，提出了一种基于电压跌落源类型的改进型定位方法，并将其应用于国内配电系统，发展出一套国内辐射型配电系统电压跌落源定位方案，理论、仿真分析及模拟实验都验证了该方法的有效性。

该方法物理概念明确，现场可实施性强，对含有线性和非线性负荷的系统均适用，但其应用于环形供电、双向供电等结构复杂的配电网络时的有效性还有待于进一步研究。

[1] IEEE Std.1159—1995.Recommended practice for monitoring electric power quality[S].1995.

[2] 李庚银,杨晓东,周明.复杂配电网的电压暂降随机预估方法[J].电工技术学报,2009,24(11):134-141.

Li Gengyin,Yang Xiaodong,Zhou Ming.Stochastic estimation method of voltage sags in complex distribution systems[J].Transactions of China Electrotechnical Society,2009,24(11):134-141.

[3] 林焱,吴丹岳,章雪萌,等.电压暂降指标的探讨[J].电力系统保护与控制,2010,38(3):147-152.

Lin Yan,Wu Danyue,Zhang Xuemeng,et al.An exploration on index about voltage sags[J].Power System Protection and Control,2010,38(3):147-152.

[4] 雷刚,顾伟,袁晓冬.考虑系统与敏感负荷兼容性的电压暂降指标[J].电工技术学报,2010,25(12):132-138.

Lei Gang,Gu Wei,Yuan Xiaodong.A voltage sag index considering compatibility between system and sensitive equipment[J].Transactions of China Electrotechnical Society,2010,25(12):132-138

[5] 陶顺,肖湘宁,刘晓娟.电压暂降对配电系统可靠性影响及其评估指标的研究[J].中国电机工程学报,2005,25(21):66-72.

Tao Shun,Xiao Xiangning,Liu Xiaojuan.Study on distribution reliability considering voltage sags and acceptable indices[J].Proceedings of the CSEE,2005,25(21):66-72.

[6] 吕干云,孙维蒙,汪晓东,等.电力系统电压暂降源定位方法综述[J].电力系统保护与控制,2010,38(23):241-245.

Lv Ganyun,Sun Weimeng,Wang Xiaodong,et al.Review on methods for voltage sag source location in power system[J].Power System Protection and Control,2010,38(23):241-245.

[7] Parsons A C,Grady W M,Powers E J,et a1.A direction finder for power quality disturbances based upon disturbance power and energy[J].IEEE Transactions on Power Delivery,2000,15(3):1081-1086.

[8] 张文涛,王成山.基于改进扰动功率和能量法的暂态扰动定位[J].电力系统自动化,2007,31(8):31-34.

Zhang Wentao,Wang Chengshan.Transient disturbances location based on improved disturbance power and energy[J].Power System Technology,2007,31(8):31-34.

[9] Kong Wei,Dong Xinzhou,Chen Zhe.Voltage sag sourcelocation based on instantaneous energy detection[J].Electric Power Systems Research,2008,78(3):1889-1898.

[10] Li C,Tayjasanant T,Xu W.Method for voltage sag source detection by investigating slope of the system trajectory[J].IEEE Proceedings:Generation,Transmission and Distribution,2003,150(3)：367-372.

[11] Pradhan A K,Routray A.Applying distance relay forvoltage sag source detection[J].IEEE Transactions on Power Delivery,2005,20(3):529-531.

[12] 吕干云,孙维蒙,汪晓东,等.利用三点法的电压暂降源定位方法[J].中国电机工程学报,2011,31(7):36-40.

Lü Ganyun,Sun Weimeng,Wang Xiaodong,et al.Voltage sag source location based on three-point method[J].Proceedings of the CSEE,2011,31(7):36-40.

[13] Tayjasanant Thavatchai,Li Chun,Xu Wilsun.Resistance sign-based method for voltage sag source detection[J].IEEE Transactions on Power Delivery,2005,20(4):25-44.

[14] 朱珂,徐文远.基于等效阻抗理论的故障选线方法[J].电力自动化设备,2007,27(11):18-21.

Zhu Ke,Xu Wenyuan.Faulty line detection based on incremental impedance theory[J].Electric Power Automation Equipment,2007,27(11):18-21.

[15] 楼书氢.配电网中电压暂降源的识别与定位[D].北京:华北电力大学,2007.

[16] 陶顺,肖湘宁.中性点不同接地方式下的电压暂降类型及其在变压器间的传递（二）[J].电工技术学报,2007,22(10):156-159.

Tao Shun,Xiao Xiangning.Voltage sags types under different grounding modes of neutral and their propagation:partⅡ[J].Transactions of China Electrotechnical Society,2007,22(10):156-159.

[17] Gunther E W,Metha H.A study of distribution system power quality—preliminary results[J].IEEE Transactions on Power Delivery,1995,10(1):322-329.

[18] Tang L,Lamoree J,Mcgranaghan,et al.Distribution system voltage sags:interaction with motor and drive loads[C].Proceedings of IEEE Transmission and Distribution Conference,Chicago,USA,1994:1-6.