基于散射中心模型的典型目标宽带雷达回波仿真
2015-11-15潘明海
蔡 武,潘明海
(南京航空航天大学 雷达成像与微波光子技术教育部重点实验室,南京 210016)
0 引 言
雷达目标回波模拟是雷达仿真的关键部分,宽带雷达目标回波信号有别于点目标回波信号,不再是简单的发射信号的延迟、多普勒频移以及幅度调制,而应看作是雷达的发射信号经过一个系统后的输出信号,该系统函数取决于目标的信息,反映了目标的电磁散射特性。因此,宽带雷达目标信号模拟是通过将雷达发射信号与目标散射特性数据进行卷积运算后,再经过时延控制和多普勒频率调制得到的,能够准确复现目标的电磁散射特性及其距离、速度等信息[1-2]。
1 宽带目标散射特性
雷达目标散射特性是回波仿真中的一个重要环节。在高频区,由局部性定理可知,目标总的电磁散射可以认为是由某些局部位置上的电磁散射合成的,这些局部性的散射源通常被称为散射中心[1],即目标散射不是全部目标表面所贡献的,而是用多个孤立散射中心来完全表征的。
目标散射中心的主要类型可以分为镜面散射、边缘(棱线)散射、尖顶散射、腔体散射、行波和蠕动波散射以及天线型散射等。
在目标散射特性研究中,一般采用反射率函数ζ(t)作为目标不同部位的电磁散射特性的时域表征[3],与目标的冲击响应等价,根据文献[4],ζ(t)表示为

式中:δ(n)(·)取正值表示冲击函数δ(·)的n 次微分,取负值则表示积分,取0 值表示冲击函数本身。将式(2)变换到频域得到

式中:Hm(f)为雷达视线方向上该散射中心的频域特性;m 表示扩展目标的第m个散射中心;FT 为傅里叶变换算子;Am是第m个散射中心的散射强度;f 代表雷达发射信号频率,起始频率为f0。
宽带雷达通常工作在高频区,可以采用基于几何绕射理论的散射中心GTD 模型[5-6]来描述目标高频电磁散射特性,并将n 用α 代换,式(3)可近似为

式中:αm表征第m个散射中心的类型;rm表示第m个散射中心与目标相位零点的相对距离。
目标在高频区的时域目标特性通过公式(4)进行逆傅里叶变换得到

通过对实测数据或电磁计算数据进行分析,从中提取散射中心参数。在一定的姿态角下,利用电磁软件根据目标的3DS 模型计算得到目标散射特性数据。采用基于全局最小二乘-旋转不变技术(TLS_ESPRIT)的方法来提取目标的一维散射中心[8-10]。将得到的r,A,α,带入公式(5),得到散射中心时域散射特性。
采用上述方法提取到的F-22 战斗机在雷达径向方向上的10个较强散射中心参数如表1 所示,散射中心的相对位置分布图如图1 所示。

表1 F-22 战斗机散射中心参数

图1 散射中心位置分布图
对计算得到的单个散射中心的目标特性进行分析,取目标的第一个散射中心,即α1= 1.0,A1=0.001 8,r1= 2.68 m 时,代入式(4),得到该散射中心频域的目标特性。
将频域特性进行逆傅里叶变换,得到散射中心1 的时域散射特性如图2 所示。从图2 中可以看出,该散射中心频域特性转化为时域特性以后,除了峰值周围的数据以外,其余大部分数据接近于零,为了简化卷积运算量,取峰值为中心32点数据作为该散射中心时域特性,其余点数全部取零舍去。

图2 散射中心1 的时域特性
2 基于散射中心回波模型
目标包含多个强散射中心时,其回波信号就是各个散射中心的回波信号的矢量和,雷达发射信号为线性调频信号时散射中心模型目标回波为
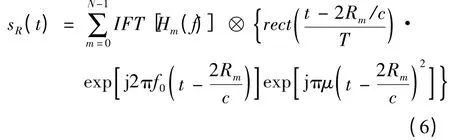
式中:IFT[·]为傅立叶逆变换运算算子;⊗为卷积运算;Rm= r0+ rm,Rm为散射中心m 与雷达之间的径向距离,r0为目标相位零点与雷达之间的径向距离;调频斜率μ = 2πB/T,B 为发射信号带宽,T 为发射脉冲宽度;发射信号的波长λ = c/f,对于线性调频信号有

回波仿真之后,可以运用匹配滤波法进行脉冲压缩得到目标的一维距离像[11],检验回波仿真的效果,验证散射中心在径向上的分布。匹配滤波器与发射信号具有相同的调频斜率,但方向相反,表达式为

实现脉冲压缩可以在时域进行,也可以在频域进行。它们的本质是相同的,但是在频域进行可以借助快速傅里叶变换减少运算量。对基带回波信号去载频后采样,得到匹配滤波器的输入信号S(k);对匹配滤波器S1(t)采样得到S1(k),基带回波信号S(k)和匹配信号S1(k)通过图3 所示的脉冲压缩过程得到一维距离像,即散射中心的径向分布。
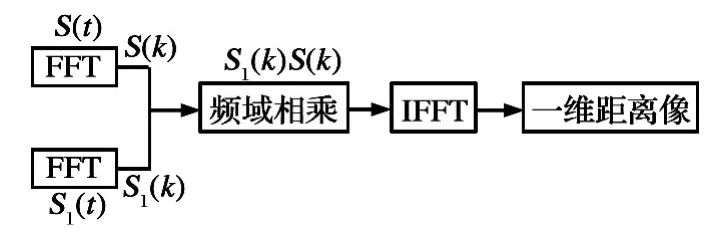
图3 脉冲压缩原理图
3 仿真实验及分析
3.1 目标回波仿真及分析
首先由目标的散射特性提取出目标的散射中心参数,由散射中心回波模型得到目标的基带回波,最后脉冲压缩产生一维距离像。具体目标散射中心模型回波仿真原理图如图4 所示。

图4 目标回波仿真原理图
宽带雷达发射信号采用线性调频信号,中心频率为9.25 GHz,脉冲宽度T = 5 μs,线性调频信号带宽为B = 500 MHz,采样率为1.2 GHz。
目标为表1 所示的F-22 战斗机散射中心模型,目标与雷达之间的距离为40 km,目标相对于雷达方位为0°、俯仰角为0°,目标共有10个一维的散射中心,采用所提出的方法对回波进行仿真,目标回波时域波形如图5 所示。

图5 F-22 的时域回波信号
从图5 中可以看出,回波是对发射信号进行复杂调制的结果,幅度和相位都发生了变化,而且目标回波脉冲相对于发射脉冲宽度T 有一定展宽,每个散射中心对应的发射信号与散射中心时域序列通过卷积运算之后,回波脉冲宽度变为T + (n-1)Ts= T +31Ts,Ts为采样频率1.2 GHz 时信号的取样间隔。发射信号采样点为6 000 点,雷达目标回波脉冲为6 121个点,脉冲展宽了121个采样间隔,约100.5 ns。
目标所有的散射中心的时域回波脉冲,经过时延处理并相加后获得的目标距离向回波脉冲宽度变为T+31Ts+2L/c,L 为目标的距离向长度,即散射中心1 与散射中心10 之间的距离为L =10.89 m,代入该公式计算得到雷达目标回波脉冲的展宽为100.5 ns,与仿真结果相同。
图6 是目标回波信号的频谱的仿真结果。由图6 可知,宽带目标的雷达回波的频谱特征与雷达发射信号的频谱密切相关,频谱幅度呈现复杂的调制特征。由于各个散射中心的强弱,距离分布不同,其受频率变化影响也不相同。
3.2 一维距离像

图6 基带回波信号频谱
对回波进行匹配滤波以后得到图7 所示的目标的一维距离像。图7 中的一维像的距离向宽度为20 m,与提取的散射中心宽度相比,发生了展宽;而且散射点的数目与表1 的数目也不吻合,得到距离向上仅有9个明显的散射中心,这是由于雷达的带宽为500 MHz,此时雷达的距离分辨率为c/2B,此例中为0.3 m,其中散射中心6 和7 之间距离为0.26 m,小于分辨单元,因此,脉冲压缩后散射中心脉冲产生重合,无法分辨。
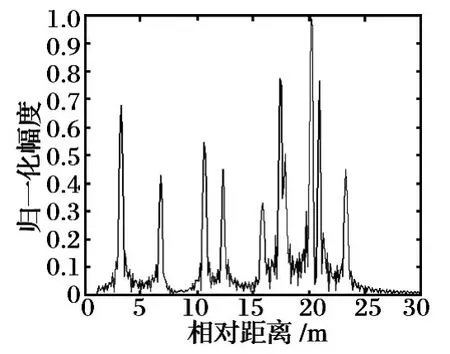
图7 F-22 匹配滤波后的回波
将图7 与图1 进行比较,发现脉压后得到的一维距离像发生偏移。这是由于计算时取散射中心的时域散射序列长度为32个(采样频率为1.2 GHz),但是每个散射中心对应的时域目标特性各不相同,峰值在序列中的位置并不相同,并且由于卷积运算回波脉冲发生了展宽,造成了一维距离像在距离上的偏移。
对前两个散射中心分析,散射中心1 与散射中心2 相对距离为1.99 m,采样率为1.2 GHz 时,正确的一维距离像间距为16个采样间隔,图7 中的相对距离偏移约为3.5 m,间隔变为28个,产生了不小的偏差,对于散射中心位置判断来说影响很大。产生偏移是因为散射中心1 与散射中心2 距离、类型等的不同,造成时域散射特性也不尽相同。
图8 为散射中心2 的时域特性曲线,与图2 相比,峰值的时间并不相同,卷积计算时以峰值为中心取32 点进行卷积计算,因此,散射中心1 回波与散射中心2 回波相加时,除了要考虑时延,还要考虑不同散射特性对其回波的影响。对于散射中心1和2,其回波的距离时延相差16个采样间隔,时域特性曲线峰值时间相差10 ns,即12个采样间隔,两者相加,为28个采样间隔,与图8 所示的仿真结果相同,说明匹配滤波以后得到的距离像之间的差值,减去时域特性峰值之间的差值以后,得到的就是正确的一维距离像,如图9 所示。

图8 散射中心2 的时域特性曲线

图9 F-22 精确一维距离像
将图9 得到的散射中心分布与图1 进行比较,可以看出,经过处理之后的一维距离像与正确的散射中心分布在幅度、距离上都很符合,证明了方法的有效性。
将仿真得到的散射中心位置、幅度与提取到的原始数据进行误差分析,得到表2 所示的各散射中心位置、幅度误差。由表2 可以看出,仿真得到的位置精度很高,误差均小于2%,证明了仿真的正确性;幅度误差相对于位置误差很大,但是均小于5%,由于散射中心6,7 的一维距离像脉冲产生重合,所以散射中心6 的幅度产生了较大的偏差。
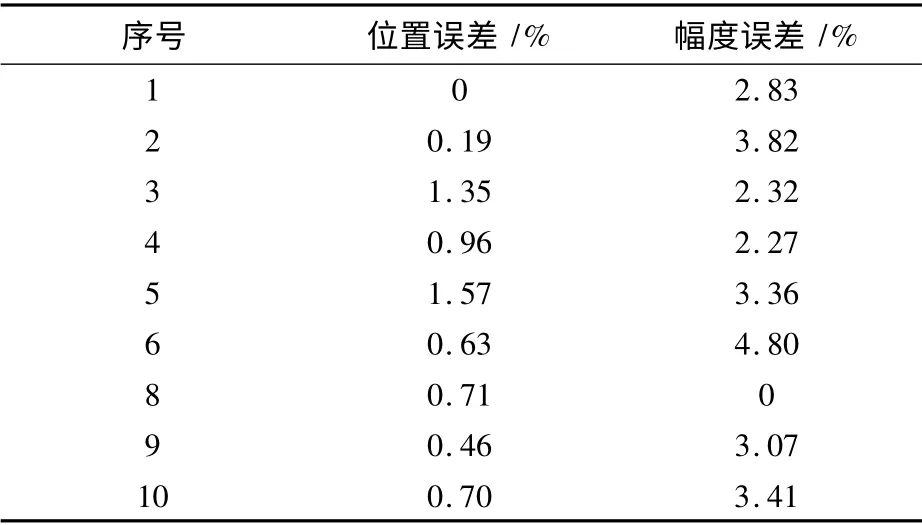
表2 散射中心位置、幅度误差
4 结 束 语
本文提出了流程清晰、完整的宽带目标回波仿真方法,结合提取出的目标散射中心参数,得到典型目标的回波仿真,并且利用脉冲压缩得到一维距离像。对得到的一维距离像进行分析与校对,得到精确的一维距离像,并对仿真得到的散射中心位置、幅度进行了误差分析,进一步证明了仿真方法的正确性。
[1]梁志恒,潘明海.毫米波导引头目标回波和杂波模拟方法研究[J]. 系统仿真学报,2007,19(12):2723 -2726.
[2]王海彬.基于高频电磁散射理论的电大复杂目标宽带雷达回波快速计算方法[J]. 电子学报,2010,38(3):561 -566.
[3]黄培康,殷成红,徐小剑.雷达目标特性[M].北京:电子工业出版社,2005:247 -254.
[4]程肖. 基于散射中心模型的SAR 图像自动目标识别[D].长沙:国防科学技术大学,2009:15 -28.
[5]于宵晖,罗鹏飞.线性调频脉冲压缩雷达视频回波模型[J].雷达科学与技术,2010,8(2):101 -103.
[6]Poter L C,Chiang D M. A GTD-Based Parametric Model for Radar Scattering[J]. IEEE Transaction on Antennas and Propagation,1995,43(10):1058 -1066.
[7]Bhalla R,Moore J,Ling H. A Global Scattering Center Representation of Complex Targets Using the Shooting and Bouncing Ray Technique[J].IEEE Transaction on Antennas Propagation,1997,45(12):1850 -1856.
[8]贺治华,张旭峰. 一种GTD 模型参数估计的新方法[J].电子学报,2005,33(9):1679 -1682.
[9]Roy R,Kailath T. ESPRIT -Estimation of Signal Parameters via Rotational Invarance Techniques[J]. IEEE Transaction on ASSP,1989,37:984 -995.
[10]王菁. 光学区雷达目标散射中心提取及其应用研究[D].南京:南京航空航天大学,2010.
[11]保铮,邢孟道,王彤. 雷达成像技术[M]. 北京:电子工业出版社,2006:24 -30.
[12]张安. 高分辨海面目标动态回波模拟实现技术研究[D].长沙:国防科技大学,2011.
