基于单胞体模型的复合固体推进剂松弛模量衰减过程数值模拟

何 涛

(海军航空装备计量监修中心，上海200436)

0 引 言

随着世界军事科技的发展，导弹性能的不断提高，对固体火箭发动机性能的要求越来越高。如何在保证固体火箭发动机装药结构完整性的前提下，尽可能地提高发动机的装药量，一直是固体火箭发动机设计过程中需要解决的关键问题。要解决该问题，首先必须要展开固体推进剂力学性能的研究。复合固体推进剂是一种多相(基体、增强相、界面相等)复合材料，其力学性能受增强相的体积分数及其组分材料性质的影响比较大。因此，基于细观力学理论研究复合固体推进剂非线性力学性能，不仅可以直观地反映出组分材料的影响，还可以对其宏观非线性本构关系的研究提供理论支撑。

复合固体推进剂是一种高填充比的复合材料。近些年来，随着计算机性能的大幅度提高，计算细观力学得到了迅速发展。Matous 等［1-2］在复合固体推进剂颗粒与基体之间的界面层设置了粘结单元(Cohesive element)模拟了固体颗粒和基体之间损伤的产生及发展。Tan 等［3-4］通过数字图象等相关技术获得了高能炸药PBX9501 紧凑拉伸试样裂尖周围的应力场及位移场，利用扩展的Mori-Tanaka 方法对试验结果做了均匀化处理，并结合试验研究得到的颗粒与基体之间的非线性粘结模型，对含不同尺寸颗粒的细观模型进行了数值计算。国内一些学者研究了复合固体推进剂的颗粒夹杂模型的建模方法［5-7］。在此基础上，有的学者采用有限元法对复合固体推进剂进行直接数值模拟，对推进剂内部界面脱粘过程进行了有限元分析［8］。有的学者根据数值仿真结果，结合细观力学方法，如:Mori-Tanaka 方法或改进的Mori-Tanaka 方法，研究了固体推进剂的模量、界面脱粘对固体推进剂力学性能的影响等［9-11］，或采用多步法，通过将基体与部分颗粒均质化为一种混合物，计算出较复杂的固体推进剂的有效模量［12］。

本文在之前研究［13-14］的基础上，通过建立复合固体推进剂单胞体模型，根据复合固体推进剂松弛模量试验值对基体材料的松弛模量进行参数反演，结合数值计算方法对复合固体推进剂松弛模量的衰减特性进行了研究。

1 物理模型和计算方法

1.1 颗粒夹杂模型及组分材料属性

复合固体推进剂是一种典型的颗粒增强复合材料，由于颗粒粒径的分布特征及颗粒的随机分布，使得其微结构特征非常复杂，如图1 所示。

图1 复合固体推进剂颗粒堆积模型及网格

从图1 中可以看出，复合固体推进剂颗粒堆积模型可以更真实地反映其微结构特征，但这种模型建模过程复杂，并且由于颗粒之间距离较近，使得网格密度较大，计算量较大，这在后续工作中将逐步展开研究。本文旨在研究复合固体推进剂松弛模量应变的衰减特性，因此首先从单胞体模型出发进行研究。根据复合固体推进剂的固体含量确定AP 颗粒的体积分数，本文所研究的复合固体推进剂AP 颗粒体积分数为65%，单胞体模型如图2 所示。

图2 复合固体推进剂单胞体模型

由之前研究［13］可知，复合固体推进剂的松弛特性主要来源于基体材料，在AP 颗粒的增强作用下，复合固体推进剂的松弛特性与基体材料基本一致，区别主要体现在瞬时模量E0的增大。因此，基于图2 所示模型，根据复合固体推进剂的松弛模量对基体材料的松弛模量进行参数反演。首先确定基体瞬时模量E0的上、下限值和，并根据已确定的上、下限值进行有限元计算，结合细观力学方法，得出基体瞬时模量E0的上、下限值所对应的复合固体推进剂瞬时模量和;然后对比复合固体推进剂的实际瞬时模量EP0，根据EP0在和之间的线性分布关系，在和之间确定下一步计算时新的基体瞬时模量取和的平均值为新的，再次进行有限元计算;反复进行迭代，最后确定基体的松弛模量。假设AP 颗粒为弹性体，取其弹性模量和泊松比分别为:E=32 450 MPa，ν=0.143 3［1］。

1.2 均匀化方法

当复合固体推进剂单胞体模型受载荷作用时，其体积平均应力和平均应变可由式(1)～(2)计算:

当AP 颗粒体积分数为65%时，图2 模型中颗粒之间距离很小，基体材料部分若采用六面体网格，在颗粒之间临近部分，网格易产生畸变。因此，对于AP 颗粒可采用六面体网格，基体材料部分采用四面体网格。根据有限元高斯积分原理，分别计算单个六面体单元和四面体单元的平均应力、应变。模型的体积平均应力和应变可以通过单个六面体网格和四面体网格的平均应力和平均应变来确定，即

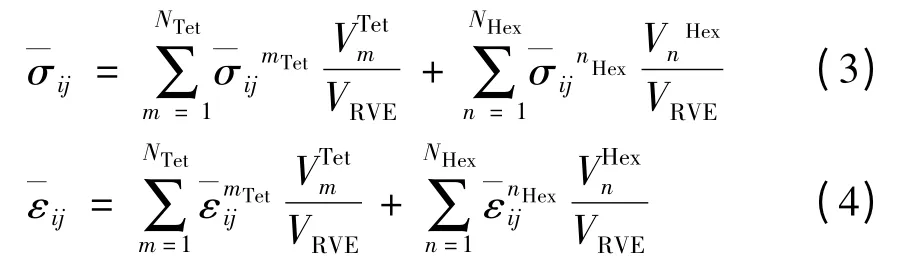
2 计算结果及讨论

复合固体推进剂松弛模量一般是根据GJB -770B 在定应变5%下测量的。根据复合固体推进剂定应变为5%时的松弛模量，结合均匀化方法对基体材料的松弛模量进行参数反演，获得基体材料的松弛模量。定应变为5%时单胞体模型拉伸方向上的应力分布如图3 所示。从图中可以看出，应力较大的区域主要集中在颗粒间距小的区域，随着时间的增大，应力有明显的松弛效应。

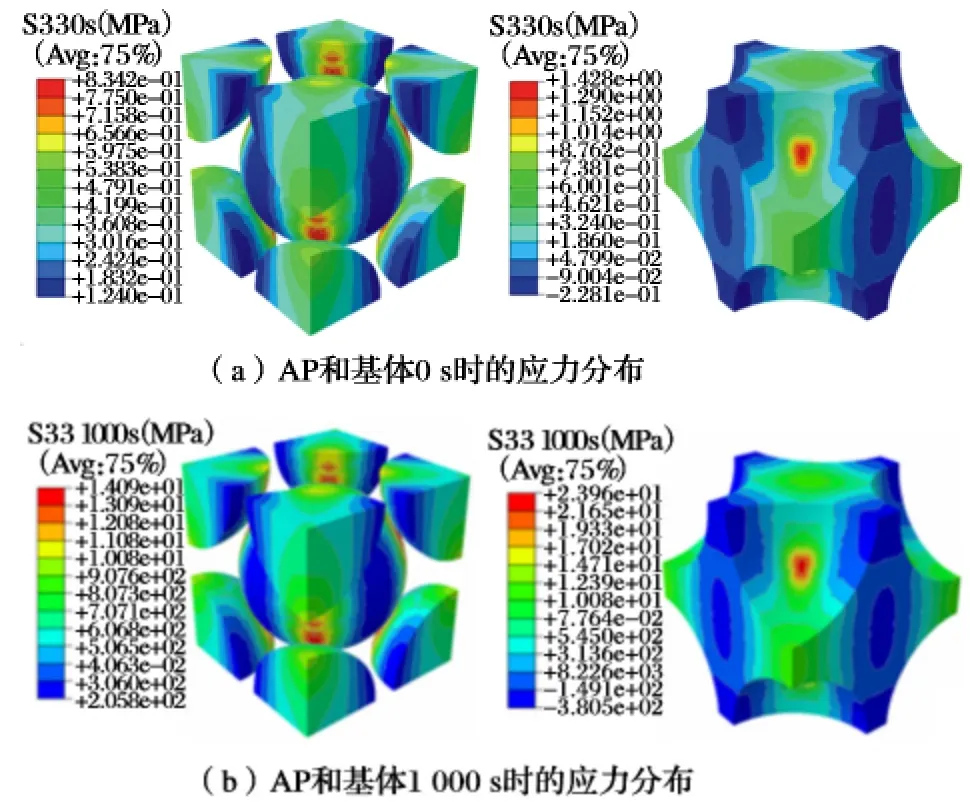
图3 定应变为5%时单胞体模型的应力分布

为研究复合固体推进剂松弛模量的应变相关性，假设基体的松弛模量不变，应变小于8%时忽略界面损伤的影响，分别计算当定应变为0.01%，1%，2%，3%，4%，5%，6%，7%，8%时复合固体推进剂的松弛模量，如图4 所示。从图中可以明显看出，当定应变较小时所计算的松弛模量较大，随着定应变值的增大，复合固体推进剂松弛模量逐渐减小。所得结论与Özüpek［15］根据不同定应变(0.5%，1%，2%，5%，10%和15%)下测得的松弛模量试验结果得到的结论一致。

分别对单胞体模型及复合固体推进剂均质材料模型的拉伸过程进行数值计算。其中，复合固体推进剂均质材料模型采用不同定应变下的松弛模量。拉伸时间分别取0.05 s 和100 s，最终的真实应变均为7.16%。计算结果如图5 和图6 所示。从图中可以看出，采用不同定应变水平下的松弛模量的拉伸曲线与单胞体模型的拉伸曲线有明显差异，只有当真实应变约小于3%时，所选取定应变值越低松弛模量的计算结果与单胞体模型的计算结果越接近。

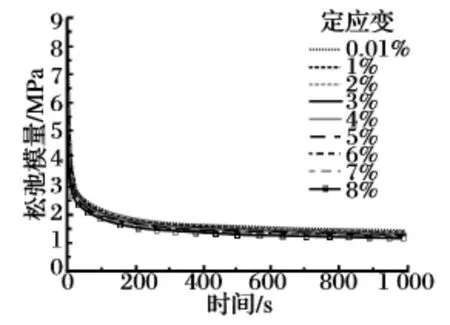
图4 不同定应变水平下的复合固体推进剂松弛模量曲线

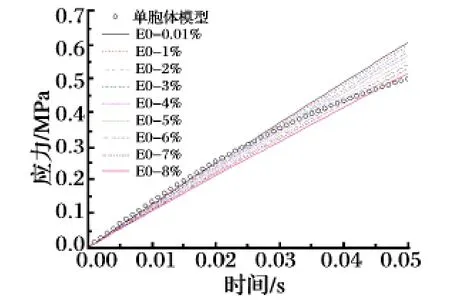
图5 0.05s 内单胞体模型及推进剂拉伸曲线

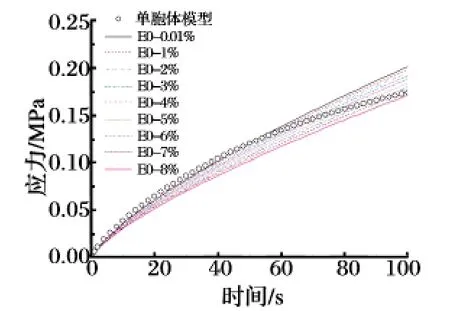
图6 100 s 内单胞体模型及推进剂拉伸曲线

根据Boltzmann 叠加原理，多个起因的总效应等于各个起因的效应之和。对于一维模型，当有n个应变增量顺次在ζi时刻分别作用于物体，则在ζn以后某时刻t 的总应力可表示为

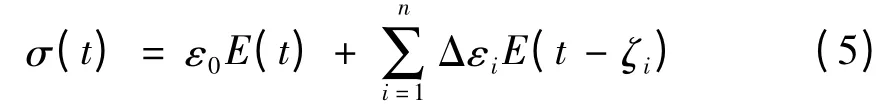
对于三维模型，当时间增量Δt 足够小时，Δσij，Δεij应满足广义胡克定律，即

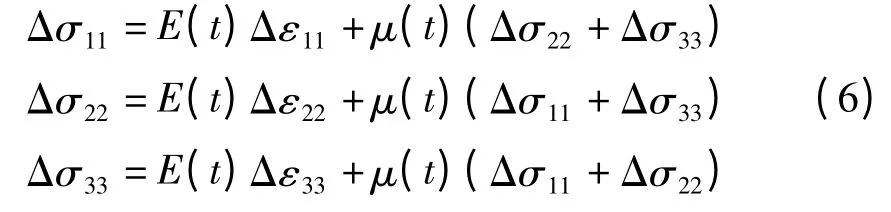
因此，可根据单胞体模型的拉伸曲线，选取一定的时间增量Δt，求解出t 时刻时的松弛模量E(t)，对比初始时刻的松弛模量曲线，从而获得瞬时模量E0的变化。为验证该方法及确定合适的时间增量Δt，以复合固体推进剂定应变为5%时的松弛模量为输入条件，拉伸时间为0.05 s，取Δt 分别为0.001 s，0.000 5 s 和0.000 1 s 计算复合固体推进剂的松弛模量，并与输入的松弛模量进行对比，相对误差如图7 所示。从图中可以看出，相对误差随时间的增大而增大，这是因为随着计算时间的增加，在t ～t+Δt 时刻内，时间t 之前累计载荷的松弛效应逐渐增大，而在计算的过程中忽略了Δt 时刻内松弛效应的影响。虽然相对误差随时间的增大而增大，但数值仍然较小，说明了该计算方法可行。从不同时间增量Δt 的计算结果来看，当Δt 从0.001 s 缩小10 倍后，相对误差产生了震荡，并且减小Δt 时相对误差降低的幅度不大。输入条件不变，拉伸时间改为100 s，Δt 取0.001 s，计算的松弛模量与理论值对比如图8 所示。当拉伸时间为100 s 时，相对误差为0.83%。采用该方法可以根据复合固体推进剂的拉伸曲线计算松弛模量的变化。

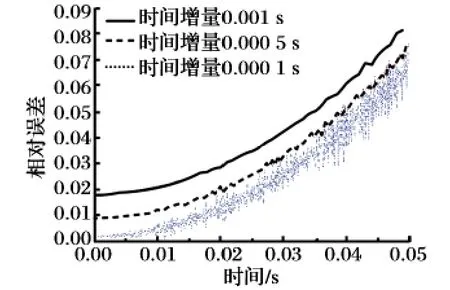
图7 拉伸时间为0.05 s 时的松弛模量相对误差

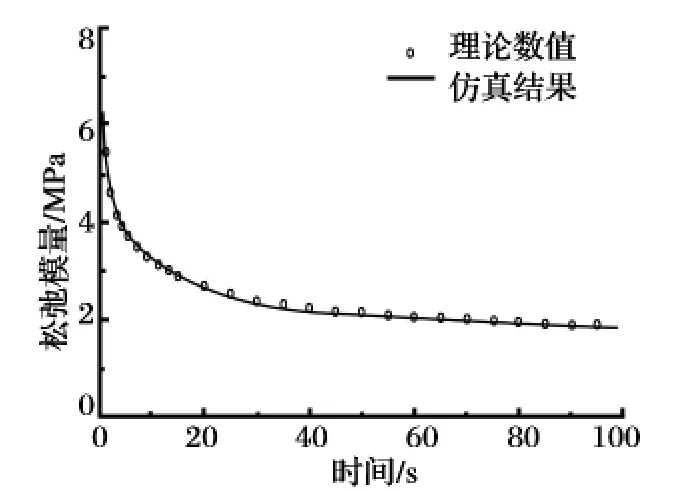
图8 拉伸时间为100 s 时的计算值与理论值对比

选取时间增量Δt 为0.001 s，最终真实应变为7.16%，拉伸时间分别取0.05 s 和100 s 时，复合固体推进剂单胞体模型松弛模量的衰减如图9 和图10 所示。从图中可以看出，在复合固体推进剂单胞体的拉伸过程中，模量有明显的衰减现象，衰减程度与载荷历程相关。

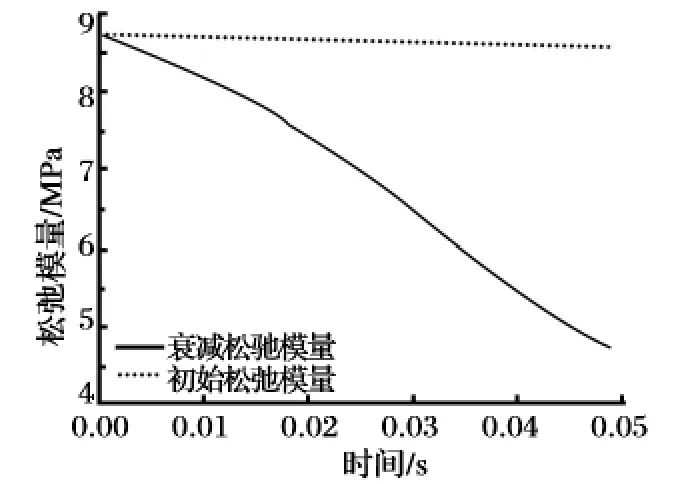
图9 拉伸时间为0.05 s 时的松弛模量衰减

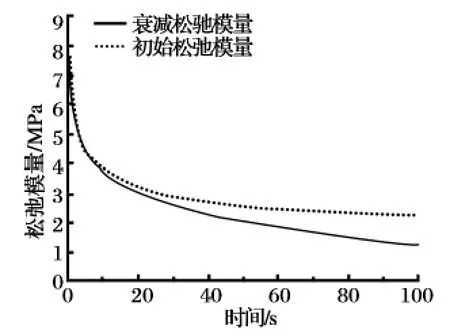
图10 拉伸时间为100 s 时的松弛模量衰减

3 总 结

(1)由于复合固体推进剂材料的颗粒夹杂效应，通过仿真计算可知其松弛模量具有明显的应变相关性，即在不同的定应变水平下测得的试验结果会存在差异，随着定应变水平的增大，测得的松弛模量逐渐减小。计算结果所得结论与Özüpek［15］试验结果一致。

(2)根据单胞体模型不同拉伸速率下，不考虑界面损伤时的拉伸曲线，计算了拉伸过程中复合固体推进剂松弛模量的变化。计算结果表明，在拉伸过程中，复合固体推进剂的松弛模量有明显的衰减现象，并且衰减程度与载荷历程相关。

［1］Matous K，Inglis H M，Gu X F，et al. Multiscale Damage Modeling of Solid Propellants:Theory and Computational Framework［C］//41st AIAA/ASME/SAE/ASEE Joint Propulsion Conference ＆ Exhibit，AIAA 2005 - 4347，2005:1 -14.

［2］Matous K，Geubelle P H. Multiscale Modeling of Particle Debonding in Reinforced Elastomers Subjected to Finite Deformation［J］. International Journal for Numerical Methods in Engineering，2006，65(2):190 -223.

［3］Tan H，Liu C，Huang Y，et al. The Cohesive Law for the Particle/Matrix Interfaces in High Explosives［J］. Journal of the Mechanics and Physics of Solids，2005，53(8):1892 -1917.

［4］Tan H，Huang Y，Liu C，et al. The Uniaxial Tension of Particulate Composite Materials with Nonlinear Interface Debonding［J］. International Journal of Solids and Structures. 2007，44(6):1809 -1822.

［5］史佩，李高春，李昊. 复合固体推进剂细观力学模型研究［J］. 计算机仿真，2007，24(5):21 -24.

［6］赵玖玲，田先斌. 颗粒复合材料代表性体元并行建模算法研究［J］. 计算机仿真，2010，27(1):46 -49.

［7］刘著卿，李高春，邢耀国. 复合固体推进剂细观损伤扫描电镜实验及数值模拟［J］. 推进技术，2011，32(3):412 -416.

［8］曲凯，张旭东，李高春. 基于内聚力界面脱粘的复合固体推进剂力学性能研究［J］. 火炸药学报，2008，31(6):77 -81.

［9］李高春，邢耀国，王玉峰. 基于细观力学的复合固体推进剂模量预估方法［J］. 推进技术，2007，28(4):441 -444.

［10］李高春，邢耀国，戢治洪，等. 复合固体推进剂细观界面脱粘有限元分析［J］. 复合材料学报，2011，28(3):229 -235.

［11］刘承武，阳建红，陈飞. 改进的Mori-Tanaka 法在复合推进剂非线界面脱粘中的应用［J］. 固体火箭技术，2011，34(1):67 -70.

［12］马昌兵，强洪夫，武文明，等. 颗粒增强复合材料有效弹性模量预测的多步法［J］. 固体力学学报，2010，31(S1):12 -16.

［13］Zhi Shijun，Sun Bing，Zhang Jianwei. Multiscale Modeling of Heterogeneous Propellants from Particle Packing to Grain Failure Using a Surface-Based Cohesive Approach［J］. Acta Mechanica Sinica，2012，28(3):746 -759.

［14］职世君，孙冰，张建伟. 基于表面粘结损伤的复合固体推进剂细观损伤数值模拟［J］. 推进技术，2013，34(2):273 -279.

［15］Sebnem Özüpek. Constitutive Equations for Solid Propellants［D］. University of Texas at Austin，1997.