基于量子粒子群算法的城市物流配送路径研究

□文/周 媛 解翠杰 高田娟

（河北交通职业技术学院 河北·石家庄）

一、引言

配送路线的合理优化属于NP（Non-deterministic Polynomial）问题，是车辆路径优化问题（VRP）中的典型问题，由Dantzig和Ramser于1959年首次提出，历经数十年的研究，已经成为运筹学与组合优化领域的研究热点课题。

二、追求共赢的配送路径系统模型

（一）客户满意度模型。传统的车辆路径问题用时间窗口作为运输服务的时间约束。结合实际，客户倾向于某一时间段内得到服务，［τ1i，τ2i］表示客户可容忍的服务时间范围，［ai，bi］为客户期望的服务时间范围，对于图中所描述的客户i其满意度函数可表示为:

（二）配送中心配送运输经济效益模型。配送中心的配送运输任务总是围绕经济效益，根据Fisher市场均衡价格的计算模型，设用m（m=1，2，…，m）辆配送车对i（i=1，2，…，n）个客户进行运输配送，每个客户持有的现金数额分别是A=｛e1，e2，…，en｝，必须支付配送车辆的服务 B=｛q1，q2，…，qm｝的费用，考虑如下一类对数收益函数:

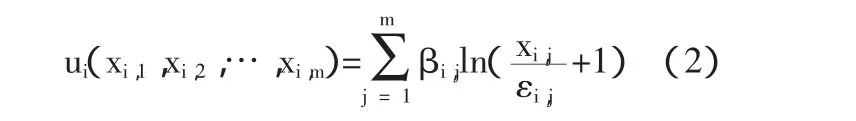
应用Lagrange乘子法，求解方程组后得:

这就可以得到配送中心的配送运输的最大收入为:

其等同于:

三、量子粒子群优化求解

（一）初始化种群。直接采用量子位的概率幅作为粒子（即配送车辆）当前位置的编码，其初始化编码的方案:

（二）解空间变换。量子位的每个概率幅对应解空间的优化变量，记粒子 Pj上第 i个量子位为［αij，βij］T，则相应的解空间变量为:

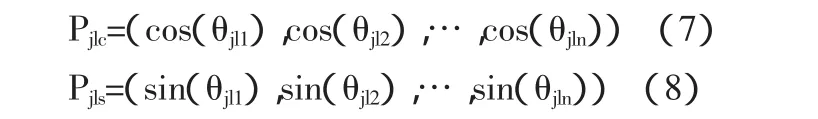
（三）粒子状态更新。粒子状态更新规则为:

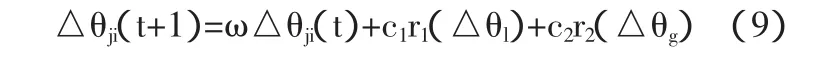
（四）变异处理。由量子非门实现变异操作过程。

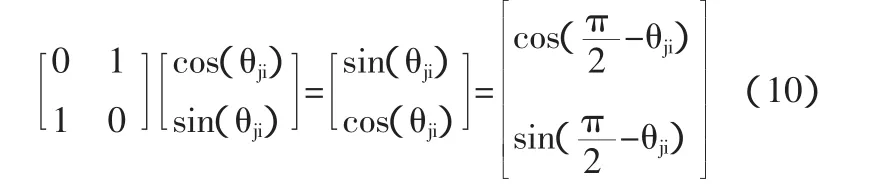
其中 j∈｛1，2，…，m｝，i∈｛1，2，…，n｝。

（五）粒子群的适应度。基于共赢的配送路径量子粒子群优化的适应度定义为:

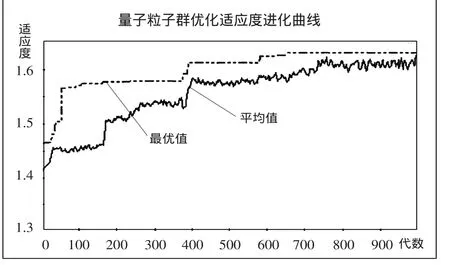
图1 量子粒子群优化适应度进化曲线

其中，VN表示使用的车辆数，VNmin表示已知使用的最小车辆数，VNmax表示已知使用的最大车辆数，D表示车辆行驶的总距离，Dmin表示车辆最小行驶距离，Dmax表示车辆最大行驶距离，WT表示总等待时间，WTmin表示前种群中最小等待时间，WTmax表示前种群中最大等待时间，而 ρ1，ρ2，ρ3，ρ4，ρ5表示权重，且 ρ1+ρ2+ρ3+ρ4+ρ5＝1。

四、求解优化算例

石药乐仁堂医药物流配送中心，其主要的业务是从事药品的零售配送。配送技术指标为:年工作时间为251天（每周五日工作制），每天工作8小时（一班制），药品预计年销量40万大箱，全省内零售户数为28，000户，一周配送一次，即平均每个工作日将配送4，800个零售户，用户提供详细零售户的布局情况。用基于共赢配送路径模型进行优化，进行了为期3个月的优化计算，图1是其适应度函数的进化曲线图。（图1）优化结果:优化前原配送车辆为70辆，优化后使用56辆；优化后的路径围绕配送中心成“花瓣形”，配送中心的综合运营成本大幅度下降，单件药品的综合运行成本降至0.16元，与实际运行的效果接近。

本文基于共赢机理去思考配送路径的优化问题，兼顾对顾客、对商家的利益，可以提高配送中心建设的科学性以及提高配送中心运营质量。

［1］G.B.Dantzig，J.H.Ramser，The Truck Dispatching Problem.1959.

［2］贾永基.车辆调度问题优化算法研究.上海交通大学博士学位论文，2004.

［3］Ning Chen，Xiaotie Deng，Xiaoming Sun.Andrew Chi-Chih Yao:Fisher Equil ibrium Price with a Class of Concave Uti lity Functions，ESA 2004.