用谐波小波包变换法提取GIS局部放电信号多尺度特征参数
2015-11-14张晓星
唐 炬 樊 雷 张晓星 刘 欣
(重庆大学输配电装备及系统安全与新技术国家重点实验室 重庆 400044)
1 引言
气体绝缘组合电器(Gas Insulated Switchgear,GIS)在生产制造和长期运行过程中,不可避免地会出现各种绝缘缺陷,导致不同程度的局部电场畸变,从而诱发局部放电(Partial Discharge,PD),使得设备绝缘性能进一步劣化甚至发生击穿的严重后果,威胁电力系统的安全稳定运行。对GIS实行PD在线监测有利于尽早地发现绝缘故障,可有效预防重大事故发生,并为合理制定GIS的状态检修策略提供依据。目前,检测GIS设备PD的方法主要包括:脉冲电流法、超高频法、超声波法、光学法、化学法等[1]。其中,由于超高频法具有现场安装方便、灵敏度高、抗干扰能力强等优点,在GIS设备PD在线监测中得到了广泛应用。
由于不同类型的绝缘缺陷对GIS设备的危害程度不同,所采取的检修策略也有所不同,因此,对绝缘缺陷的类型进行识别就显得尤为重要。由于GIS绝缘缺陷种类的多样性和现场监测环境的复杂性,单从检测得到的超高频(Ultra-High Frequency,UHF)PD信号本身出发,往往难以准确实现缺陷类型的判别。因此,需要对检测到的UHF PD信号进行特征提取,获得能够有效区分各类缺陷的特征量,从而实现缺陷类型的识别。有效的特征提取方法是进行缺陷识别的基础,特征量的选取直接影响识别结果的准确性。
目前,PD信号的特征提取方法主要分为两大类,一类是统计谱图法,通过采集多个工频周期的PD信号,构造二维或三维统计谱图,再从中提取统计特征[2-4]、分形特征[5,6]、数字图像特征[7,8]等特征参数。对UHF PD信号而言,若采用统计谱图法,其采样率要求高,数据量大,处理数据速度慢,不利于在线监测,而且构造统计谱图需要 PD的相位信息,但是在监测现场GIS高压一次侧的电压同步信号往往难以获得;另一类是波形分析法,通过采集单次UHF PD信号波形,提取信号的时域、频域或其他变换域特征[9-11]。这种方法数据量小,处理速度快,且不需要放电相位信息,但由于 PD脉冲激发的电磁波在传播过程中存在衰减和折反射,监测现场同时存在着严重的电磁干扰,传统的基于时域或频域的特征参数易受噪声污染,要准确提取 PD信号的特征参数比较困难。
小波变换具有良好的时频局部化分析能力,利用小波变换可以同时得到信号局部的时域和频域信息,获得能够更加精确和有效描述信号的多尺度特征参数,在PD信号特征提取中得到了广泛应用[10,11]。小波包变换(Wavelet Packet Transform,WPT)是在小波变换的基础上对高频部分作进一步分解,具有更高的频率分辨率,能对信号进行更精确细致的分析。然而,由于传统实小波对应的高、低通滤波器并非理想盒形滤波器,其幅频响应曲线存在交错频段,导致实小波包分解得到的子带间往往存在严重的频谱混叠和能量泄漏[12],因而从实小波包分解得到的子带中提取的多尺度特征参数不能精确描述PD信号的时频信息,不利于后续的分类识别。
谐波小波是在频域具有严格盒形频谱特性的复小波,谐波小波包分解得到的各子带间不存在频谱混叠和能量泄漏,子带信号能够精确描述原信号的时频特征,在生物医学信号处理[13]和机械故障诊断[14]领域得到了广泛应用。本文利用谐波小波包变换(Harmonic Wavelet Packet Transform,HWPT)对4种GIS典型缺陷的UHF PD信号进行处理,从UHF PD信号在时频域的复杂度和能量分布的差异出发,研究能够有效区分不同绝缘缺陷的多尺度特征参数,并采用支持向量机分类器实现缺陷类型识别。
2 谐波小波
2.1 谐波小波变换
Newland在1993年成功构造出在频域具有严格盒形频谱特性的谐波小波[15],其在频域的广义表达式为
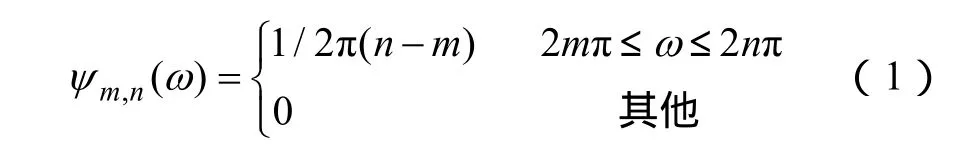
式(1)中尺度参数m、n∈R+且m<n,m、n决定了谐波小波频域支撑区间的长度。对ψm,n(ω)进行傅里叶逆变换,即得谐波小波的时域表达式
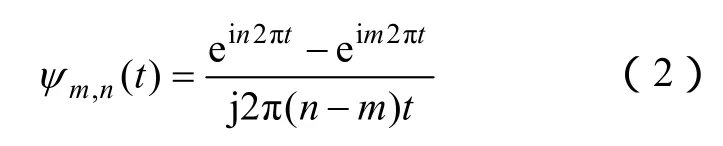
将ψm,n(t)以步长k/(m-n)进行平移,得到谐波小波时域的广义表达式[16]
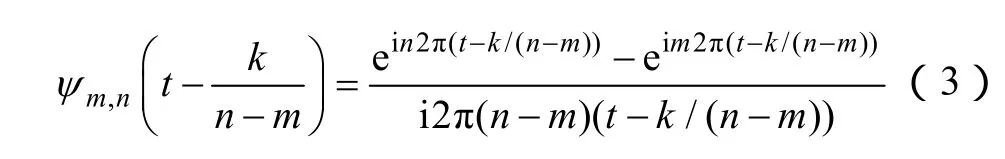
式中,k为平移参数;表示时域中心在k/(n-m),频域带宽为2π(n-m)的谐波小波。通过合理确定m,n的值,即可在不同层上以不同的分辨率对频率轴进行划分。当m=0,n=8,k=4和m=16,n=24,k=4时,谐波小波时域(实部和虚部)和频域波形如图1所示。Im(ψm,n(t))
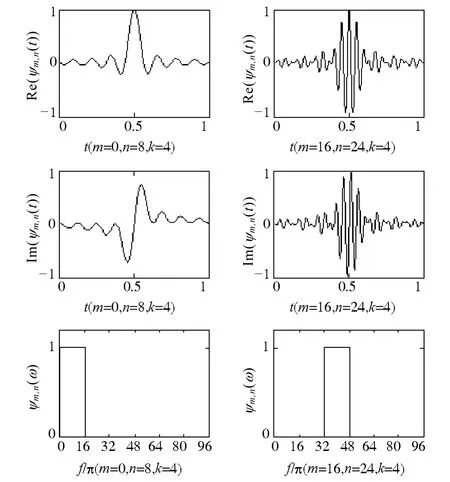
图1 谐波小波时域波形和频谱Fig.1 The waveforms and spectrum of the harmonic wavelet function
对给定信号f(t),其谐波小波变换可写为
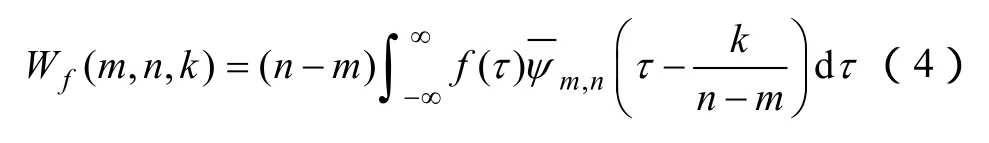
对式(4)作傅里叶变换,得到谐波小波变换的频域表达式为

由上述分析可见,谐波小波变换是一种基于FFT和IFFT的快速算法,与实现实小波变换的MALLAT算法不同,谐波小波变换不存在与滤波器多次卷积和二抽取采样过程,具有极高的计算效率。
2.2 谐波小波包变换
在式(3)中,随着m、n、k取值的不同,谐波小波进行伸缩和平移形成一组谐波小波基序列,m、n取值的不同对应着频率轴上不同分辨率的划分。若将第j(j∈Z+)层上各小波的分析频率带宽取为B=fh/2j,则尺度参数m、n需满足
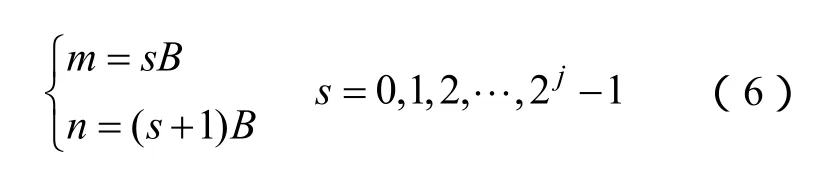
式中,fh为信号的最高分析截止频率。随着分解层数j的增大,即可由谐波小波包{ψm,n(t)}实现对信号整个频带的无限细分。
对一个给定长度为N的实数值离散信号f,具体操作如下:
(1)对离散信号f进行FFT,得到变换值(ω)。
(2)构造一棵完整的二叉树,根节点与频率序列ω={ 0,2π,…,k2π,…,Nf2π} 相对应,将频带进行二进划分,其中Nf为奈奎斯特频率。
(3)根据式(5)计算第j层各频段谐波小波变换的频域值(ω)。
(4)在二进划分下,将第j层每个子带的(ω)进行逆FFT变换,即获得相应子带的时域信号。
对实小波而言,以 Db小波为例,只有随着小波滤波器长度的增加,其幅频响应曲线才会逐渐趋向盒形,Db5和Db20小波滤波器的幅频响应曲线如图2所示,因而WPT不能实现频带的精确划分,分解得到的子带间往往存在严重的频谱混叠和能量泄漏。若采用WPT对UHF PD信号进行分解,得到的子带信号并不能真实准确地反应UHF PD信号局部频段内的时域信息,从各子带信号中提取的多尺度特征参数,必然会受子带间频谱混叠和能量泄漏的影响,导致特征量不能精确描述UHF PD信号所包含的信息,不利于后续缺陷类型的识别。
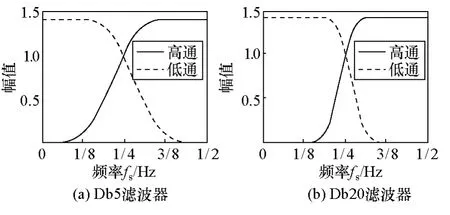
图2 滤波器幅频响应曲线Fig.2 The frequency response curve of the filter
谐波小波相对于一般的实小波而言,其最大的优点就是具有严格盒形的频谱,从而可以利用HWPT对时频面进行精确细致的划分,分解得到的子带间不存在频谱混叠和能量泄漏,从各子带信号中提取的多尺度参数能够精确描述UHF PD信号的时频特征。因此,本文采用HWPT对UHF PD信号进行处理。
3 特征量的选取
3.1 多尺度能量参数
由于不同类型的绝缘缺陷产生 PD的物理本质不同,会产生不同类型的放电脉冲,从而激发产生的 UHF电磁波的时域波形和频域能量分布必然也存在较大差异;而同种类型的绝缘缺陷放电的物理过程和放电脉冲激发的超高频电磁波具有较强的相似性。由于单一尺度的时域或频域特征参数易受外界干扰,因此,将时频域的多尺度能量分布特征作为区分不同类型缺陷的特征量。用 HWPT对 UHF PD信号进行多尺度分解,通过计算各子带信号的相对能量(Relative Energy,RE)值,即可得到 PD信号的多尺度能量特征参数。对一个给定离散UHF PD信号X(i),i=0,1,2,…,N-1,其计算步骤如下:
(1)将X(i)进行j层谐波小波包分解,得到 2j个不同频段范围的子信号序列,即Xk(i),k=1,2,…,2j;i=0,1,2,…,N-1。
(2)计算各子带信号Xk(i)的能量值,得到子带能量序列,即
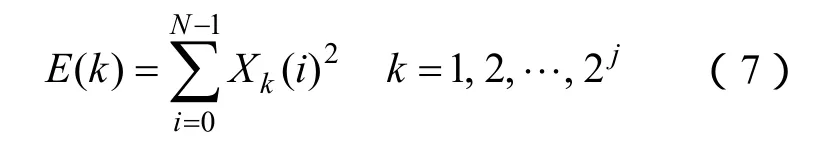
(3)对子带信号能量序列E(k)进行归一化处理,得到子带相对能量值序列,即

3.2 多尺度样本熵参数
UHF PD信号通常具有放电信号微弱、频带范围宽和非线性、非平稳等特性,传统的基于线性系统的特征提取方法不能有效提取 PD信号的非线性特征,而基于非线性动力学参数的特征提取方法更能反应信号的本质特征。在故障诊断中使用较多的非线性动力学参数有关联维数、最大Lyapunov指数[17]、各种熵[18]等。2000年 Richman提出的样本熵(Sample Entropy,SampEn)在近似熵的基础上进行了改进[19],作为对时间序列复杂度的一种度量,它对时间序列的长度依赖性小,并且具有较强的稳定性和抗噪性,在生物医学信号处理中得到了广泛应用[20]。
从物理学意义上讲,熵是能给系统的不确定程度以某种整体度量的量。由于不同的绝缘缺陷产生PD所对应物理系统的复杂度不同,因而UHF PD信号的熵值必然存在差异,可以通过计算谐波小波包分解后各子带信号的样本熵特征,来刻画时频面不同位置信号复杂度的分布。相对于仅采用原始UHF PD信号的样本熵作为特征量单一尺度分析而言,谐波小波包分解的特征提取方法能在多个尺度内对信号进行更加细致和精确的分析,从而挖掘不同缺陷UHF PD信号的深层次信息,有利于后续缺陷类型的识别。对一个给定离散 UHF PD信号 (),Xii=0,1,2,,1N-…,其操作过程如下:
(1)对X(i)进行j层谐波小波包分解,得到 2j个不同频段范围的子信号序列Xk(i),k=1,2,…,2j;i=0,1,2,…,N-1。
(2)计算各子带信号Xk(i)的样本熵值,得到子带样本熵序列SampEn(),1,2,,2j kk=… 。
样本熵的计算方法参考文献[21],样本熵的值与模式维数m和相似容限r的取值有关,根据Pincus的研究结果[22],m=1或m=2,r=0.1~0.25Std(Std是原始数据x(i),i=0,1,2,…,N-1的标准差)计算得到的样本熵具有较为合理的统计特性。因此,本文选择m=2,r=0.2Std。
4 数据采集与处理
4.1 人工绝缘缺陷模型局部放电试验
根据GIS设备绝缘缺陷的放电形式和特点,在实验室中设计了 4种人工物理绝缘缺陷模型[23]来模拟GIS内部的局部放电,分别是:金属突出物缺陷,简称N(needle)类缺陷;自由金属微粒缺陷,简称P(particle)类缺陷;绝缘子表面金属污秽缺陷,简称 M(metal)类缺陷;气隙缺陷,简称 G(gap)类缺陷。
将上述4种人工物理绝缘缺陷模型分别置于研制的 GIS模拟装置中[24],并充以 0.5MPa的 SF6和N2的混合气体(体积比4:1),超高频传感器采用研制的微带天线[25],中心频率为 390MHz,驻波比小于2的绝对带宽为340~440MHz,进行数据采集的示波器为泰克 7100(模拟带宽 1GHz,最大采样率20GS/s,存储深度48MB)。实测中,信号经频带为0.15~1GHz的有源滤波器传输至示波器,4种缺陷分别在不同条件下(改变施加电压等级、传感器位置、缺陷形状)采集UHF PD信号,采样率为5GHz,每类每种条件下采集50组有效放电样本,最终,得到4类缺陷PD样本数据各450组。图3所示为微带天线实测的4种缺陷模型的UHF PD信号。
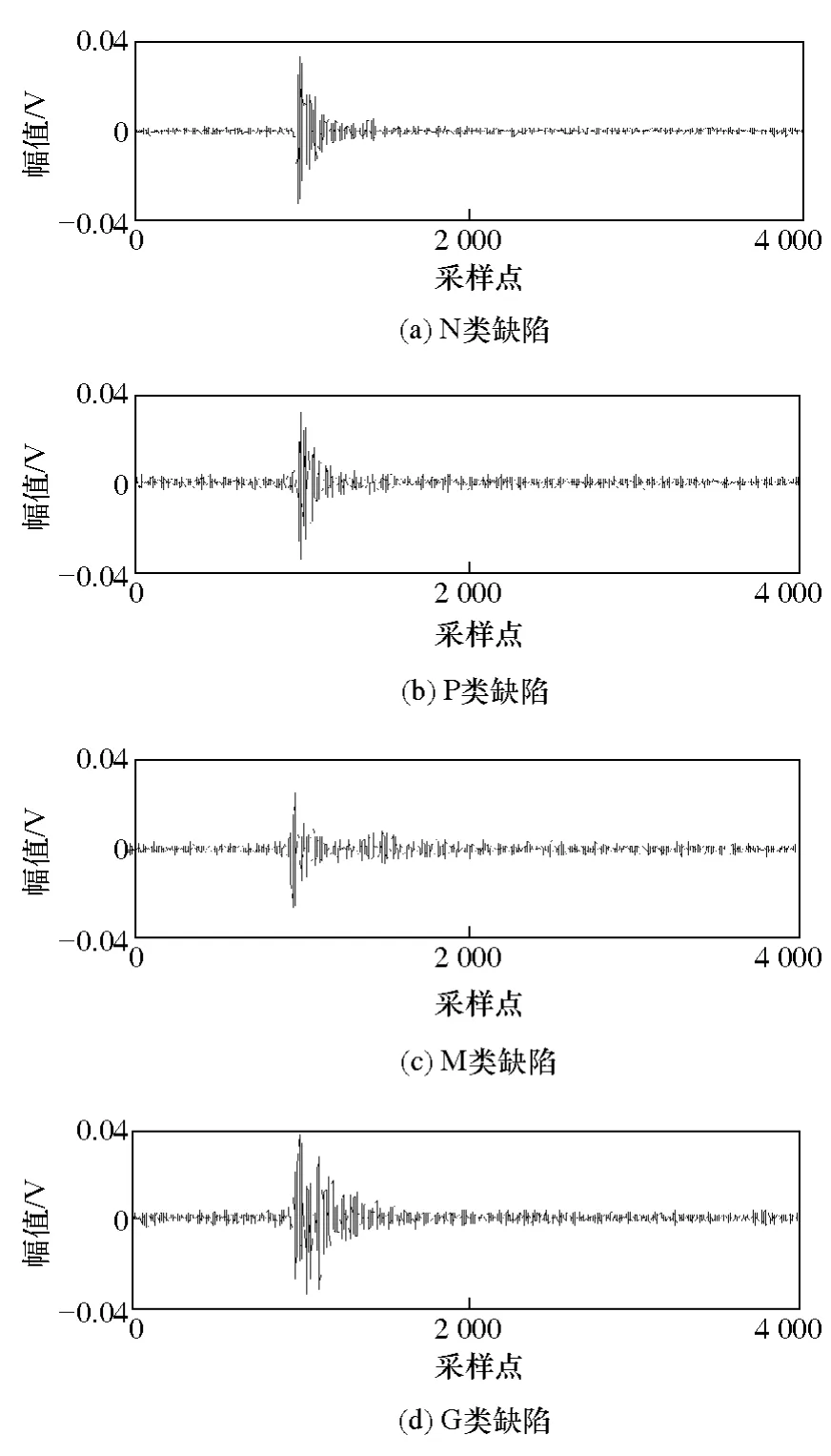
图3 4种典型绝缘缺陷的UHF PD信号Fig.3 The UHF PD signal of the four typical insulation defect
4.2 特征提取
对采集到的4种缺陷的UHF PD信号进行5层谐波小波包分解,共得到32个子带,由于示波器模拟带宽为 1GHz,同时为了排除低频干扰对特征提取精度的影响,选取频带范围在0.15~1GHz内的共11个子带作为特征子带,计算各子带的相对能量和样本熵。
从4种缺陷各自的UHF PD信号样本库中分别随机选取100组数据作为训练样本,每类缺陷剩余的350组数据作为测试样本,按照图4所示的步骤完成对所有UHF PD信号的特征提取,得到4种缺陷UHF PD信号特征库。经统计分析,得到4种缺陷UHF PD信号多尺度能量特征和多尺度样本熵特征的95%置信区间,如图5和图6所示。
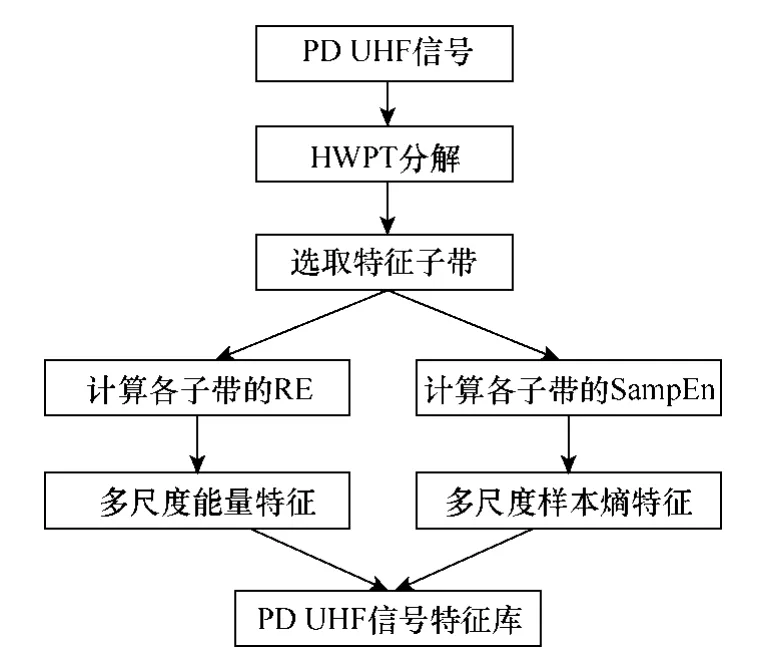
图4 特征提取流程图Fig.4 The flowchart of feature extraction

图5 多尺度能量参数的95%置信区间Fig.5 The 95% confidence interval of the multi-scale energy parameters

图6 多尺度样本熵参数的95%置信区间Fig.6 The 95% confidence interval of the multi-scale sample entropy parameters
由图5可知,N类和P类缺陷UHF PD信号的能量主要集中在400MHz以上的频段,而M类和G类缺陷UHF PD信号的能量主要集中在400MHz以下的频段。由于不同绝缘缺陷产生的放电脉冲的波形和陡度不同,从而导致激发的UHF信号能量分布具有较大的差异,说明利用多尺度能量特征来进行缺陷类型识别是可行的。
由图 6可知,4种绝缘缺陷特征子带的样本熵序列也存在较大差异,主要表现在信号能量集中的子带内。P类和M类缺陷计算得到的样本熵值在部分子带内明显远高于N类和G类缺陷,说明这两种类型的放电所对应的物理系统的复杂度更高,放电过程中的随机性也更大。因此,利用多尺度样本熵来区分不同的绝缘缺陷是可行的。
从各子带特征量分布的离散程度来看,N类缺陷计算得到的各子带特征量分布较为集中,而P类、M类和G类缺陷部分子带内所提取的特征量波动较大。由于N类缺陷的放电过程较为稳定,采集到的UHF PD信号波形变化不大,所以提取的子带特征量波动较小;自由金属微粒缺陷(P类)在加压过程中金属微粒存在静止、移动、跳动等多种状态,放电过程不稳定,UHF PD信号波形变化较大,导致部分子带内的特征值波动较大;对绝缘子表面金属污秽缺陷(M类)而言,由于放电通道在绝缘子表面的发展不够稳定,具有较大的随机性,并且在多次放电后,绝缘子表面出现局部严重炭化现象,导致采集到的UHF PD信号波形存在较大波动;而气隙缺陷(G类)由于产生气隙的绝缘子在多次实验中出现了数次击穿,且表面局部出现轻微炭化现象,采集到的UHF PD信号波形也出现了一定的波动。
4.3 缺陷类型识别
UHF PD信号的识别采用支持向量机(Support Vector Machine,SVM)分类器实现,SVM是在统计学习理论基础上发展起来的一种新型机器学习方法,它避免了人工神经网络方法的网络结构选择、过学习和欠学习及局部极小等问题,在学习精度和泛化能力间取得了良好的平衡,适用于求解高维、小样本、非线性情况下的模式分类和回归分析等问题[26]。
根据 Hsu and Lin[27]的研究结果,选用“一对一”的 SVM 识别方法进行四类缺陷类型识别。实验中 SVM 的核函数选择最常用的高斯径向基核函数,其表达式为

式中,σ为控制核函数高度与宽度的参数,对于线性不可分情况,引入惩罚因子C来控制错误分类。参数取值为 2σ2=N,N为输入数据集特征属性的维数,惩罚因子C=10。从每类缺陷的特征库中随机选取100组样本数据进行训练,并计算其余样本的识别正确率,识别结果如下表所示,表中单位为%。

表 UHF PD信号的识别准确率Tab. The recognition accuracy of the UHF PD signal
以Db20小波为母小波,采用WPT来提取相同的特征量,对比识别结果发现,对于相同的多尺度特征参数,采用 HWPT分解得到的识别率明显高于采用WPT分解方法。这是由于HWPT分解得到的子带间不存在频谱混叠和能量泄漏,获取的多尺度特征量能够更加精确地描述原始信号的时频特征,因而取得了更好的识别效果。多尺度能量特征和多尺度样本熵特征都取得了较好的识别结果,平均识别率高于90%。
5 结论
(1)谐波小波具有严格的盒形频谱,利用谐波小波包可以实现频带的精确划分,克服了实小波包分解子带间存在频谱混叠和能量泄漏的缺点,分解得到的子带信号能够更加细致和精确地描述 UHF PD信号的时频信息。
(2)不同类型的绝缘缺陷产生的UHF PD信号具有不同的时频分布特性,提出的多尺度能量和多尺度样本熵特征参数能够有效刻画UHF PD信号在时频域的能量分布和复杂度信息,具有较好的稳定性和抗干扰能力。
(3)对4种典型放电模型产生的UHF PD信号识别结果表明,基于HWPT的多尺度能量和多尺度样本熵特征参数均能有效识别4种绝缘缺陷,平均识别准确率高于 90%,明显优于基于 WPT的特征提取方法。
[1] 钱勇,黄成军,江秀臣,等. 基于超高频法的 GIS局部放电在线监测研究现状及展望[J]. 电网技术,2005,29(1): 40-43.
Qian Yong,Huang Chengjun,Jiang Xiuchen,et al.Present situation and prospect of ultrahigh frequency method based research of on-line monitoring of partial discharge in gas insulated switchgear[J]. Power System Technology,2005,29(1): 40-43.
[2] 王辉,郑文栋,黄成军,等. GK模糊分类算法在GIS局部放电模式识别中的应用[J]. 电力系统保护与控制,2011,39(17): 50-54.
Wang Hui,Zheng Wendong,Huang Chengjun,et al.Application of Gustafson-Kessel fuzzy classification algorithm in the pattern recognition of partial discharge for GIS[J]. Power System Protection and Control,2011,39(17): 50-54.
[3] 姚林鹏,徐颖敏,钱勇,等. 基于关联规则的 XLPE电缆局部放电模糊识别研究[J]. 电工技术学报,2012,27(5):92-98.
Yao Linpeng,Xu Yingmin,Qian Yong,et al. Fuzzy pattern recognition of partial discharge in XLPE cable based on association rule[J]. Transactions of China Electrotechnical Society,2012,27(5): 92-98.
[4] 姚林鹏,王辉,钱勇,等. 基于半监督学习的 XLPE电缆局部放电模式识别研究[J]. 电力系统保护与控制,2011,39(14): 40-46.
Yao Linpeng,Wang Hui,Qian Yong,et al. Pattern recognition of partial discharge in XLPE cable based on semi supervised learning[J]. Power System Protection and Control,2011,39(14): 40-46.
[5] 张晓星,唐炬,孙才新,等. 基于多重分形维数的GIS局部放电模式识别[J]. 仪器仪表学报,2007,28(4): 597-602.
Zhang Xiaoxing,Tang Ju,Sun Caixin,et al. PD pattern recognition based on multi-fractal dimensions in GIS[J]. Chinese Journal of Scientific Instrument,2007,28(4): 597-602.
[6] 任先文,薛雷,宋阳,等. 基于分形特征的最小二乘支持向量机局部放电模式识别[J]. 电力系统保护与控制,2011,39(14): 143-147.
Ren Xianwen,Xue Lei,Song Yang,et al. The pattern recognition of partial discharge based on fractal characteristics using LS-SVM[J]. Power System Protection and Control,2011,39(14): 143-147.
[7] 唐炬,魏刚,李伟,等. 基于双向二维最大间距准则的局部放电灰度图像特征提取[J]. 电网技术,2011,35(3): 129-134.
Tang Ju,Wei Gang,Li Wei,et al. Partial discharge gray image feature extraction based on Bi-directional Two-Dimensional maximum margin criterion[J]. Power System Technology,2011,35(3): 129-134.
[8] 刘云鹏,律方成,李成榕. 局部放电灰度图像数学形态谱的研究[J]. 中国电机工程学报,2004,24(5):179-183.
Liu Yunpeng,Lü Fangcheng,Li Chengrong. Study on pattern spectrum of partial discharge grayscale image[J]. Proceedings of the CSEE,2004,24(5): 179-183.
[9] Chang C,Chang C S,Jin J,et al. Source classification of partial discharge for gas insulated substation using waveshape pattern recognition[J]. IEEE Transactions on Dielectrics and Electrical Insulation,2005,12(2):374-386.
[10] 李剑,王小维,金卓睿,等. 变压器局部放电超高频信号多尺度网格维数的提取与识别[J]. 电网技术,2010,34(2): 159-163.
Li Jian,Wang Xiaowei,Jin Zhuorui,et al. Multi-scale grid dimension extraction and recognition of ultra-high frequency signals of transformer partial discharge[J].Power System Technology,2010,34(2): 159-163.
[11] 唐炬,谢颜斌,周倩,等. 基于最优小波包变换与核主分量分析的局部放电信号特征提取[J]. 电工技术学报,2010,25(9): 35-40.
Tang Ju,Xie Yanbin,Zhou Qian,et al. Feature extraction for partial discharge signals based on the optimal wavelet packet basis transform and kernel principal component analysis[J]. Transactions of China Electrotechnical Society,2010,25(9): 35-40.
[12] 李辉,丁桦. 一种抗混叠和失真的小波包信号分解与重构算法[J]. 科学技术与工程,2008,8(20):5580-5588.
Li Hui,Ding Hua. Anti-aliasing and anti-distortion algorithm for signal decomposition and reconstruction based on wavelet package analysis[J]. Science Technology and Engineering,2008,8(20): 5580-5588.
[13] Wang G,Yan Z,Hu X,et al. Classification of surface EMG signals using harmonic wavelet packet transform[J]. Physiological measurement,2006,27(12): 1255-1267.
[14] Yan R,Gao R X. An efficient approach to machine health diagnosis based on harmonic wavelet packet transform[J]. Robotics and Computer-Integrated Manufacturing,2005,21(4): 291-301.
[15] Newland D E. Harmonic wavelet analysis[J]. Procee-dings of the Royal Society of London. 1993,443(10):203-205.
[16] Newland D E. Harmonic and musical wavelets[J].Proceedings of the Royal Society of London. 1994,443(10): 605-620.
[17] 王炳成,任朝晖,闻邦椿. 基于非线性多参数的旋转机械故障诊断方法[J]. 机械工程学报,2012,48(5): 63-69.
Wang Bingcheng,Ren Chaohui,Wen Bangchun.Fault diagnoses method of rotating machines based on nonlinear multi-parameters[J]. Journal of Mechanical Engineering,2012,48(5): 63-69.
[18] 陈继开,周志宇,李浩昱,等. 快速小波熵输电系统暂态信号特征提取研究[J]. 电工技术学报,2012,27(12): 219-225.
Chen Jikai,Zhou Zhiyu,Li Haoyu,et al. Study of fast wavelet entropy’s application in feature extraction of transient signals in transmission line[J]. Transactions of China Electrotechnical Society,2012,27(12): 219-225.
[19] Richman J S,Moorman J R. Physiological time-series analysis using approximate entropy and sample entropy[J]. American Journal of Physiology-Heart and Circulatory Physiology,2000,278(6): H2039-H2049.
[20] Al-Angari H M,Sahakian A V. Use of sample entropy approach to study heart rate variability in obstructive sleep apnea syndrome[J]. IEEE Transactions on Biomedical Engineering,2007,54(10): 1900-1904.
[21] Alcaraz R,Rieta J J. A review on sample entropy applications for the non-invasive analysis of atrial fibrillation electrocardiograms[J]. Biomedical Signal Processing and Control,2010,5(1): 1-14.
[22] Pincus S M. Assessing serial irregularity and its implications for health[J]. Annals of the New York Academy of Sciences,2001,954(1): 245-267.
[23] 张晓星,唐炬,孙才新,等. 基于核统计不相关最优鉴别矢量集的GIS局部放电模式识别[J]. 电工技术学报,2008,23(9): 111-117.
Zhang Xiaoxing,Tang Ju,Sun Caixin,et al. PD pattern recognition based on kernel statistical uncorrelated optimum discriminant vectors in GIS[J]. Transactions of China Electrotechnical Society,2008,23(9): 111-117.
[24] 唐炬,欧阳有鹏,王存超,等. 模拟气体绝缘组合电器产生不同局部放电的试验装置研制[J]. 重庆大学学报,2010,33(11): 39-45.
Tang Ju,Ouyang Youpeng,Wang Cunchao,et al.Study on the testing device for simulating the partial discharges of different defects in gas insulated switchgear[J]. Chinese Journal of Chongqing University,2010,33(11): 39-45.
[25] 张晓星,唐炬,彭文雄,等. GIS局部放电检测的微带贴片天线研究[J]. 仪器仪表学报,2006,27(12):1595-1599.
Zhang Xiaoxing,Tang Ju,Peng Wenxiong,et al.Study on the outer UHF microstrip patch antenna for partial discharge detection in GIS[J]. Chinese Journal of Scientific Instrument,2006,27(12): 1595-1599.
[26] Vapnik V N. 统计学习理论的本质[M]. 张学工,译北京: 清华大学出版社,2000.
[27] Hsu C W,Lin C J. A comparison of methods for multiclass support vector machines[J]. IEEE Transactions on Neural Networks,2002,13(2): 415-425.
