发输电检修与机组组合联合决策的Benders分解方法
2015-11-14李本新韩学山
李本新 韩学山
(山东大学电网智能化调度与控制教育部重点实验室 济南 250061)
1 引言
发电、输电等环节的设备检修、机组组合是电力系统运行方式决策中关键而核心的任务。一直以来,检修决策往往在年度时间框架内进行,机组起停决策往往在日、周时间框架内进行。这两个决策问题在面临实施时,必然存在衔接与协调的问题,随着电网设备状态检修技术的日益成熟,使电力系统设备检修决策问题和机组起停决策问题间越来越存在密切的关联,有机进行联合优化决策会带来更大效益,对其深入研究具有重要意义[1-5]。
在以往研究中,发输电检修与机组组合的联合决策(Generation and Transmission Maintenance Scheduling with Unit Commitment,GTMS_UC),往往在检修决策时,通过评估运行可靠性间接考虑其对电网运行的影响,其研究大致可分为三个方面:一是直接将可靠性纳入决策目标,以确定性或概率方法建立某种可靠性准则,以此构建优化的数学模型[6-9];二是追求检修、运行的成本最小,将可靠性指标作为约束条件构造数学优化模型。该类研究中,Benders分解方法[10]得到广泛应用[11-18]。其中,文献[11,12]首先将电网约束纳入机组检修模型中,但未涉及输电设备检修。文献[13-17]对发、输电设备的联合检修决策进行研究。文献[18]的主要贡献在于将检修模型中的运行约束用近似的直流潮流进行建模,替代以往的线性传输(不考虑KVL)模型,使其更接近电网运行的物理规律;三是以可靠性作为决策目标,以电网运行的经济规律为约束条件,构造更为复杂的优化数学模型。如文献[19]针对电力市场环境下输电设备检修计划决策,建立了主从两层规划模型,上层以最大化电网传输裕度为目标,决策检修计划,下层以决策的检修计划作为输入,在满足电网传输制约的前提下最小化市场出清价格,并以约束的形式附着在上层优化问题中,最后基于线性规划的强对偶原理转换模型,使其具有可解性。相对而言,第I类研究模型简单,易于直接求解,但经济性与可靠性间的矛盾未予协调;第 II类研究模型复杂,必须实施分解协调的策略才能求解,但经济性与可靠性间的矛盾得到协调。第 III类研究,虽然经济性与可靠性间的矛盾得到协调,但其求解方法复杂,难以应用于实际电网。
总体而言,上述研究,对检修与运行协调决策的问题,通过处理安全、可靠及经济间的矛盾的思想是正确的,但因为考虑不同时间级间的关联而出现顾此失彼的现象还是难免的。对此,文献[20]从长期的检修计划决策与短期的发电计划决策在研究周期及时段划分方面的差异性出发,以电网的最小备用作为牵连指标,建立了检修与运行滚动决策的协调优化模型。在此基础上,文献[21]就检修与运行协调决策的问题进行了实质性的研究,该研究以成本最小为目标,同时考虑发、输电设备检修及机组组合,并给出通过 Benders分解法予以求解的总体方法,其特点在于:一是将问题需满足的时段划分方式与机组组合相对应;二是将问题前瞻的时间尺度对应在发输电设备检修的时间跨度上。由此,此文使检修与运行的协调进入到更细致的阶段,但依然侧重在数学优化算法的处理上,对其协调决策的机理尚缺乏足够、必要的分析,致使算法有其复杂性。解决实际工程问题,至少要回答两个问题:一是检修决策量与运行决策量在什么情景下产生关联;二是检修与运行同时决策在时空关联的公共区间如何识别。
由此,在前人工作基础上,本文提出发输电检修与机组组合联合决策的 Benders分解方法,把原问题分解为主问题、辅助问题以及潮流子问题,主问题在检修与运行关联的公共区间决策发、输电设备检修计划及机组运行计划;辅助问题一方面在非关联区间对主问题中的输电设备检修计划进行修正,另一方面对检修与运行在时空关联的公共区间进行识别;潮流子问题则对上述的决策结果进行潮流安全校验,建立检修决策量与运行决策量的牵连。按此方法,可使复杂电网求解更有效。
2 GTMS_UC模型
2.1 目标函数
由于研究针对短期,检修费用基本不随时间变化,故以研究周期内电网运行费用最小为决策目标,即
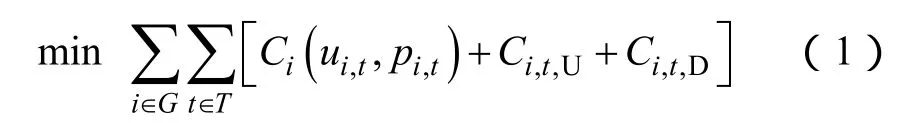
式中,G为发电机组集合;T为研究周期内划分的时段集合;Ci(ui,t,pi,t)为机组i的输出功率特性;pi,t、ui,t分别为机组i在t时段的有功输出功率和起停状态(0表示停机,1表示投运);Ci,t,U、Ci,t,D分别为机组i在t时段的起动和停机费用。
2.2 约束条件
约束分为如下三类。
(1)机组组合与机组检修相关约束
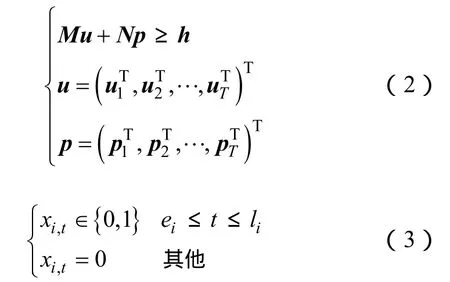

式中,ut、pt(t=1,2,···,T)分别为ui,t、pi,t(∀i)构成的列向量;xi,t为机组i在t时段的检修状态(停运检修时为1;否则为0),由xi,t(i∀)构成的列向量记为xt;qi,t为引入的辅助变量;ei、li分别为机组i检修时间窗口的起始与终止时间;JG,i为机组i检修持续时间;为机组i在时段t检修对资源k的需求量;Uk(t)为时段t资源k的可用量;Uk为前瞻周期内资源k的总量;M、N、h分别为常系数矩阵或向量。式(2)为机组组合相关约束,采用文献[22]的方式;式(3)表示机组检修必须安排在检修时间窗口内;式(4)表示机组检修延续时间约束;式(5)表示机组检修资源约束,其中的第一式表示每时段检修资源约束,第二式表示前瞻研究周期内检修资源总量约束;式(6)表示机组检修状态与起停状态间的牵连约束。
(2)输电检修相关约束

式中,L为待检修的输电设备集合;yℓ,t为输电设备ℓ在t时段的检修状态(0表示运行,1表示检修),由yℓ,t(∀ℓ)构成的列向量记为yt;rℓ,t为引入的辅助变量;eℓ、lℓ分别为输电设备ℓ检修时间窗口的起始与终止时间;Jℓ为输电设备ℓ检修持续时间;为输电设备ℓ在时段t检修对资源k的需求量。与式(3)~式(5)类似,式(7)表示输电设备检修必须安排在检修时间窗口内;式(8)表示输电设备检修延续时间约束;式(9)表示输电设备检修资源约束。
(3)潮流约束
以直流潮流为假设条件,电网潮流约束可表示为

式中,di,t为负荷i在t时段的有功功率;ik∈表示与节点k相关联的机组或负荷i;,tfℓ为输电设备ℓ在t时段有功功率传输;(),otθℓ、(),dtθℓ分别为输电设备ℓ首、末节点在t时段的相角;,tbℓ为输电设备ℓ的电纳;,maxfℓ为输电设备ℓ有功功率传输限值;ζ为很大的正数(惩罚系数)。式(10)、式(11)表示电网中的潮流必须同时满足KCL、KVL定律,式(12)表示输电设备有功传输能力约束。
由式(1)~式(12)构成的模型即为GTMS_UC模型。可见,由于该模型研究周期(前瞻时间)内必须与发、输电设备检修要求相符合,时段划分中每时段延续时间必须与机组组合相符合,因此是(空间和时间关联)复杂的优化数学模型。若不采用有效措施,对复杂大电网求解是难以进行的。
3 基于Benders分解的求解方法
3.1 潮流子问题求解过程
当主问题中的pt、yt给定,剩下的就是校验电网潮流约束是否满足。为此,∀t,构建由式(13)~式(17)所示潮流子问题。
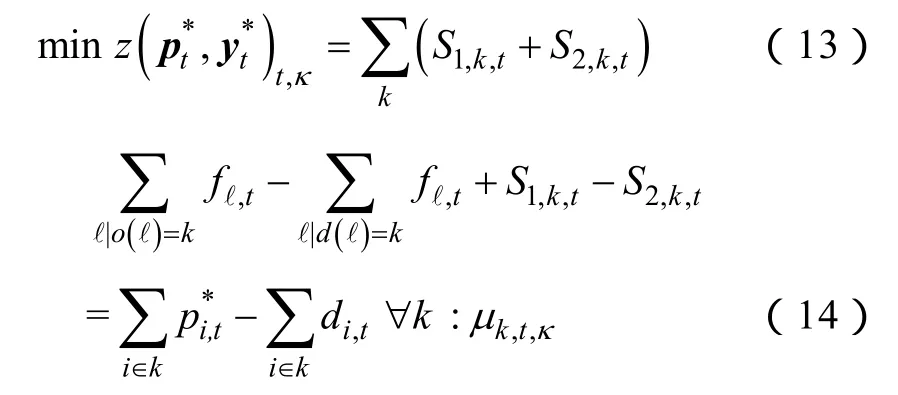
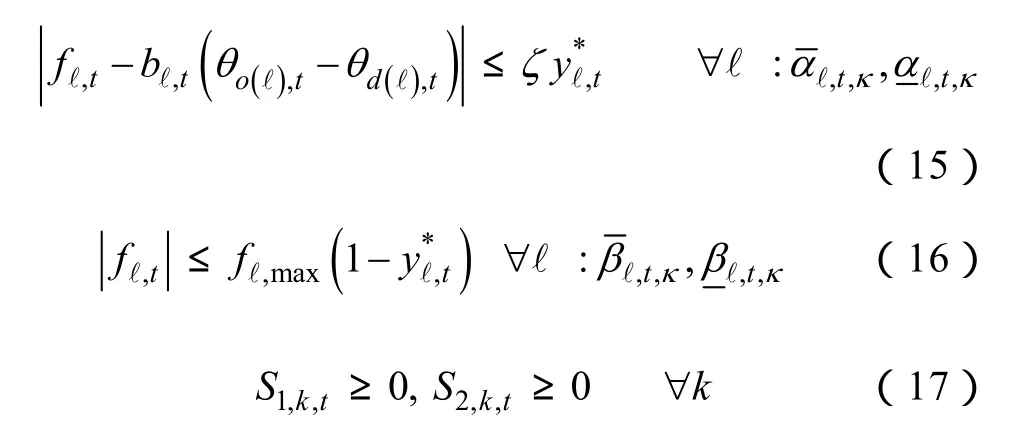
式中,1,,ktS、2,,ktS为引入的松弛变量,其作用在于当电网传输制约起作用时,通过松弛节点有功平衡约束,保证子问题有解,同时在问题间起衔接与协调的纽带作用;,,ktκμ、为对偶变量;、为牵连变量,来自主问题,且在潮流子问题处理过程中保持不变,视为参量,由此使潮流子问题变为凸优化问题。
GTMS_UC模型由于采用的负荷模式较为精细,使潮流子问题数众多,在迭代过程中,如果针对每一潮流子问题均进行优化以判别电网潮流制约是否满足,无疑会增加计算量。而且,在迭代过程中,发电方式发生变化的时段并不多、每一时段输电设备检修组合状态亦有限,由此,本文基于模式识别的思想,对潮流子问题集进行有效筛选,以缩减待优化的潮流子问题数。
基于模式识别思想,∀t,本文称单个有序数组(、)为 1个潮流子问题模式。若该模式下潮流子问题可行,则该模式为子问题可行模式,由子问题可行模式构成的集合称为子问题可行模式集,记为FSt。
按上述,基于模式识别思想的子问题集缩减可概括为:∀t,若潮流子问题模式(、)∈FSt,则该潮流子问题满足电网潮流约束,无需优化。否则,需通过数学优化的手段校验其可行性。
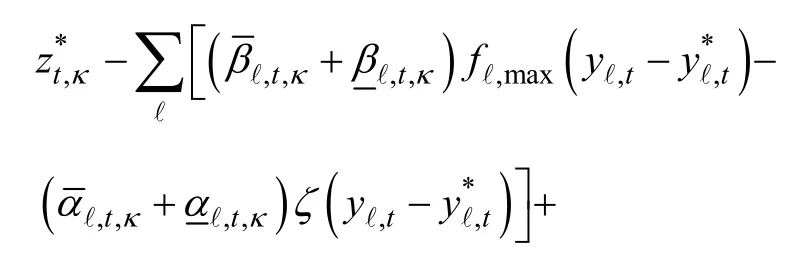
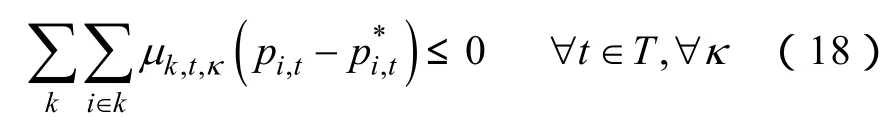
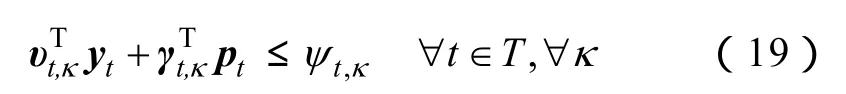
式中,,tκυ、tκ,γ为常系数列向量;,tκψ为常数,是标量。
3.2 主问题求解过程
由GTMS_UC模型可知,潮流约束中既包含与机组运行有关的决策量,又包含与输电设备检修相关的决策量,是二者的关联约束。若将该关联约束解耦,GTMS_UC模型可转化为规模相对较小的发电子问题和输电子问题。按此,基于拉格朗日松弛技术,建立主问题分解与协调的求解过程。当然,为了解耦的有效性,在解耦过程中,潮流约束不再是式(10)~式(12)的形式,而是替换为与其等价的式(19)所示的对偶形式。
3.2.1主问题的分解
(1)发电子问题。由式(2)~式(6),再补充式(20),即构成发电子问题。
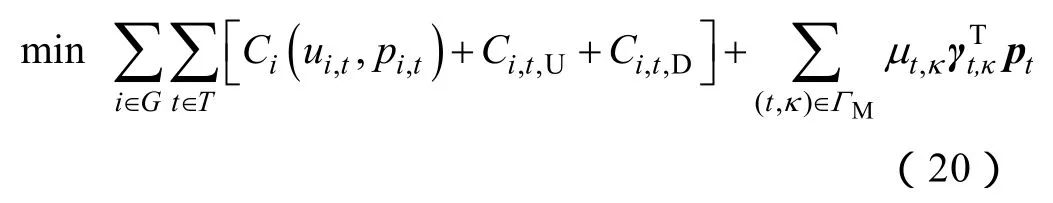
式中,ΓM为输电检修时间窗口内的割约束集合;μt,κ为与关联约束对应的乘子;γt,κ来自于式(19)。
(2)输电子问题。由式(7)~式(9)及补充的式(21),即构成输电子问题。
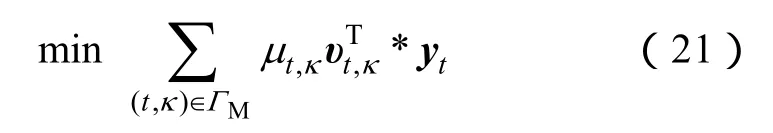
式中,,tκυ来自于式(19)。
手机作为社交工具展示了大众的一般生活状态。其中的微信、美图秀秀等每一个App,都聚集着数量巨大的商机族群,场景成了虚实交互融合的核心,产品即变成了场景。
3.2.2主问题协调求解框架
按拉格朗日松弛技术,GTMS_UC主问题协调求解框架如图1所示。图1中,乘子,tκμ修正按梯度法予以进行[23]。
3.3 辅助问题
按式(19),割约束集合是检修决策量yt与运行决策量pt的线性组合,其含义就是在、基础上对电网运行方式(或)进行微调,从而使潮流子问题可行。在调整过程中,检修决策量yt与运行决策量pt显现不同的作用机理:前者通过电网拓扑结构的调整消除潮流越限,如能消除,不会引起目标函数的改变,否则,将经由电网潮流约束间接引起目标函数的增加;后者侧重于发电方式的调整,由于目标函数是发电方式的显式表达,其改变将直接引起目标函数的增加。也就是说,当主问题的解与潮流子问题有冲突时,若能通过检修决策量的调整使冲突消除,则只需在由yt构成的低维区间修正检修计划即可,此时,检修决策量与运行决策量无矛盾,二者是非关联的;否则,需将割约束附着到主问题中,在由(xt,ut,pt,yt)构成的高维区间进行求解。此时,检修决策量与运行决策量存在矛盾,二者是关联的。
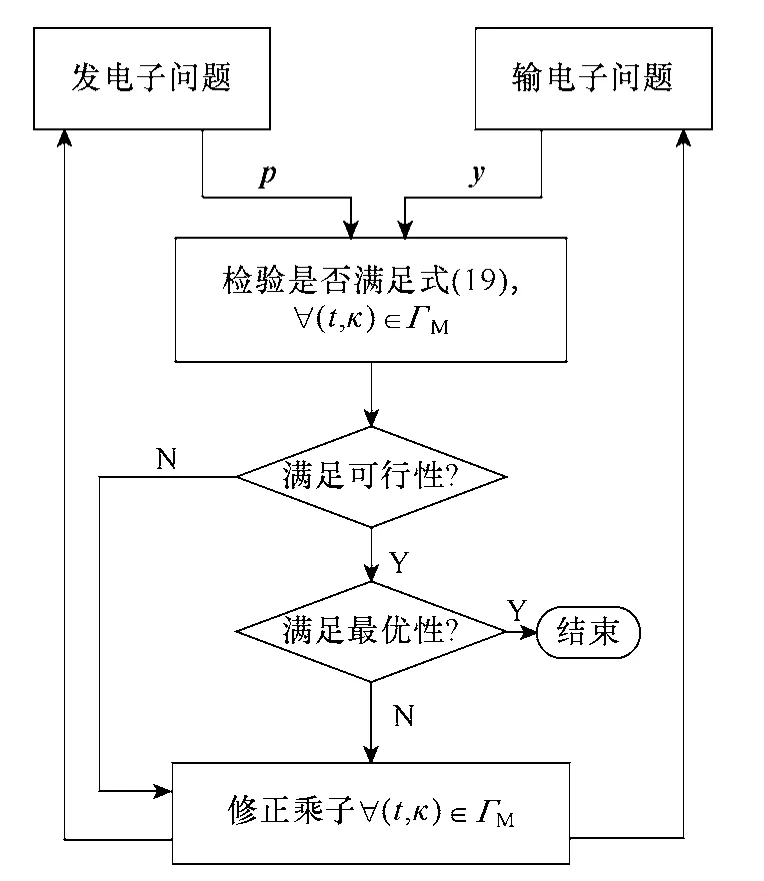
图1 GTMS_UC主问题协调求解框架Fig.1 Framework of coordination in main problem of GTMS_UC
基于上述输电设备检修与机组运行间的关联机制,在主问题、潮流子问题基础上构建由式(7)~式(9)、式(22)~式(24)所示辅助问题。

式(23)表示对上一次迭代产生的割约束进行松弛;式(24)表示剩余的割约束集合;Ωnew为与辅助问题邻近的迭代过程;Ωold为其他迭代过程构成的集合;,tsκ为引入的松弛变量,其作用在于当式(23)起作用时,以松弛变量暂时缓解这一制约,使辅助问题有解,同时起识别关联机制的作用。也就是说,当w*>0时,输电检修与机组运行存在矛盾,需在二者关联的高维区间决策;否则,只需在非关联的低维区间修正输电设备检修计划即可。
需要说明的是,引入辅助问题后,主问题中的割约束来源变为两类:一类是主问题的决策结果代入潮流子问题,所产生的检修与运行间的牵连;另一类是辅助问题的决策结果代入潮流子问题,产生的检修与运行间的牵连。
3.4 解算总流程
按上述对GTMS_UC模型分解处理后,解算总流程如下:
(1)初始化参数,∀t,置FSt=∅。
(2)求解初始主问题,确定电网初始运行方式。
(3)∀t∈T,判断潮流子问题模式是否是FSt中的元素,若是,不优化;否则,求解潮流子问题,并将潮流子问题可行模式追加到FSt中。求解后,若潮流子问题集存在不可行的情况,建立式(19)所示割约束,并追加到割约束集合,记为Γ,对其中满足t∈TM割约束归到ΓM中。若潮流子问题均可行,输出计算结果,结束计算。
(4)步骤(3)中,若ΓM无新增约束,则进入(7)。
(5)求解辅助问题,使ΓM中的约束得到满足,若不能满足,进入(7)。
(6)∀t∈TM,判断子问题模式是否是FSt中的元素,若是,不优化;否则,求解子问题并将子问题可行模式追加到FSt中。求解后,若子问题集存在不可行的情况,将新产生的割约束追加到ΓM、Γ中,返回(5);若不存在不可行的情况,且Γ-ΓM无新增约束,则输出计算结果,结束计算。
(7)修正主问题,使Γ中的约束得到满足,求解后返回(3)。
4 算例分析
为了阐明本文方法的有效性和实用性,在计算环境为Core(TM)i3-2330 CPU 2.20GHz 8GB RAM,对偶间隙收敛标准均设为 0.01%条件下,以 IEEE 118节点系统为例进行说明。该系统包含 118个节点,186条支路,54个发电机组和91个负荷,其中,发电机组成本特性数据见附表 1,其他参量见文献[21],所采用的负荷模式如图 2所示,研究周期内的最大负荷设为6 000MW,预安排设备G10、G20、G34、T96检修,有关检修参量见附表2。
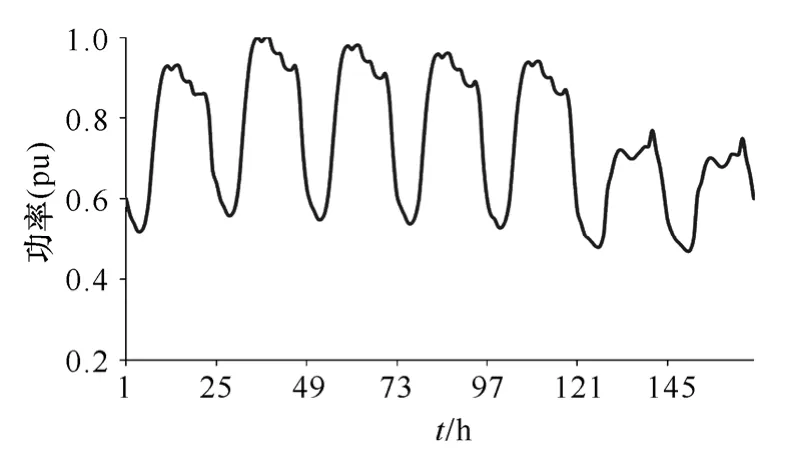
图2 每时段延续1h的负荷需求总模式Fig.2 Load pattern with 1 hour intervals
本算例按三类方法进行决策,第一类按文献[21]仅包含主问题、潮流子问题的 Benders分解方法;第二类为包含主问题、潮流子问题以及辅助问题的Benders分解方法,但不加入潮流子问题集缩减环节;第三类为本文方法。
表1和表2给出了3种方法对应的计算结果,可知:
(1)三种方法决策的检修计划安排及运行成本相同,说明本文算法的有效性。
(2)与方法1相比,方法2增加了7个辅助问题,其中5个辅助问题在低维空间直接对主问题中的输电设备检修计划进行修正,替代了5个高维空间的主问题求解,使解算的主问题数由8个减少为3个,计算时间变为原来的 61.5%,剩余的 2个辅助问题起识别关联机制的作用。当然,计算效率提升程度与主问题模型的复杂度密切相关,主问题模型求解越困难,越能体现辅助问题的重要性。方法3中由于加入了潮流子问题集缩减环节,使待优化的潮流子问题数由1 344个减少为415个,计算总时间变为461 s,仅为方法1的36.8%,由此显现潮流子问题集缩减环节的实用性。
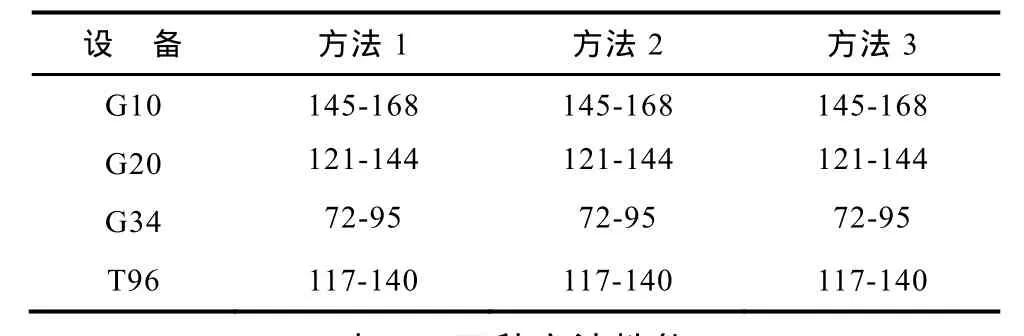
表1 发输电检修计划安排Tab.1 Equipment maintenance schedule
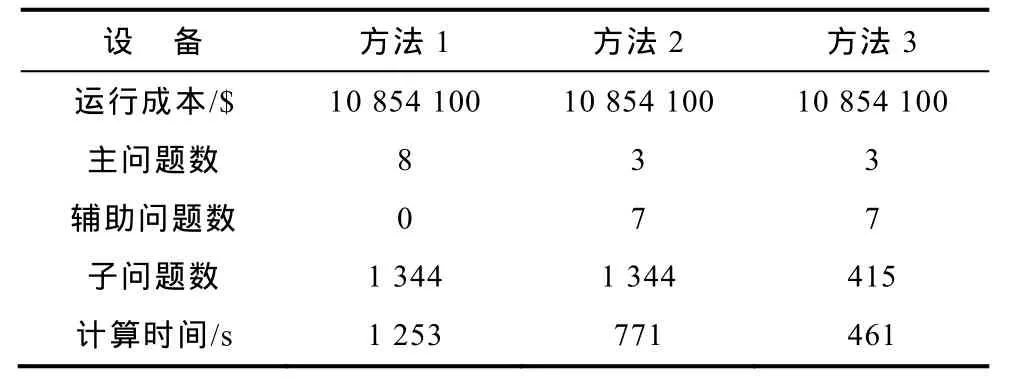
表2 三种方法性能Tab.2 The performance of three methods
5 结论
本文在对设备检修与运行矛盾机理分析基础上提出了发输电检修与机组组合联合决策的 Benders方法,其中,辅助问题的引入以及基于模式识别的潮流子问题集的缩减有效提高了问题的求解效率,对于设备状态检修背景下复杂电网的发输电检修与机组组合联合决策无疑是有价值的。
附 录

附表1 IEEE-118节点系统发电机组成本特性参数App.Tab.1 Generators’ cost data in IEEE-118 bus system
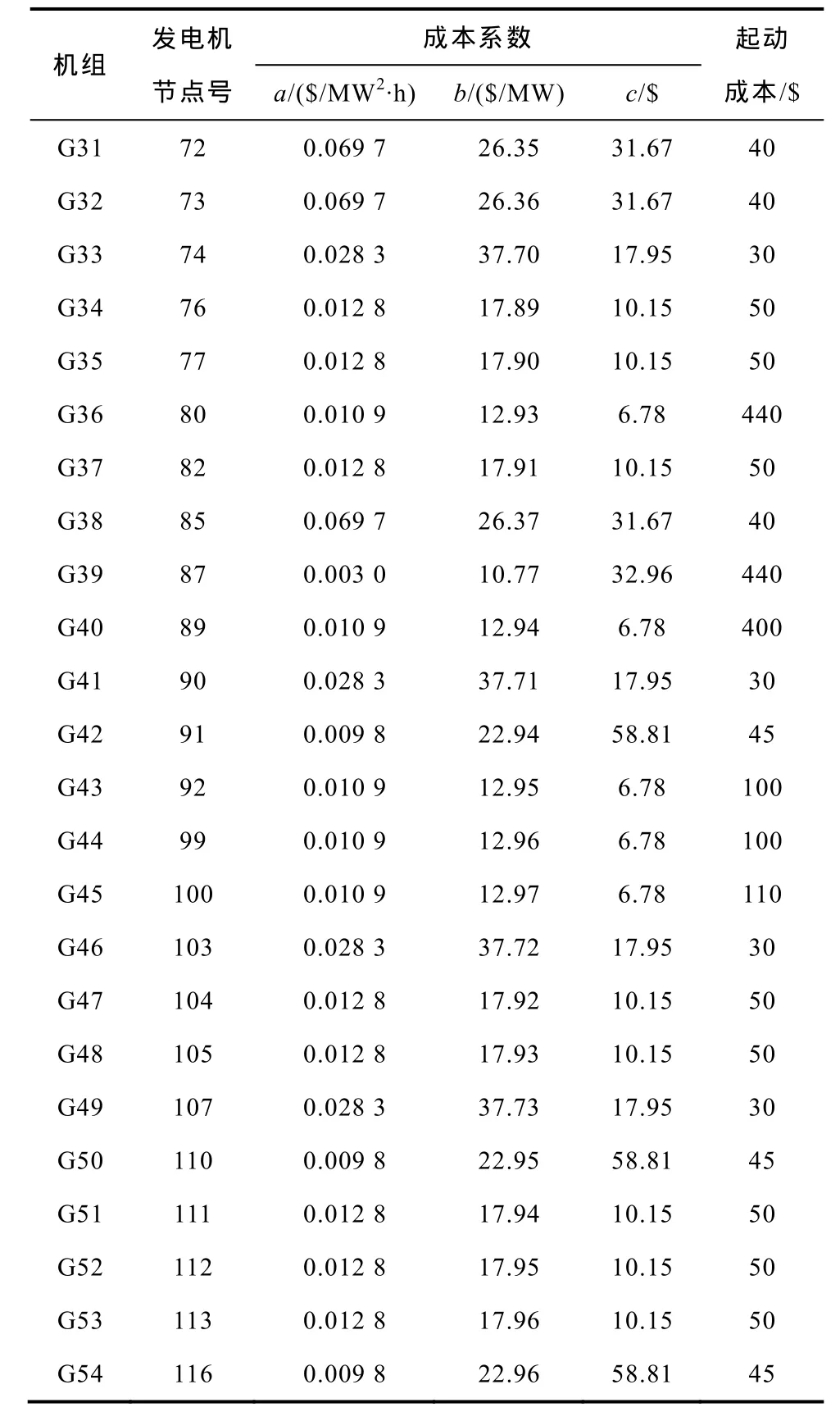
(续)
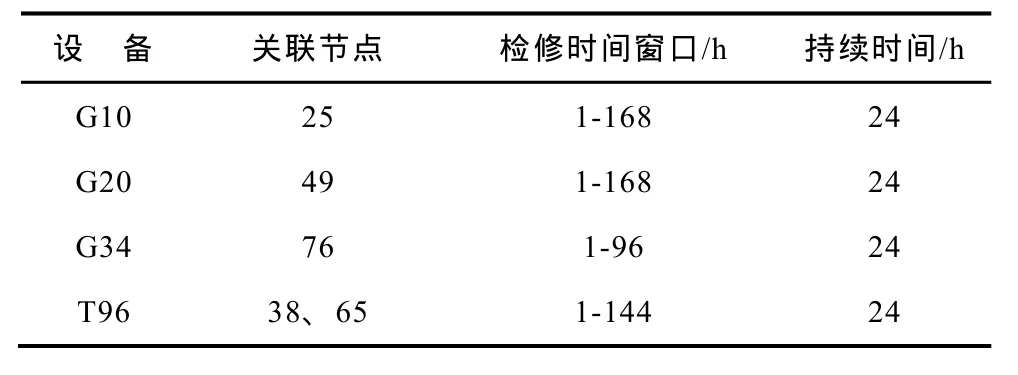
附表2 设备检修参数App.Tab.2 Equipment maintenance data
[1] Shahidehpour M,Marwali M. Maintenance scheduling in restructured power systems[M]. Kluwer Academic Publishers,2000.
[2] Fu Y,Li Z Y,Shahidehpour M,et al. Coordination of midterm outage scheduling with short-term securityconstrained unit commitment[J]. IEEE Transactions on Power Systems,2009,24(4): 1818-1830.
[3] 方陈,夏清,孙欣. 考虑大规模风电接入的发电机组检修计划[J]. 电力系统自动化,2010,34(19):20-24,74.
Fang Chen,Xia Qing,Sun Xin. Generation maintenance scheduling with significant wind power generation[J].Automation of Electric Power Systems,2012,34(19):20-24,74.
[4] 李明,韩学山,杨明,等. 电网状态检修概念与理论基础研究[J]. 中国电机工程学报,2011,31(34): 43-52.
Li Ming,Han Xueshan,Yang Ming,et al. Basic concept and theoretical study of condition-based maintenance for power transmission system[J]. Proceedings of the CSEE,2011,31(34): 43-52.
[5] Wu L,Shahidehpour M,Fu Y. Security-constrained generation and transmission outage scheduling with uncertainties[J]. IEEE Transactions on Power Systems,2010,25(3): 1674-1685.
[6] Christiaanse W R,Palmer A H. A technique for the automated scheduling of the maintenance of generating facilities[J]. IEEE Transactions on Power Apparatus and Systems,1972,91(1): 137-144.
[7] Garver L L. Adjusting maintenance schedules to levelize risk[J]. IEEE Transactions on Power Apparatus and Systems,1972,91(5): 2057-2063.
[8] 魏少岩,徐飞,闵勇. 输电线路检修计划模型[J].电力系统自动化,2006,30(17): 41-49.
Wei Shaoyan,Xu Fei,Min Yong. Modeling on maintenance scheduling of transmission lines[J]. Automation of Electric Power Systems,2006,30(17): 41-49.
[9] 高卫恒,王建学,路建明,等. 基于等风险度的输电系统检修计划[J]. 电力系统自动化,2012,36(7):6-11.
Gao Weiheng,Wang Jianxue,Lu Jianming,et al.Maintenance schedule of transmission system based on equal risk[J]. Automation of Electric Power Systems,2012,36(7): 6-11.
[10] Benders J F. Partitioning procedures for solving mixed-variables programming problems[J]. Numerische Mathematik,1962,4: 238-252.
[11] Chen L,Toyoda J. Optimal generating unit maintenance scheduling for multi-area system with network constraints[J]. IEEE Transactions on Power Systems,1991,6(3): 1168-1174.
[12] Silva E L,Morozowski M,Fonseca L G,et al.Transmission constrained maintenance scheduling of generating units: a stochastic programming approach[J]. IEEE Transactions on Power Systems,1995,10(2): 695-701.
[13] Marwali M K C,Shahidehpour M. Integrated generation and transmission maintenance scheduling with network constraints[J]. IEEE Transactions on Power Systems,1998,13(3): 1063-1068.
[14] Marwali M K C,Shahidehpour M. Long-term transmission and generation maintenance scheduling with network,fuel and emission constraints[J]. IEEE Transactions on Power Systems,1999,14(3): 1160-1165.
[15] Geetha T,Shanti Swarup K. Coordinated preventive maintenance scheduling of GENCO and TRANSCO in restructured power systems[J]. International Journal of Electrical Power and Energy Systems,2009,31(10):626-638.
[16] 丁明,冯永青. 发输电设备联合检修安排模型及算法研究[J]. 中国电机工程学报,2004,24(5): 18-23.
Ding Ming,Feng Yongqing. Research on the modeling and algorithm to global generator and transmission maintenance scheduling[J]. Proceedings of the CSEE,2004,24(5): 18-23.
[17] 于大洋,韩学山,赵建国. 发输电协调检修计划的主从规划模型与分区搜索算法[J]. 电网技术,2010,34(4): 88-93.
Yu Dayang,Han Xueshan,Zhao Jianguo. A bilevel programming model and partition searching algorithm for integrated maintenance schedule[J]. Power System Technology,2010,34(4): 88-93.
[18] da Silva E L,Schilling M Th,Rafael M C. Generation maintenance scheduling considering transmission constraints[J]. IEEE Transactions on Power Systems,2000,15(2): 838-843.
[19] Pandzic H,Conejo A J,Kuzle I,et al. Yearly maintenance scheduling of transmission lines within a market environment[J]. IEEE Transactions on Power Systems,2012,27(1): 407-415.
[20] Marwali M K C,Shahidehpour M. Coordination between long-term and short-term generation scheduling with network constraints[J]. IEEE Transactions on Power Systems,2000,15(3): 1161-1167.
[21] Fu Y,Shahidehpour M,Li Z Y. Security-constrained optimal coordination of generation and transmission maintenance outage scheduling[J]. IEEE Transactions on Power Systems,2007,22(3): 1302-1313.
[22] Ostrowski J,Anjos M,Vathony A. Tight mixed integer linear programming formulations for the unit commitment problem[J]. IEEE Transactions on Power Systems,2012,27(1): 39-46.
[23] Jorge N,Stephen W. Numerical optimization[M]. 2nd ed. New York: Springer,2006.
