无极灯用LCCL谐振变换器特性分析与研究
2015-11-14林国庆
沈 豫 林国庆
(福州大学电气工程与自动化学院 福州 350116)
1 引言
提高开关频率可以减小电感、变压器等磁性元件的体积和重量,提高变换器的功率密度。然而随着开关频率的提高,开关损耗增加,严重影响了电路的工作效率以及开关器件的使用寿命。高频谐振变换器利用其自身的谐振特性,可以实现开关管的零电压开关(Zero Voltage Switching,ZVS)或者零电流开关(Zero Current Switching,ZCS),具有开关损耗小、效率高、EMI小等优点[1,2]。根据负载与谐振电路的连接关系,谐振变换器可以分为串联谐振变换器、并联谐振变换器以及串并联谐振变换器等。通过改变谐振回路的电路结构,可以改善电源性能,实现电源在许多特殊使用场合的特殊要求,满足多种不同性能负载的供电需要[3,4]。因此,高频谐振变换器的应用十分广泛,无极灯电子镇流器则是谐振变换器在照明领域的典型应用[5]。高频谐振变换器的性能好坏与谐振回路结构及其参数的设计是否合理有很大的关系,因此,对这种电路的设计主要围绕谐振回路来进行[6,7]。在众多高频谐振变换器中,LCCL变换器兼有串联和并联谐振变换器各自的优点,但由于具有4个谐振元件,其分析与设计十分复杂。文献[8]中研究的是二阶谐振回路,结构没有多阶谐振回路灵活多样,分析设计也相对简单。文献[9,10]对谐振回路的参数设计都是以基波分析法为基础,但在分析和设计时所采用的固有谐振频率表达式都是假设变换器工作在开路状态得到的,忽略了负载等效电阻的影响,并不符合变换器的实际工作情况;同时,这些设计也没有考虑到实际工作中由于变换器谐振回路参数变化导致电路固有谐振点发生偏移时,开关管是否还能实现ZVS。
本文结合无极灯负载,推导出考虑负载变化时谐振回路固有谐振频率表达式。在此基础上,对高频LCCL变换器谐振回路的阻抗特性和电压增益特性进行了详细分析,得到了各谐振参数对变换器稳态特性的影响,对谐振回路参数进行了设计。同时,考虑到实际工作中变换器固有谐振频率的变化情况,给出了保证开关管实现 ZVS的限定条件以及谐振参数的调整方向。最后,通过实验对所提出的方案进行验证。
2 谐振变换器的电路拓扑及特性分析
2.1 电路拓扑及工作原理
高频LCCL变换器的电路结构如图1a所示,由电压型半桥逆变电路、串并联谐振回路和耦合线圈等组成。电压型半桥逆变电路由开关管Q1和Q2组成,串并联谐振回路由电感Lr、Lc和电容Cr、Cb等组成。耦合线圈由激励电感Lc和无极灯灯管等离子体放电环组成。灯管等离子体放电环和匝数为Nc的激励电感线圈之间可等效成一个耦合系数为k、互感为M的变压器,其中激励电感线圈相当于变压器的一次绕组,等离子体放电环相当于变压器二次侧的单匝绕组[11]。
图1b中是高频LCCL变换器电路的主要工作波形,其中uin表示半桥电路中点电压,ugs1和ugs2分别表示逆变桥上、下开关管的驱动电压,tf表示半桥中点电压uin从Udc下降到0的时间,td表示死区时间,T为开关周期。半桥逆变电路把功率因数校正(Power Factor Correction,PFC)电路输出的直流电压变换成方波信号,再经由谐振回路转换成高频交流信号,供给无极灯负载。

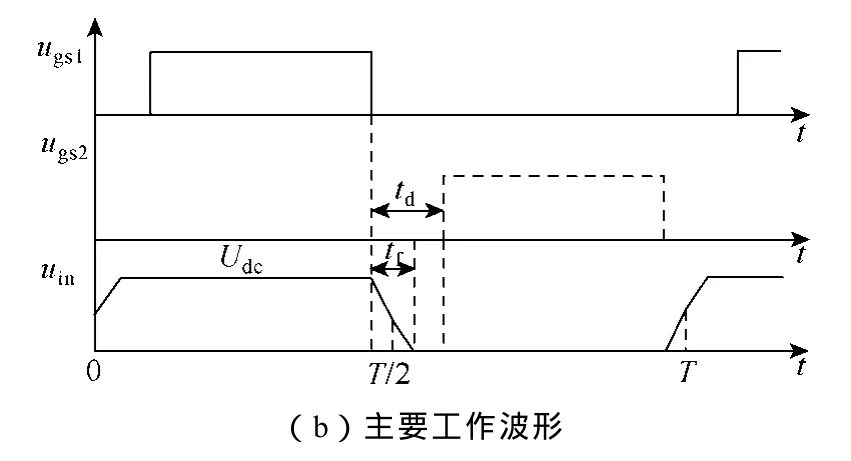
图1 高频LCCL变换器的电路结构及主要工作波形Fig.1 Circuit structure and main operational waveforms of high-frequency LCCL converter
2.2 谐振回路的阻抗特性
高频LCCL变换器工作时,电路中的有效成分都是正弦量,本文采用基波分析法对电路特性进行分析。为分析方便,对电路进行如下假设[12]:
(1)变换器中所有的元件都是理想元件。
(2)开关管Q1和Q2交替导通,谐振回路的输入电压uin是一个占空比为 0.5、幅值等于Udc的方波。
(3)变换器的工作频率f接近谐振回路固有谐振频率f0。
(4)电容Cb远远大于电容Cr。
利用等离子体放电环和激励电感线圈之间的耦合关系,把耦合电感二次侧元件参数映射到耦合电感的一次侧,并进行等效变换,可以得到如图2所示的高频LCCL变换器的等效电路模型。
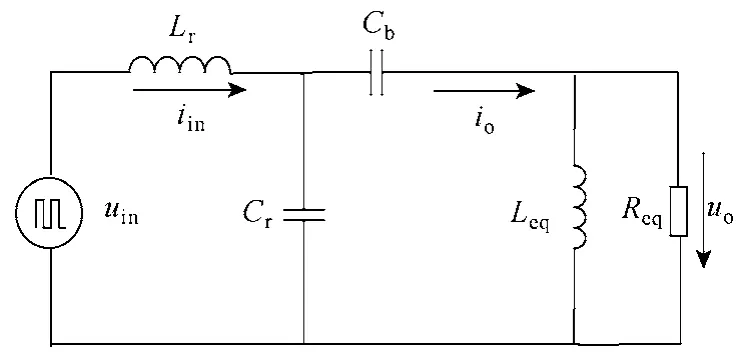
图2 高频LCCL变换器等效电路Fig.2 Equivalent circuit of high-frequency LCCL converter
图 2中,uin和iin分别为谐振回路的输入电压和电流,Lr、Cr分别为谐振电感和谐振电容,Cb为隔直电容,Leq、Req分别为无极灯参数映射到耦合线圈一次侧的等效电感和等效电阻,且Leq≈Lc。
根据图2可以得到谐振电路阻抗为

式中,f为变换器的工作频率。经推导可以得到电路中从低到高的三个固有谐振频率f1、f2和f3,分别为
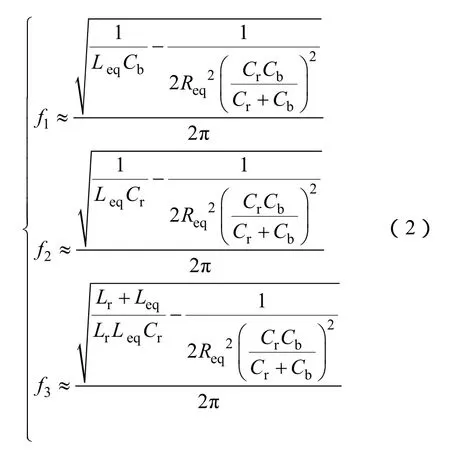
在实际工作中,根据无极灯工作特性,变换器工作频率选择在最高固有谐振频率f3附近。由于Cb>>Cr,为便于分析,最高固有谐振频率f3可用f0表示为,且定义如下电路参数:

由于多阶谐振回路的分析和推导十分复杂,以往对多阶谐振回路的分析大多建立在变换器开路(Req→∞)的基础上[10],其推导的固有谐振频率为。频率f0、f3和f4在不同负载等效电阻Req下的值如图3所示(nc=0.05)。从图3中可以看出,当Req较大时,这三条曲线几乎重合;当Req较小时,f0与f3的曲线几乎重合,而f4与f3的曲线相差较大。

图3 不同电阻Req下,频率f0、f3和f4的曲线Fig.3f0、f3andf4vs.Req
本文分析的电路结构主要应用于无极灯电子镇流器。由无极灯的负载特性可知,启动时灯电阻很大,负载近似于开路;灯点亮时,灯电阻急剧变小。因此,必须考虑负载电阻变化对固有谐振频率的影响。图3中圆点标示位置为本文实验中所采用负载对应的固有谐振频率,此时f0与f4相差7kHz。在固有谐振频率(β=1)附近,谐振回路特性随频率变化较大,如图4和图5所示。因此,在对变换器进行分析和设计时必须要考虑Req的影响。本文选择频率f0对电路进行分析,既相对于f3简化,又相对于f4可以更加准确地反映变换器的特性。

图4 不同负载下的阻抗标幺值曲线Fig.4 Per-unit impedance curves with different loads

图5 谐振回路的电压增益曲线Fig.5 Voltage gain curves of resonant network
选取Z0作为基准值,则输入阻抗的标幺值为
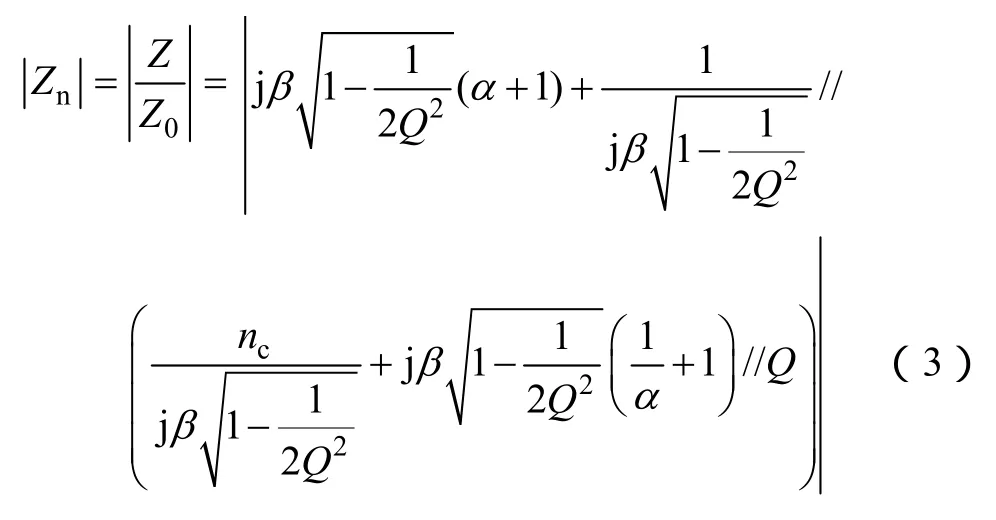
根据式(3)可以得到不同负载下的阻抗标幺值曲线(nc=0.05)如图4所示。可以看出,空载(Q→∞)时曲线有两个极值点βc和βl。当β<βc时,变换器电路工作在容性区域;当β>βl时,变换器电路工作在感性区域;当β介于两者之间时,要根据阻抗角大小来判断电路的工作状态。令式(3)中阻抗标幺值的虚部等于0,可以得到感性区域和容性区域的分界线Q0(α,β,nc)(见图 5b)。当Q>Q0(α,β,nc)时,电路工作在容性状态;当Q<Q0(α,β,nc)时,电路工作在感性状态。
2.3 谐振回路的电压增益特性
假设电容Cb足够大(远大于Cr),在谐振回路中其容抗可以忽略不计,可以推导出谐振回路的电压增益为

式中,Uo是输出电压uo的基波分量有效值;Uin是输入电压uin的基波分量有效值。
下面分两种情况进行讨论:
(1)Q值不变,改变α的取值,得到一族电压增益与频率比值β的曲线,如图5a所示。在每条曲线峰值的左边,增益呈上升趋势,且变化相对较为平缓,即频率的变化对增益的影响相对较小;在峰值右边,增益呈下降趋势,且变化相对较为剧烈,即频率的变化对增益的影响相对较大。同时,α值越大,对于同一β,电压增益越小。也就是说,如果α值较大,电压调节能力较弱,输入电压较小时,有可能达不到所需要的输出电压。当β=1时,图5a中所有曲线同时达到峰值。这也就是说,对于同一个Q值,无论α取值为多少,电压增益Mu均取得最大值,此时工作频率恰好等于频率f0。
(2)α值不变,改变Q的取值,得到一族电压增益与频率比值β的曲线,如图5b所示。可以看出,当Q≥(0.5)1/2时,在β=1处,增益曲线有极大值,为
当Q→∞时,电压增益为。
当Q值取Q0(α,β,nc),电压增益分界线近似为
在βc与βl之间,这条分界线划分了变换器工作状态的容性区域和感性区域。图中阴影部分是容性区域。工作在感性区域是变换器开关管实现ZVS的必要条件。Q值越小,谐振回路的感性区域越大,电路越容易在较大频率变化范围内实现软开关;Q值越大,电压增益的最大值越高,符合无极灯启动时负载电阻很大,并且需要高压启动的特性。
3 谐振回路参数设计
3.1 谐振电感Lr的计算
谐振回路的输入有功功率为
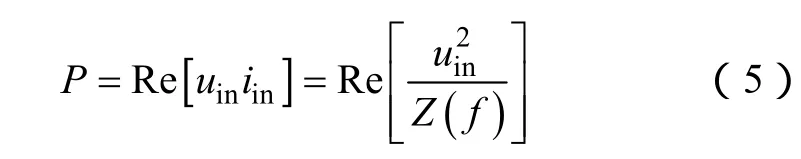
经过推导可以得出当f=f0时,Re[uin2/Z(f)]有最大值,此时谐振回路的输出功率最大,即

令功率比值

式中,Po为变换器实际工作时谐振回路的输出功率。由式(4)和式(7),可得出
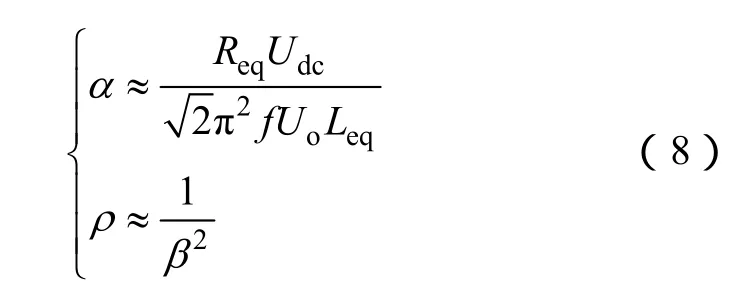
则谐振电感

3.2 谐振电容Cr的计算
为使开关管实现ZVS,必须为开关管的驱动设定合理的死区时间。假设开关管两端的并联电容分别为C1和C2(其中包含开关管的寄生电容),由图1可以得到在电容C2两端的电压uin从Udc下降到0的时间段tf内有

式中,uCb≈Udc/2为电容Cb两端的电压。
解得
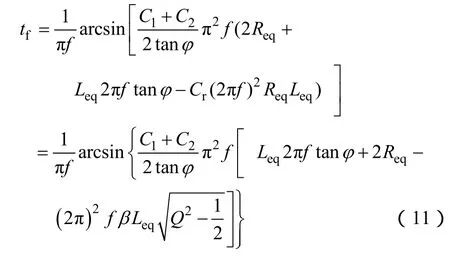
式中,φ是谐振回路输入阻抗的阻抗角。
为了实现开关管的 ZVS,必须满足tf≤td。由此可以得到保证开关管实现 ZVS的最小频率比值βmin。假设变换器固有谐振频率的变化范围是 (f0-Δf,f0+Δf),则与此对应的β范围是。因此,若要保证固有谐振频率偏移后开关管仍可以实现ZVS,必须满足

由式(7)可以看出,ρ越接近于1,谐振回路的输出功率就越接近于最大输出功率。因此,实际参数设计时频率比值β的取值必须兼顾最大功率和式(12)的开关管ZVS条件,分两种情况进行讨论:
(1)若β=1时,,则可取β=1。
(2)若β=1时,,则需重新选择β的取值。

将α和β代入式(7)并进行化简可以得到谐振电容
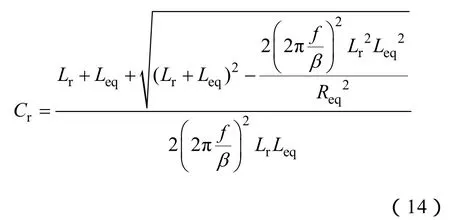
3.3 谐振参数变化对开关管ZVS的影响
由式(11)可以得到图6所示的tf随谐振参数变化的曲线。可以看出,电压下降时间tf的大小与频率比值β、电感Lr和电容Cr的大小成反比,与电容C1(C2)的大小成正比。当频率比值β、电感Lr和电容Cr越大,电容C1(C2)越小时,tf越小,开关管越容易实现ZVS。在图6a、图6b和图6c的参数条件下,使开关管实现ZVS的最小频率比值β、谐振电感Lr和谐振电容Cr分别为 0.89、196μH和2.87nF,图6d参数条件下,使开关管实现ZVS的最大电容C1(C2)为193pF。在电路设计中,可以根据这个规律对参数进行调整,以确保开关管实现ZVS。

图6 下降时间tf与谐振参数的关系Fig.6tfvs. resonant parameters
4 实验结果
基于上述分析,设计了一台85W的无极灯电子镇流器原理样机。主要参数如下:PFC输出直流电压Udc=400V,谐振变换器工作频率f=250kHz,谐振变换器输出电压有效值Uo=200V,等效电感Leq=156μH,死区时间td=280ns,电容Cb=0.1μF。实验结果见图7。
图 7a所示为样机的实测电压增益曲线与理论计算电压增益曲线。可以看出,通过基波分析法得出的理论计算电压增益曲线与实测值基本相符。
图 7b所示为灯启动时,输出电压uo的波形。从图中可以看出,灯启动过程输出电压逐渐增大,当灯点亮时,uo迅速减小到额定电压。
图7c所示为额定工作时,输出电压uo的波形,可见由于变换器工作在固有谐振频率附近,变换器输出电压为正弦波。
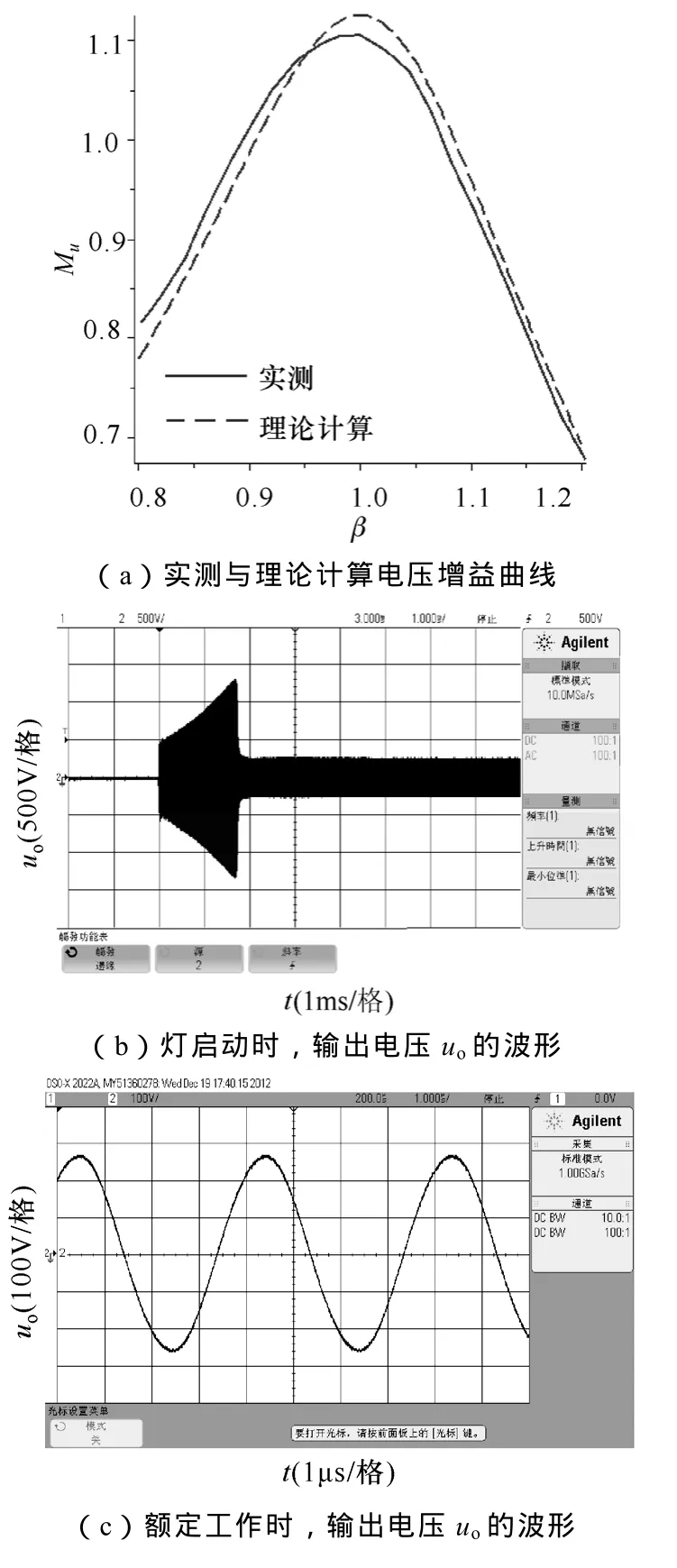
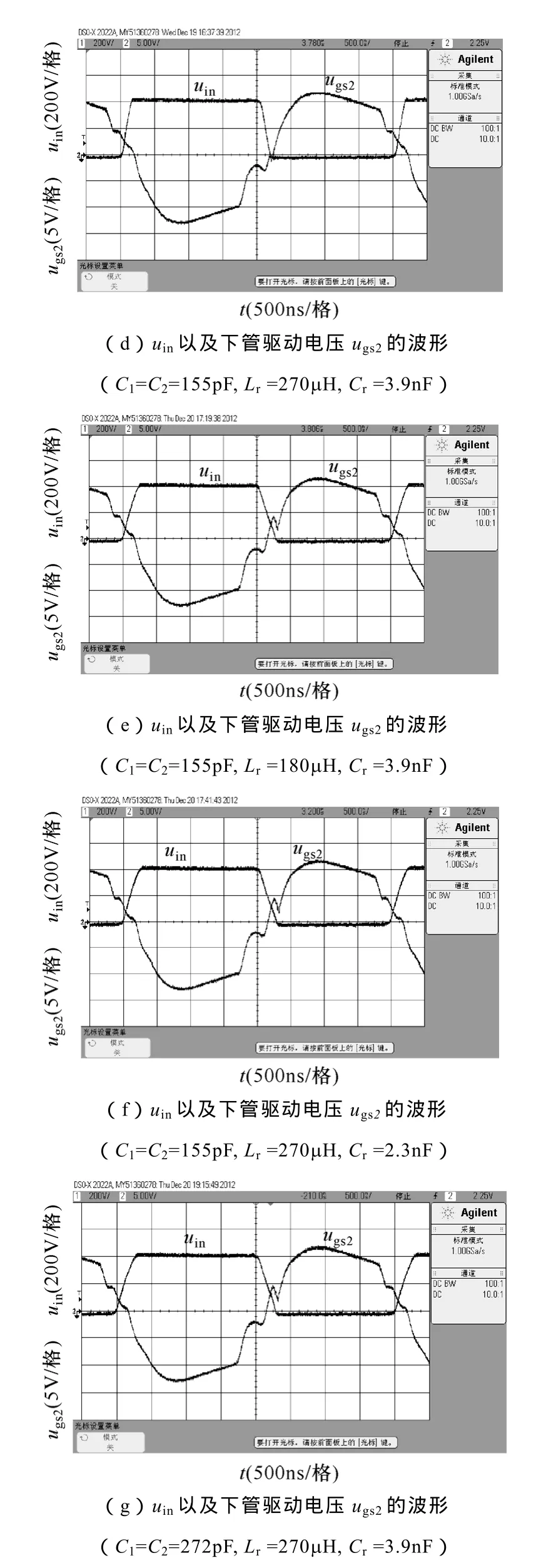
图7 实验结果Fig.7 Experimental results
图 7d~图7g是不同谐振参数下,半桥中点电压uin以及下管驱动电压ugs2的波形。图 7d中电容C1(C2)、谐振电感Lr和谐振电容Cr的取值在图6所要求的软开关范围内,开关管实现了 ZVS;图 7e中电感Lr的取值小于 196μH,图 7f中电容Cr的取值小于 2.87nF,图 7g中电容C1(C2)的取值大于193pF,因此这三种情况下变换器都是硬开关。实验结果与理论分析相一致。
满载时,实测出图7d软开关工作状态下且输出功率最大时变换器的效率为 93%,图 7g硬开关工作状态下变换器的效率为89%。可见,由于变换器实现了最大功率输出,同时开关管实现了ZVS,有效地减少了开关损耗,提高了变换器的工作效率。
5 结论
本文分析了高频LCCL变换器的谐振回路的阻抗特性和电压增益特性,结合无极灯负载,提出一种兼顾最大输出功率和开关管 ZVS的谐振回路参数设计方案。得出以下结论:
(1)根据负载特性,推导出变换器额定工作条件下固有谐振频率的表达式。该表达式考虑了负载变化对固有谐振频率的影响,准确地反映了变换器的实际工作情况。
(2)通过对各个谐振参数对于变换器谐振特性影响的分析,发现当Cb足够大(远大于Cr)时,其对变换器稳态特性的影响比较小;当频率比值β、电感Lr和电容Cr越大,电容C1(C2)越小,开关管越容易实现ZVS。这个规律为变换器谐振回路参数设计方案的调整提供了依据。
(3)提出了一种兼顾最大输出功率和开关管ZVS的参数设计方案,可以保证当电路的固有谐振频率发生适当正负偏差时,开关管仍然能够实现ZVS。
(4)用一台85W无极灯电子镇流器原理样机进行实验,表明采用这种兼顾最大输出功率和开关管 ZVS条件的参数设计方案可以有效地提高变换器的效率,验证了理论和设计方案的准确性以及可行性。
[1] 陈申,吕征宇,姚玮. LLC谐振型软开关直流变压器的研究与实现[J]. 电工技术学报,2012,27(10):163-169.
Chen Shen,Lü Zhengyu,Yao Wei. Research and verification on LLC resonant soft switching DC-DC transformer[J]. Transactions of China Electrotechnical Society,2012,27(10): 163-169.
[2] Chu C L,Li C H,Skibinski G. Analysis and design of a current-fed zero-voltage-switching and zero-currentswitching CL-resonant push-pull DC-DC converter[J].IET Power Electronics,2009,2(4): 456-465.
[3] Tschirhart D J,Jain P K. Design procedure for high-frequency operation of the modified seriesresonant APWM converter to reduce size and circulating current[J]. IEEE Transactions on Power Electronics,2012,27(10): 4181-4191.
[4] Lin C,Chen W. 60 kHz Electronic ballast for electrodeless fluorescent lamp[C]. IEEE Industrial Technology Conference,2009: 1-6.
[5] Jang T,Kim H J,Kim H. Dimming Control Characteristics of Electrodeless Fluorescent Lamps[J]. IEEE Transactions on Industrial Electronics,2009,56(1):93-100.
[6] 王春芳,徐勤超. 变频微波炉电源用LLC谐振变换器[J]. 电工技术学报,2012,27(6): 103-109.
Wang Chunfang,Xu Qinchao. Study of LLC resonant converter for variable-frequence microwave oven power supply[J]. Transactions of China Electrotechnical Society,2012,27(6): 103-109.
[7] Lee I O,Moon G W. Analysis and design of a threelevel LLC series resonant converter for high- and wide-input-voltage applications[J]. IEEE Transactions on Power Electronics,2012,27(6): 2966-2979.
[8] Hwang S H,Jung D Y,Jung Y C,et al. Soft-switching bi-directional DC/DC converter using a LC series resonant circuit[C]. IEEE Electrical Machines and Systems Conference,2011: 1-5.
[9] De Simone S,Adragna C,Spini C. Design guideline for magnetic integration in LLC resonant converters[C]. IEEE Power Electronics,Electrical Drives,Automation and Motion Conference,2008: 950-957.
[10] 张智娟. 高频感应加热电压型逆变器功率控制研究[D]. 保定: 华北电力大学,2010.
[11] Cao X H. Design orientated model and application of electronic ballasts for two toroidal ferrite coupled electrodeless lamps[C]. IEEE Applied Power Electronics Conference,2005: 1764-1769.
[12] 张卫平. 开关变换器的建模与控制[M]. 北京: 中国电力出版社,2006.
