基于改进的广义谐波小波包分解和混沌振子的小电流接地系统故障选线
2015-11-14张淑清师荣艳姜万录
张淑清 马 跃 李 盼 师荣艳 姜万录 董 璇
(燕山大学电气工程学院 河北省测试计量技术及仪器重点实验室 秦皇岛 066004)
1 引言
我国在中低压配电网中大多数采用中性点不接地方式和中性点经消弧线圈接地方式,二者均为小电流接地方式,当发生系统单相接地故障时依然可以正常工作 1~2h。但长时间带故障运行,可能会使故障发展为相间短路、三相短路及故障设备烧毁等严重后果,破坏系统安全运行。因此,及时且准确地选出故障线路对防止故障进一步扩大,保证系统正常供电非常重要[1-3]。
目前故障选线方法大致分为基于故障稳态特征的方法[4]和基于故障暂态特征的方法[5-9]。基于故障稳态特征的方法主要是利用基波零序电流的大小和方向构成选线判据。然而中性点经消弧线圈接地系统发生单相接地故障后,由于消弧线圈的补偿作用,故障线路与非故障线路基波零序电流的方向有可能相同,且非故障线路基波零序电流幅值有可能大于故障线路,因此,利用基波零序电流进行选线不容易实现。而零序电流的暂态分量,无论在何种接地方式下,健全线路暂态零序电流的大小与本线路对地电容的大小成正比,而故障线路零序电流暂态分量等于所有健全线路暂态零序电流之和,且方向相反,不存在稳态零序电流中由于得到消弧线圈感性电流的补偿作用故障线路的稳态零序电流可能出现倒相的问题,因此可用其实现选线[10,11]。
基于故障暂态特征的方法关键问题是如何实现信号的特征提取。常用的信号特征提取方法有小波分解、小波包分解和谐波小波包分解等[12-15]。小波分析在信号分析中占据相当重要的地位,是针对信号的全程频率进行分解,得到感兴趣的频段,但分析效果受小波基函数影响较大,也不能完全还原混合信号的特征;谐波小波函数具有互相垂直的偶函数与奇函数,构成零相移滤波器,不提供任何附加相位。然而,广义谐波小波分解与小波分析一样具有二进分解的特点,分析结果不能任意选取感兴趣的频段,没有更好的适应性。
Duffing振子微弱信号检测方法是一种有效的弱信号检测方法[16-18],它不受噪声影响且对于与内驱动力同频的外界信号具有高度敏感性,当微弱的周期信号出现时,系统会立即发生相变,根据系统的相变便可以将微弱的周期信号检测出来。Duffing振子在小频率参数条件下有良好的检测效果,而在频率过大时难以实现预期效果。然而,在电力系统实际应用中检测信号很多为大频率信号,也就无法使用 Duffing振子系统进行检测。因此,需要对Duffing振子系统进行尺度变换,或称为时标变换,以适应不同频率信号的检测要求。
本文在原有的广义谐波小波包分解方法[19,20]基础上,对其频率适应性进行改进,消除了频段及分解层次的限制,实现任意起始频率、分解层数及分析范围的分解。利用改进的广义谐波小波包算法对各线路零序电流进行分解可以提取各线路暂态信息最集中的特征频段。
将时标变换法应用到 Duffing振子系统中,克服了 Duffing振子系统的小频率参数限制。将故障电流信号分解后,选出的特征频带作为外驱动力输入到经时标变换的振子系统中,利用混沌振子相图变化正确选出故障线路。对不同故障点和接地相进行了仿真验证,理论分析及实验结果证明了该方法的优势和有效性。
2 广义谐波小波包分解的改进算法
设由实部和虚部组合而成的复函数F(ω)为f(t)的傅里叶变换
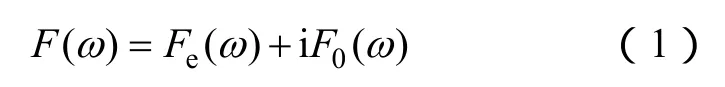
式中,Fe(ω)和F0(ω)分别为与2π有关的偶函数和奇函数,表达式分别为

对F(ω)进行傅里叶逆变换得函数f(t)
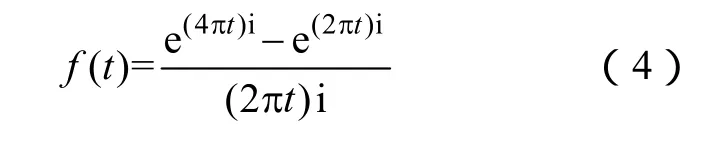
式(4)即为谐波小波函数。
为使频带选取更灵活,引入a、b(a<b)∈R+,则频带变为ω∈[2πa,2πb],则
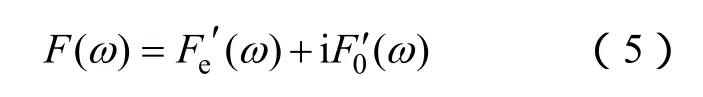
相应的偶函数和奇函数为

对F(ω)进行傅里叶逆变换,可得到小波函数


式(9)即为频带宽为2π(b-a),分析频带中心为k(b-a)的广义谐波小波的一般形式。
对上式进行离散化,设离散信号为u(t),t=0,1,2,…,N-1,则u(t)的广义谐波小波变换的离散形式[21]为

可以看出,对信号f(t)作谐波小波分解,可以将信号既无交叠又无遗漏地分解到相互独立的频段,任何能量较弱的细节信号都可以被准确地显现出来。然而二进的谐波小波分析的结果不能任意选取感兴趣的分析频段,在实际应用中,有时需要对信号的低频、高频部分都同等对待,为此,采用二进小波包的分解思想来实现自适应任意细化的谐波小波包分解。令分析频带各子带带宽和每级尺度分析频带的上、下限频率a、b分别为

式中,fs为采样频率;j为分解层数。
得到广义谐波小波包变换的离散形式为

因此,随着分解层数j的逐渐增大,就可以应用谐波小波包对信号的整个频带进行无限细分。
谐波小波包保持了谐波小波的零相移滤波特性,且实现了对信号的无限细分,然而它是对整个频带进行分析,在工程应用中,很多时候只需要对某一特定频段进行分析,若利用广义谐波小波包进行分析,无疑增大了计算量。因此,重新设置起始频率和频带带宽。
设待分析频段为f1~f2,其中f1为起始频率,f2为终止频率(f1<fs2,f2<fs2)。则待分析频带宽度 Δf( Δf+f1≤fs2)为

将起始频率f1加入到每级尺度分析频带的上、下限频率a、b中,则式(12)变为

为使算法更加灵活,将信号分解到任意频率宽度,引入分解层数k(k为大于1的整数)。各子带带宽B变化为

将式(14)~式(16)代入到式(13)中即可得到改进的谐波小波包变换的离散形式。
可以看到,通过对谐波小波包算法进行改进,在应用中可以根据实际情况选择需要的频段进行分析,可以自由设置起始频率和终止频率,并且消除了对分解层数的限制,可以将信号分解到任意频率宽度。
3 混沌振子检测原理及算法
Duffing振子微弱信号检测方法是一种有效的微弱信号检测方法。本文采用 Holmes型 Duffing振子检测系统,该系统对噪声具有一定的免疫力,而且当微弱的周期信号出现时,系统会立即发生相变,根据系统的相变便可以将微弱的周期信号检测出来[17,18,22]。
Holmes型Duffing方程的基本形式为
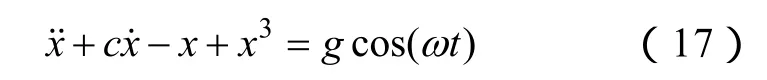
其动力学方程表示为
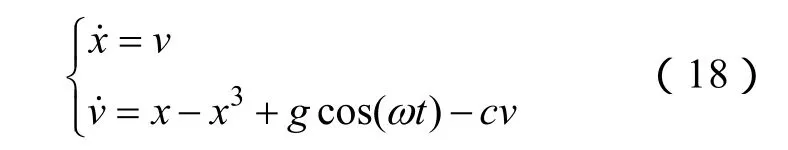
式中,c为阻尼比;x(或x(t))为状态变量,随时间t变化;-x+x3为非线性恢复力;gcos(ωt)为周期策动力,并且一般对Holmes型Duffing方程进行研究时取ω=1。
在没有外部被测信号干扰的情况下,将阻尼比c固定,令周期策动力g从0开始逐渐增大,其系统的状态将逐渐发生变化。当g较小时,相轨迹表现为Poincare映射下的吸引子,相点在(±1,0)两焦点附近作周期振动。当g超过一定阈值时,将出现同宿轨道,随着g的增大,出现倍周期分岔,紧接着进入混沌状态,这一过程随着g的变化非常迅速。在此过程中,g在很大一段范围内都会使系统处于混沌状态,此时存在一个阈值gd,当g增大到gd时,系统处于由混沌转为周期运动的临界状态;当g大于gd时,系统进入大尺度周期运动状态。
固定c值,调节g值至gd使系统处于由混沌转为周期运动的临界状态。加入同频率的待检测信号z(t)=λcos(t+φ)得如下形式

式中,λ为待测信号幅值;φ为待测信号与内驱动信号的相位差。
化为动力学方程为

对式(20)进行整理,得系统总策动力为
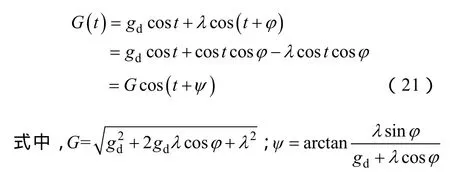
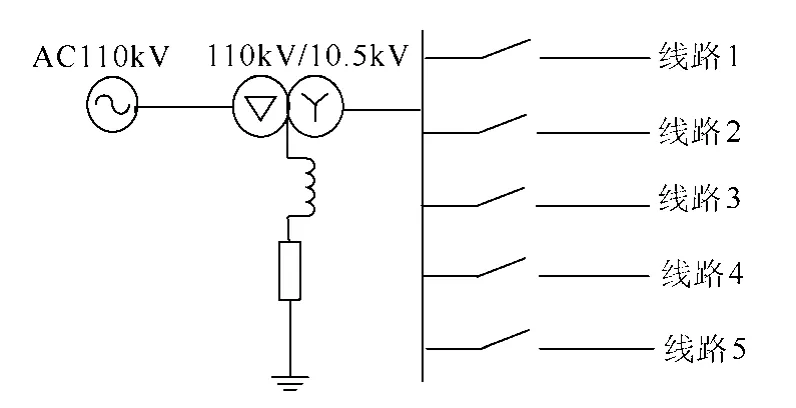
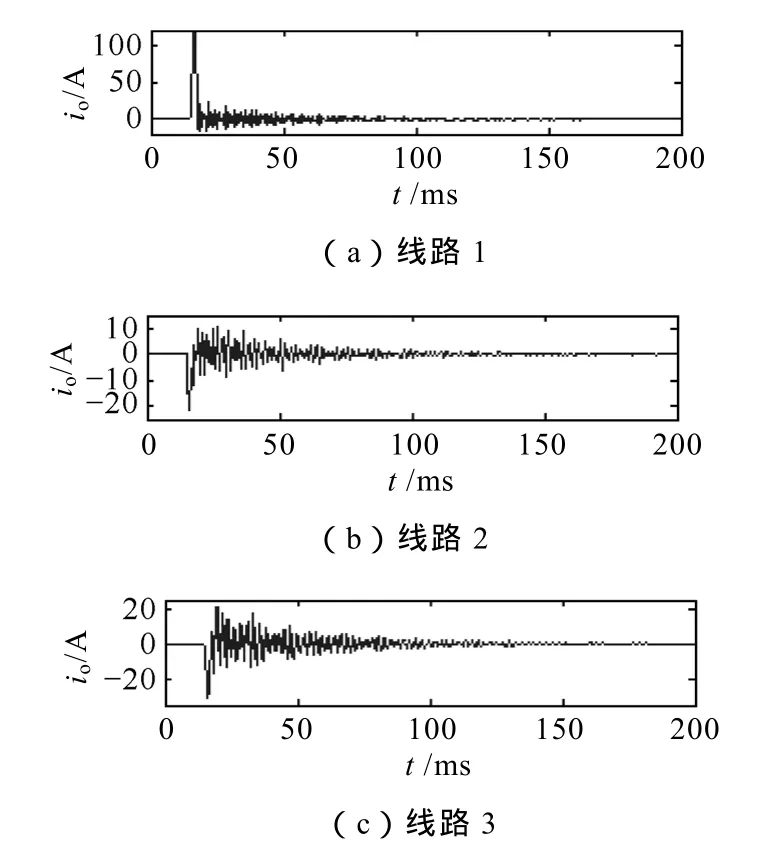
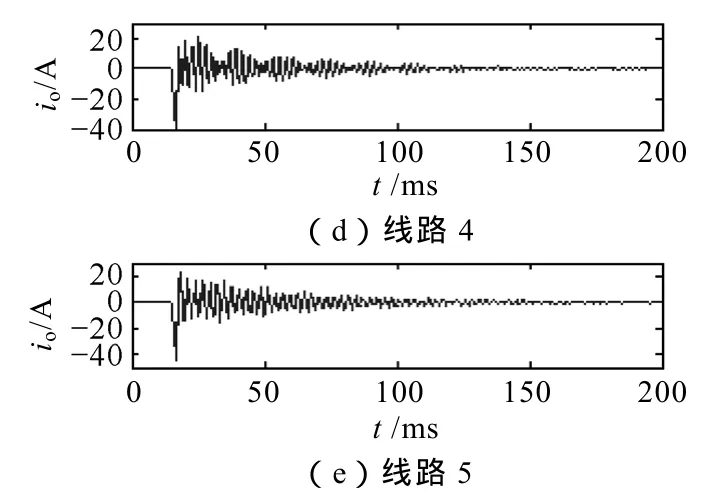
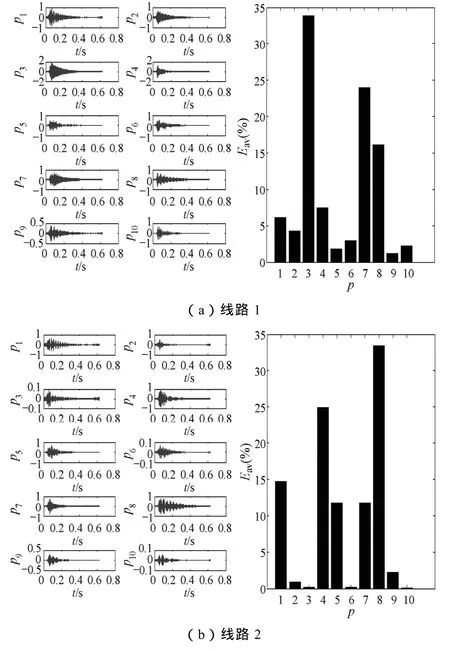
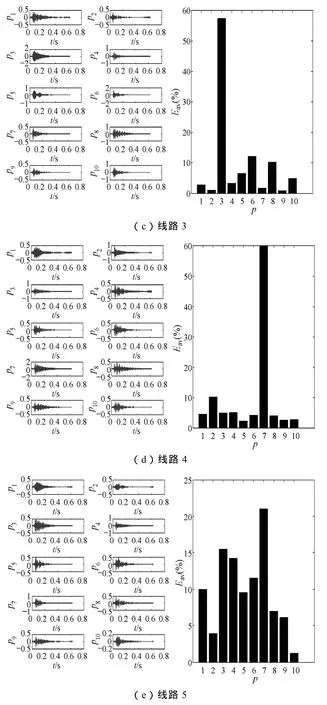
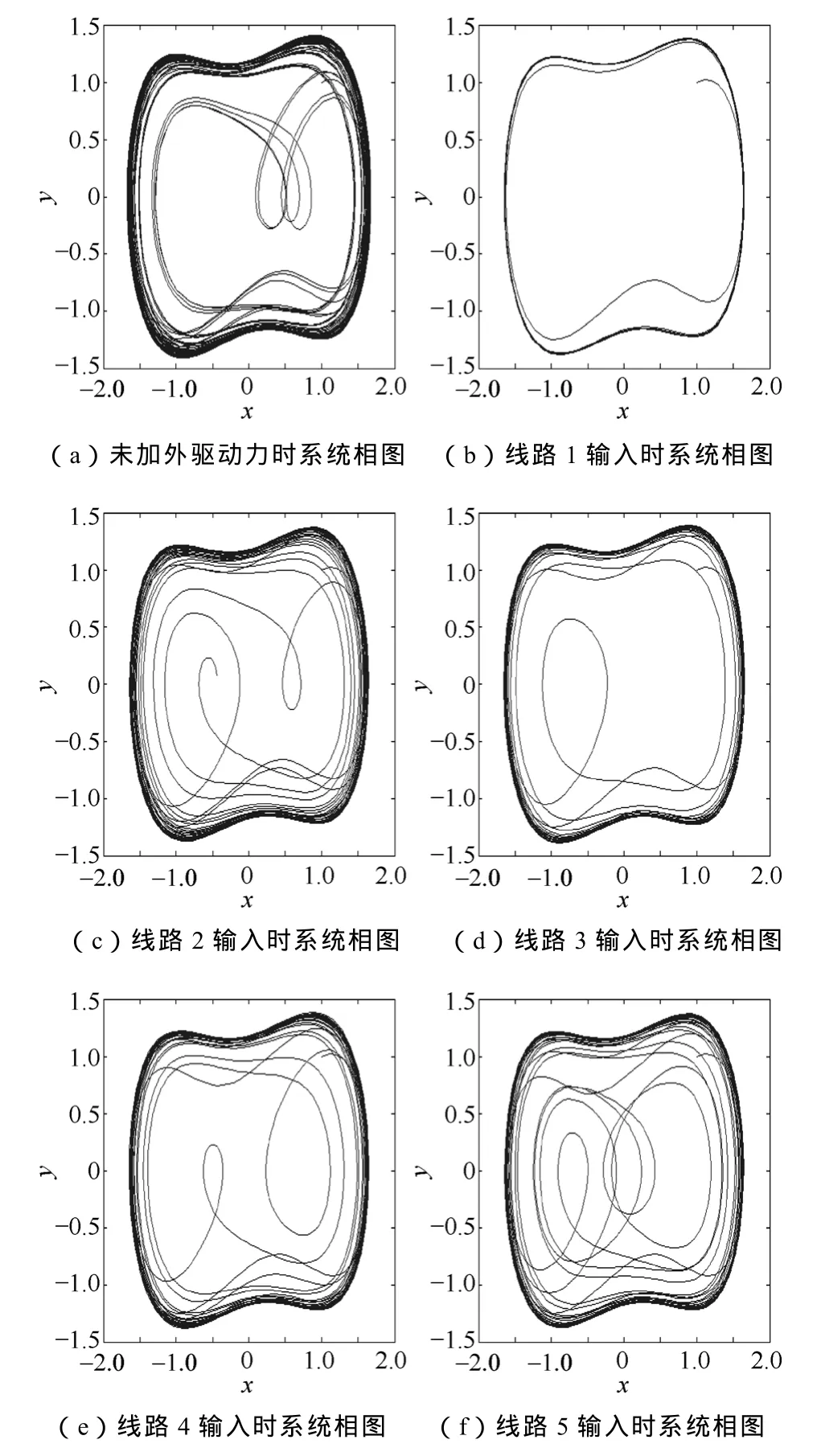
当λ< 时,G≤gd,系统仍处于混沌状态,不会产生到大周期状态的相变;当φ不符合上述关系时,G>gd,此时系统会出现从混沌状态到大周期状态的相变。据此可以判别待检测信号的相位关系。 以上研究均是在ω=1的情况下进行的,而实际应用中待检测频率是多种多样的,当内驱动信号角频率不为1时,即将t用ω0t代替,经整理得到式(20)的变化形式为 对比式(23)和式(20)可以看出,x˙和v˙都变成了原来的ω0倍,在相平面上表现为相点在每一时刻的速度为以前的ω0倍,而系统的其他性质,例如系统的分岔值,丝毫没有发生变化。 经大量仿真实验研究发现,驱动力频率过大会严重影响系统动态响应性能,即难以出现混沌状态到大周期状态的变化,也就是说 Duffing振子在小频率参数条件下有良好的检测效果,而在过大频率时难以实现预期效果[23]。然而,在实际应用中检测信号很多为大频率信号,也就无法使用 Duffing振子系统进行检测。因此,需要对 Duffing振子系统进行尺度变换,或称为时标变换,以适应不同频率信号的检测要求。 时标变换即对被测信号进行时间尺度上的扩展,使角频率为ω0=2πf0的待检测信号与ω=1rad/s建立等价关系。 对于待检测信号z(t)=λcos(ω0t+φ),令t' =ω0t,则z(t')=λcos(t' +φ),即将t在时间轴上放大ω0倍, 相当于将角频率ω0在频率轴上压缩到了ω=1rad/s。 时标的扩展是通过调节算法步长实现的。设信号的采样频率为fs,那么在角频率为ω0的外界信号一周内的采样点数为n=fsf0,在n和f0之间必须满足关系 因此,在ω=1rad/s对应的一个周期内,Runge-Kutta法运算n步对应的步长为 因此,可以通过调节算法步长对待测信号进行时标扩展,使ω0≠1rad/s的待测信号与ω=1rad/s相匹配,进而应用前文所述的相位检测方法对系统进行检测。当待测信号相位满足式(22)时,系统处于混沌状态;否则,系统将会出现从混沌状态到大周期状态的相变。 调节周期策动力g值至gd。将提取出的特征频段乘以相应的检测因子输入到 Duffing振子中作为系统的外驱动力,采用龙格库塔法(Runge-Kutta)对方程求解获得系统的相图,利用计算机自动识别系统是混沌状态还是周期状态。 当小电流接地系统发生单相接地故障,无论在何种接地方式下,故障线路零序电流暂态分量等于所有非故障线路暂态零序电流之和,且极性相反;母线故障时,所有线路的暂态零序电流的极性都相同。因此如果某条线路使系统发生相变(保持混沌状态),而其余线路仍使系统保持混沌状态(使系统发生相变),则可判定使系统发生相变(保持混沌状态)线路为故障线路。 用ATP仿真软件进行仿真分析,建立中性点经消弧线圈接地系统仿真模型,仿真模型如图1所示。 图1 输电线路仿真模型Fig.1 The simulation model of transmission line 仿真模型中每个元件的参数以及系统设置如下: 采用110kV交流电源。变压器采用三角形-星形-星形联结。消弧线圈采用过补偿方式,补偿度取8%,串联电阻取消弧线圈感抗的 10%。线路 1~5的长度依次为:20、25、30、35、40km。 线路正序参数:R1=0.6Ω/km;L1=1.25mH/km;C1=9.48×10-3μF/km。 线路零序参数:R0=0.2Ω/km;L0=5.51mH/km;C0=5.9×10-2μF/km。 设置采样频率为 3 200Hz,仿真时间 0.2s,设置故障发生在线路 1的 60%处,故障发生时间为0.015s。各线路的零序电流如图2所示。 图2 发生故障后各线路零序电流Fig.2 Zero-sequence current in each line after fault 暂态电容电流的自由振荡频率一般在 300~1 500Hz,且为了避免工频及单次谐波的影响,本文对500~1 500Hz频段进行分析,利用改进的广义谐波小波包算法进行分解,提取暂态高频分量。 对各线路的零序电流进行改进的广义谐波小波包分解,选定起始频率f0=500Hz,频宽Δf=1 000Hz,k=10,则各个分量的频率范围分别为500~600Hz,600~700Hz,700~800Hz,800~900Hz,900~1 000Hz,1 000~1 100Hz,1 100~1 200Hz,1 200~1 300Hz,1 300~1 400Hz,1 400~1 500Hz。5 条线路零序电流经改进的广义谐波小波包分解后分量及各层系数的能量条形图如图3所示。 图3 5条线路零序电流分解后分量及各层系数能量条形图Fig.3 The components and the factor bar charts of each layer decomposed from 5 line zero-sequence currents 图3中,左方各图分别为线路1~线路5零序电流经改进的广义谐波小波包分解后的各个分量,右方各图分别为线路1~线路5分解后各层系数的能量条形图。 从图3中可以看出,各线路暂态高频分量所在频带均不一样,线路1~5的暂态高频分量所集中的频带依次为:p3、p8、p3、p7、p7。求取系数p3、p7、p8的频谱范围分别为:700~800Hz、1 100~1 200Hz、1 200~1 300Hz。 在未加入待测信号前,设置 Duffing振子系统的阻尼比c=0.5,内驱动力gd=0.826。 将各线路提取出的特征频带分别输入混沌振子中,检测因子经试验调试设定为0.000 5。混沌振子驱动力角频率分别为ω1=1 500π、ω2=2 500π、ω3=1 500π、ω4=2 300π、ω5=2 300π。进行时标变换为角频率ω1=1rad/s时,步长分别为h1=1.473s、h2=2.454s、h3=1.473s、h4=2.258s、h5=2.258s;时标变换前后的变换倍数k1=1/(1 500π)、k2=1/(2 500π)、k3=1/(1 500π)、k4=1/(2 300π)、k5=1/(2 300π)。实验结果如图4所示。 图4 各线路特征频带输入混沌阵子系统后系统相图Fig.4 Duffing oscillator system’s phase diagram when adding each line’s signal 图4中,图4a为混沌系统中未加入待检测信号的相图,整个系统完全由内驱动力驱动,系统状态为明显的混沌状态。图4b~图4f分别为线路1~5提取的特征频带输入到混沌振子后系统的相图变化,可以看出,线路1出现了明显的相变,从混沌状态转入到大周期运动状态,而线路 2、3、4、5仍然都处于混沌状态,因此判定线路1为故障线路,与仿真设置是一致的。 对不同故障点和接地相进行仿真验证,结果见下表所示。从表中可以看出,本文提出的选线方法对不同情况下的故障均能准确做出判断,未出现错选或漏选,进一步验证了该方法的有效性。 实际的工程装置中,高压电流互感器感应的电流信号可以由DSP或FPGA系统采集及预处理。为了能让编程人员在 PC上方便地观察实验运行过程中数据处理结果,以及在实验中通过PC对DSP或FPGA 中内部数据进行修改,应用串行通信完成数据的传输,可以在PC上方便地观察实验运行过程,提高编程的效率。通信软件有计算机超级终端、Visual Basic、Visual C以及组态软件等。 改进的广义谐波小波包分解不仅继承了谐波小波零相移滤波特性和谐波小波包的能够对信号的无限细分的特性,而且消除了对起始频率、带宽和分解层数的限制,实现了更加简便和精细的信号分解。将时标变换方法应用到混沌振子中,克服了Duffing振子对大频率信号的限制,实现了对任意频率成分信号的检测。当配电网发生单相接地故障时产生不对称的零序电流,利用改进的广义谐波小波包算法对各线路零序电流进行分解提取各线路暂态信息最集中的特征频段,确定起始频率、频宽及分层数。利用混沌振子相图变化正确选出故障线路。对不同故障点和接地相进行了仿真验证,理论分析及实验结果证明了该方法的有效性。 [1] 贾清泉,石磊磊,王宁,等. 基于证据理论和信息熵的消弧线圈接地电网融合选线方法[J]. 电工技术学报,2012,27(6): 191-197. Jia Qingquan,Shi Leilei,Wang Ning,et al. A fusion method for ground fault line detection in compensated power networks based on evidence theory and information entropy[J]. Transactions of China Electrotechnical Society,2012,27(6): 191-197. [2] 张钧,何正友,贾勇. 基于 S变换的故障选线新方法[J]. 中国电机工程学报,2011,31(10): 109-115. Zhang Jun,He Zhengyou,Jia Yong. Fault line identification approach based on s-transform[J]. Proceedings of the CSEE,2011,31(10): 109-115. [3] Liu J H,Liang R,Wang C L,et al. Application of fractal theory in detecting low current faults of power distribution system in coal mines[J]. Mining Science and Technology,2009,19(3): 321-325. [4] 林湘宁,高艳,刘沛,等. 基于零序补偿导纳的小电流接地系统单相故障保护新方法[J]. 中国电机工程学报,2006,26(10): 45-49. Lin Xiangning,Gao Yan,Liu Pei,et al. A novel method to identify the single phase-to-earth fault in the neutral un-effectual grounded system using the zero-sequence compensated admittance[J]. Proceedings of the CSEE,2006,26(10): 45-49. [5] 董新洲,毕见广. 配电线路暂态行波的分析和接地选线研究[J]. 中国电机工程学报,2005,25(4): 1-6. Dong Xinzhou,Bi Janguang. Analysis on transient traveling wave and study on fault line selection for distribution lines[J]. Proceedings of the CSEE,2005,25(4): 1-6. [6] 束洪春,彭仕欣,李斌,等. 基于零序电流激励的谐振接地系统故障选线测后模拟方法[J]. 电工技术学报,2008,23(10): 106-113. Shu Hongchun,Peng Shixin,Li Bin,et al. Simulation after detecting fault line in resonant earthed system through zero sequence current motivation[J]. Transac-tions of China Electrotechnical Society,2008,23(10):106-113. [7] 郭谋发,刘世丹,杨耿杰,等. 利用时频谱相似度识别的配电线路接地选线方法[J]. 中国电机工程学报,2013,33(19): 1-9. Guo Moufa,Liu Shidan,Yang Gengjie,et al. A novel approach to detect fault line in distribution network using similarity recognition based on time-frequency spectrum[J]. Proceedings of the CSEE,2013,33(19):1-9. [8] 李斌,束洪春. 基于瞬时实功率和瞬时虚功率的谐振接地系统单相接地选线新方法[J]. 电工技术学报,2012,27(6): 183-190. Li Bin,Shu Hongchun. A new integration method of fault line detection in resonant earthed system based on instantaneous real power and instantaneous virtual power[J]. Transactions of China Electrotechnical Society,2012,27(6): 183-190. [9] 肖先勇,张文海,汪颖,等. 基于故障相暂态信号特征的二维故障选线法[J]. 电网技术,2012,36(5):178-184. Xiao Xianyong,Zhang Wenhai,Wang Ying,et al. Twodimensional fault line detection based on transient signal features of fault phase[J]. Power System Technology,2012,36(5): 178-184. [10] Lin Xiangning,Ke Shuohao,Gao Yan,et al. A selective single-phase-to-ground fault protection for neutral uneffectively grounded systems[J]. International Journal of Electrical Power & Energy Systems,2011,33(4): 1012-1017. [11] 张钧. 配电网智能故障诊断与谐波源定位研究[D].成都: 西南交通大学,2012. [12] He Z,Cai Y,Qian Q. A study of wavelet entropy theory and its application in power system[C]. Proceedings of IEEE Conference on Intelligent Mechatronics and Automation,Chengdu,China,2004: 847-851. [13] Catalao J P S,Pousinho H M I,Mendes V M F.Hybrid wavelet-PSO-ANFIS approach for short-term electricity prices forecasting[J]. IEEE Transactions on Power Systems,2011,26(1): 137-144. [14] 赵元喜,胥永刚,高立新,等. 基于谐波小波包与BP审计网络的滚动轴承声发射模式识别技术[J].振动与冲击,2010,29(10): 162-165. Zhao Yuanxi,Xu Yonggang,Gao Lixin,et a1. Fault pattern recognition technique for roller bearing acoustic emission based on harmonic wavelet packet and BP neural network[J]. Journal of Vibration and Shock,2010,29(10): 162-165. [15] 李明爱,马建勇,杨金福. 基于小波包和熵准则的最优频段提取方法[J]. 仪器仪表学报,2012,33(8):1721-1728. Li Aiming,Ma Janyong,Yang Jinfu. Optimal frequency band extraction method based on wavelet packet and entropy criterion[J]. Chinese Journal of Scientific Instrument,2012,33(8): 1721-1728. [16] Wang G,He S. A quantitative study on detection and estimation of weak signals by using chaotic Duffing oscillators[J]. IEEE Transactions on Circuits and Systems I,2003,50(7): 945-953. [17] 尚秋峰,尹成群,李士林,等. 基于 Duffing振子的微弱正弦信号检测方法研究[J]. 中国电机工程学报,2005,25(2): 66-70. Shang Qiufeng,Yin Chengqun,Li Shilin,et a1. Study on detection of weak sinusoidal signal by using duffing oscillator[J]. Proceedings of the CSEE,2005,25(2):66-70. [18] Shen L,Wang P,Liu W,et al. The application of Melnikov function in weak signal detection with Duffing oscillators[C]. Proceedings of IEEE Conference on Intelligent Control and Information Processing,Harbin,China,2011: 854-858. [19] 张文斌,周晓军,林勇,等. 基于谐波小波包方法的旋转机械故障信号提取[J]. 振动与冲击,2009,28(3): 87-89. Zhang Wenbin,Zhou Xiaojun,Lin Yong,et al.Harmonic wavelet package method used to extract fault signal of a rotation machinery[J]. Journal of Vibration and Shock,2009,28(3): 87-89. [20] 李舜酩. 谐波小波包方法及其对转子亚频轴心轨迹的提取[J]. 机械工程学报,2004,40(9): 133-137. Li Shunming. Harmonic wavelet packets method and used on accurate obtaining the orbit of rotor subfrequency signal[J]. Chinese Journal of Mechanical Engineering,2004,40(9): 133-137. [21] 王玉田,张淑清,董璇,等. 一种改进的广义谐波小波包分解算法及在信号特征提取中的应用[J]. 燕山大学学报,2013,37(4): 358-365. Wang Yutian,Zhang Shuqing,Dong Xuan,et a1.An improved generalized harmonic wavelet packet algorithm and its application in signal feature extraction[J]. Journal of Yanshan University,2013,37(4):358-365. [22] 姜万录,张淑清,王益群. 基于混沌和小波的故障信息诊断[M]. 北京: 国防工业出版社,2005. [23] 赖志慧,冷永刚,孙建桥,等. 基于 Duffing振子的变尺度微弱特征信号检测方法研究[J]. 物理学报,2012,61(5): 60-68. Lai Zhihui,Leng Yonggang,Sun Jianqiao,et a1.Weak characteristic signal detection based on scale transformation of Duffing oscillator[J]. Acta Phys.Sin,2012,61(5): 60-68.

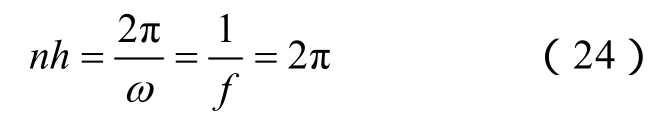
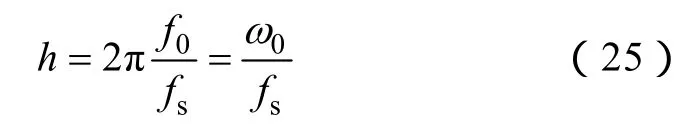
4 选线方法验证
5 结论
