基于标准化结构熵的电网结构对连锁故障的影响
2015-11-14曹一家谭玉东
蔡 晔 曹一家 谭玉东 李 勇
(1. 湖南大学电气与信息工程学院 长沙 410082 2. 国网湖南省电力公司经济技术研究院 长沙 410004)
1 引言
电力网络是覆盖面积最广、结构最复杂的人造系统之一。近年来,国内外电网大停电事故频发[1-3],而大规模停电事故往往是由电网中某个节点或者某几条输电线路发生故障退出运行而引起的。有研究从网络拓扑结构出发,发现网架结构是影响电网动力学特性的关键因素[4,5]。因此,研究电网拓扑结构与故障传播特性之间的关系,对提高电网可靠性,减小大停电概率有着重要的意义。
为研究连锁故障传播机制,复杂网络中的“自组织临界性”和“小世界模型”得到广泛应用。其中,研究复杂网络模型分析元件故障在全网中的传播和演化是研究的热点。连锁故障是一个动态现象且传播速度极快,大停电事故发生概率受幂律支配[6,7]。通常从电网拓扑组织结构和潮流再分配两个方面研究连锁故障对电网的影响。文献[8]通过对中美典型电网的拓扑结构进行比较并定性地分析了小世界网络特性对连锁故障传播的影响,研究表明大部分电力网络属于小世界网络,并认为小世界网络较小的平均距离和较高聚类系数等性质,对故障的传播起到了推波助澜的作用,因此考虑通过改变电网的组织结构缓解故障前期的累积效应,可从源头上抑制连锁故障的传播。文献[9-11]从电气耦合角度出发,引入具有电力系统特征的物理参数,对电力系统复杂网络模型加以改进,从更符合系统实际角度描述了电网的小世界特性与无标度特性。文献[12-16]提出基于不同运行状态的电网脆弱性指标,指出了连锁大停电与电网脆弱性之间的联系。文献[17]研究了节点介数同其容量的关系,同时指出,大量低介数节点即使在介数容量低下时发生故障也很难引起连锁反应,而少数高介数节点在容量很充裕时发生失效也会引发连锁故障。因此除全面提高元件的介数容量外,针对高介数元件,改善网络本身的结构对抑制连锁故障更有实际意义。文献[18]进一步假设节点介数越限时并不马上退出运行,而是通过增大与其相连线路的阻抗,从而迫使一些最短路径绕开该节点以抑制连锁故障的进一步发展。文献[19]提出电气介数概念,研究不同电气介数节点故障对系统连通性和输电能力的影响,同时提出基于生成介数的连锁故障积极防御方法。以上文献虽然较好地从各自角度描述了连锁故障的传播特性,但并未综合考虑电网结构特点与潮流分布两个方面因素定量研究电网固有脆弱性与其动力学行为之间的关系。同时,提出的连锁故障抑制措施与电力系统实际有一定差距,因此有待改进。文献[20,21]在无权网络模型上考虑节点的度分布定义了结构熵概念,建立了简单的无标度网络结构熵模型。文献[22]考虑电力系统电气特性建立新的结构熵模型并将其应用于连锁故障传播特性分析,但是忽略了电网运行方式变化对结构熵的影响,所得结果不能准确反应电力系统实时状态。
针对现有研究的不足,本文首先建立以输电线路电抗值为权重的加权电网拓扑结构模型,定义综合考虑节点和边差异性的结构熵概念。该概念综合考虑电网结构特征和实际电力系统的物理特征,更加符合电力系统实际。其次,利用遗传算法迭代计算相同结构下电网结构熵指标的最大值与最小值,将连锁故障过程中任意时刻结构熵值归一化从而消去电网规模对结构熵指标的影响,得到标准化结构熵值,并将其应用于描述连锁故障过程中电网拓扑结构与输电能力变化,同时辨识电网结构中的“异构”线路。再次,在连锁故障发展过程中,通过主动移除“异构”线路抑制连锁故障蔓延,减小大停电事故严重程度。然后,以IEEE 118节点系统为例,依照相对标准结构熵指标和损失负荷变化建立“异构”线路集,研究在连锁故障发展初期通过主动移除电力系统异构线路来抑制大停电事故。最后,将基于异构线路的连锁故障积极防御策略应用于华北电网,仿真实验结果证明了本文所提方法的有效性。
2 考虑节点和线路差异性的结构熵
在拓扑结构模型中,电网可以用一个加权无向的稀疏连通图G=(V,L,W)描述。V={v1,v2,…,vm}为节点集,代表发电机、变电站和负荷节点,L={l1,l2,…,lm}代表输电线路集合,W={Wl1,Wl2,…,Wlm}为各条线路权重的集合,其中Wl=Xl,Xl为线路l电抗值[22],从而将元件的电气参数特征融入复杂网络模型,更符合电力系统实际。
熵作为描述复杂系统结构的物理量,可以表示物体所处状态是否稳定及系统变化的方向。系统能量分布越均匀,其熵越大;反之,则熵越小。结构熵通过描述节点的差异性定量地分析网络的结构分布特性。如果网络中各个节点的重要度大致相同,则认为网络是“无序”的,相反,节点重要度存在差异则网络是“有序”的。网络结构熵减小,则表明网络由“无序”状态过渡至“有序”状态[23-25]。
考虑到熵是对网络拓扑结构特性度量的宏观指标,而要建立适合电力系统的结构熵指标,必须综合考虑节点和边的差异性,考虑实际系统中节点的物理特征,如:电压等级、功率流向等。电网中能量从发电机节点流向负荷节点,某个节点的度分布值较大则该节点很可能是关键的重要节点。即采用节点度分布概率P(ki)能简单清晰地对网络中节点进行分类,大致描述节点重要度之间的差异性,定义节点i的差异性Si
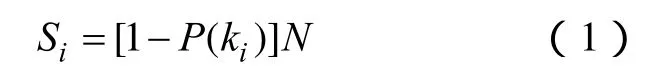
式中,ki表示节点i的度;N为网络的节点数;P(ki)表示节点度为ki的概率。
由电网自身物理特性可知,电网中某个节点的注入功率受与其连接线路和线路阻抗值的影响。节点连接一条边时,认为一个度值为ki的节点被选中的概率应为度值为1的节点的ki倍[20],因此可以选取节点i邻域内的线路权值和∑Wij与ki从节点局部特征描述节点重要度之间的差异性Di如下

综合考虑节点和线路在网络中的差异性,定义中间量iI'和节点i在网络中的重要度Ii
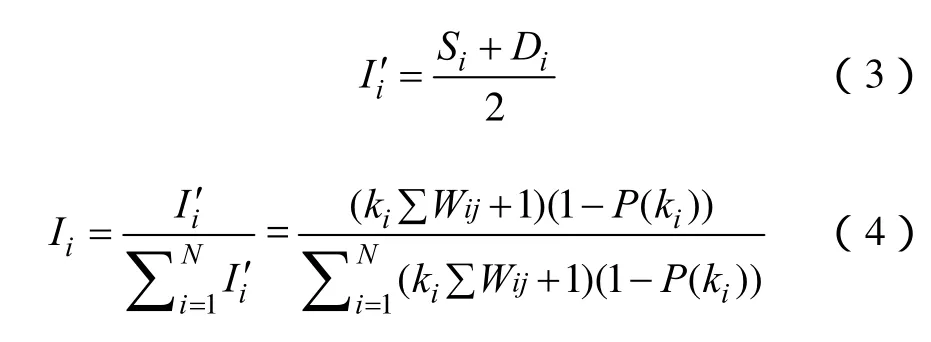
因此,电网的动态结构熵可定义为

式中,N(t)是指t时刻网络中存在的节点数目。
3 加权网络标准化结构熵
3.1 标准化结构熵基本模型
网络结构熵越大则网络越均匀,反之网络结构熵越小网络越不均匀[20-22]。由式(5)可以看出,当电网规模相同时,不同运行方式下,节点的差异性不同,从而会使得电网结构熵随之变化,结构熵指标能很好地描述网络的“有序”情况。但是,由于受到各种因素(隐性故障、人为因素、环境条件等)的影响,电网中某些线路或者节点被切除,电网结构和规模发生变化,使得不同时刻结构熵变化受到网络规模的影响而不能完全评估此时电网组织结构的状态。因此,为消除电网规模对结构熵的影响,需要对结构熵进行标准化。
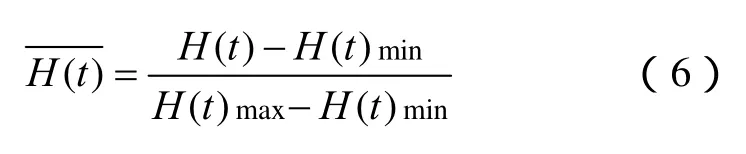
由式(5)可知,某一时刻结构熵大小由线路权值序列{Wij}决定。本文采用遗传算法求得任意时刻电网结构熵的最大值和最小值。以求某时刻电网结构熵的最大值为例,t时刻,W*ijt,k为第k代群种中最优解时线路权值序列,此时按结构熵式(5)计算得到的Ht.k为第k代种群中的最大值。为加速得到t时刻电网结构熵最大值,假设第k-1代群种取得最优解线路权值序列中的最大值和最小值分别为和,并认为第k代群种中的线路权值,ijtkW与和的关系为

以 IEEE 118节点系统为例,求初始时刻电网结构熵最大值与最小值。由图1可以看出,通过大约80代遗传,结构熵最大值Hmax=4.482 876;结构熵最小值Hmin=4.230 821。

图1 IEEE 118节点系统结构熵Fig.1 Structure entropy of IEEE 118-node system
3.2 电网连锁故障模式搜索流程
为研究电力系统连锁故障内在机理,本文引入损失负荷百分比指标 Loss和相对标准结构熵指标评估不同线路退出运行对电网的稳定运行带来的不同影响。
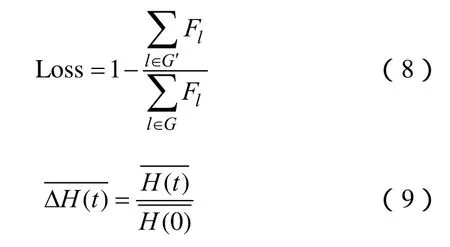
式(8)中,G指故障前网络拓扑图;G'指一次故障后网络拓扑中最大连通图;Fl是指网络拓扑中线路潮流。式(9)中为任意时刻电网的标准化结构熵。
损失负荷百分比的大小可以有效地衡量系统发生故障后不同时刻的电能传输能力,相对标准结构熵指标衡量不同时刻网络拓扑分布的情况。因此,从网络拓扑结构方面综合考虑这两个指标变化,可以评估任意时刻电网组织结构特性对连锁故障的影响。根据上述内容,本文确立电网连锁故障模式搜索流程如下:
(1)参照文献[15]设定模型基本参数。计算线路的直流潮流Fl,设定网络的平均负载率u,线路初始运行容量Lij、最大运行容量Lmax和极限容量Smax。
(2)电网扩容。按照文献[15]的方法,设定仿真实验基本参数,求得故障前系统各线路的最大运行容量、极限运行容量和系统的标准化结构熵,设t=1。
(3)线路按承载潮流大小排序,移除系统初始故障线路。
(4)故障线路承载负荷按照邻域内线路权值重新分配。故障线路上的潮流Fij可按式(10)在邻域内线路之间进行择优分配
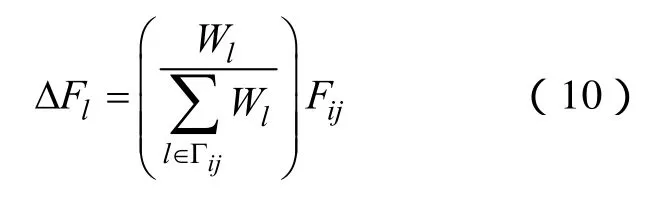
式中,Fij指故障线路ij的潮流;ΔFl指故障线路ij邻域内线路l所分配的负荷;Wl为线路l的权值;为故障线路ij邻域内所有线路权值和。
(5)若潮流重新分配后有输电线路负荷超过其最大运行容量,则过负荷输电线路将由其后备保护的过负荷保护按概率隔离开来,断开概率P(l)如式(11)所示,转入(4)。若各条线路的负荷均未超过其阈值,则连锁故障终止,计算t时刻系统的相对标准结构熵、系统损失负荷比Loss

(6)令t=t+1,转入(3)。
3.3 基于标准化结构熵的电网异构线路识别
不同运行方式下,电网组织结构中某类线路加剧了网络的不均匀性,移除这类线路会使得网架结构变得“均匀”,称这类线路为“异构”线路。相对标准结构熵指标的变化反映了线路对全网组织结构的影响和带给其邻域内线路的“压力”大小。相对标准结构熵越大,说明此时网络的分布越均匀。换句话说,该时刻被移除的线路是使得电网组织结构异构的关键因素。因此,本文根据电网“异构”线路搜索流程对IEEE 118节点系统进行仿真分析。通过比较分析连锁故障过程中任意t时刻相对标准结构熵、系统损失负荷比 Loss建立IEEE 118节点系统最“异构”线路集。选取t时刻相对标准结构熵>1时的故障线路建立“异构”线路集合L1;统计“异构”线路集合 L1中每条线路出现的频次,按照降序排列,选取排名前30%的线路建立“异构”线路集合L2;分别移除“异构”线路集合 L2中每条线路,比较系统发生连锁故障后损失负荷比 Loss,选取 Loss<0.1的线路建立最“异构”线路集合L3。按照上述方法,可以得到IEEE 118节点系统组织结构中最“异构”的线路共30条,见下表所示。
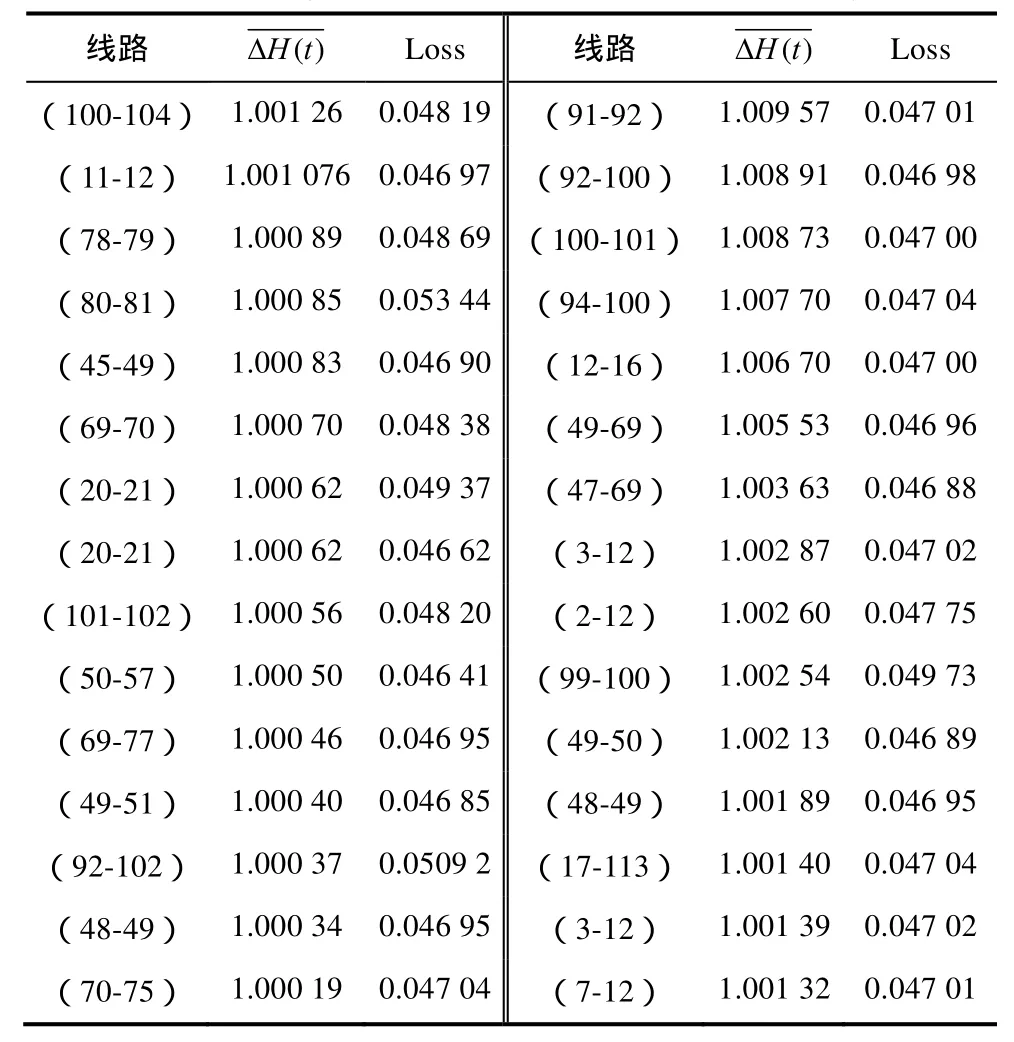
表 IEEE 118节点系统“异构”线路集合Tab. Heterogeneous lines in IEEE 118-node system
4 基于异构线路集的连锁故障积极防御
根据上节内容,电网“异构”线路一般具有以下特点:①“异构”线路本身在系统运行中只承担较小的功率传输,因而移除此类线路不会给系统带来很大的潮流转移;②“异构”线路的介数较小,即此类线路不是系统拓扑结构中的重要联络线,由其连接的节点在整个网络中不属于关键节点;③“异构”线路的移除反而会降低此类线路所在区域的异构性,从而优化了电网组织结构,达到了增强网络鲁棒性的作用。
式(9)中,任意t时刻移除某些线路系统相对标准结构熵越大说明此类线路的存在增加了网络组织结构异构性,使得系统潮流分布不均衡,大停电风险增大。
电网连锁大停电事故的发生与电网本身结构脆弱性密切相关。因此,当电网发生连锁故障时,考虑采取主动切除网络中“异构”线路是一种基于全系统安全角度考虑的具有预防性的行为,可以有效改善电网拓扑结构的脆弱性,降低电网结构的异构性,优化故障后潮流的重新分配,从而避免连锁故障的进一步蔓延。基于标准结构熵的连锁故障积极防御策略具体流程如图2所示。

图2 连锁故障防御流程Fig.2 Defense to cascading failure in power system
但是,系统在某些情况下不宜采取积极防御策略,否则反而会损失大量负荷或者导致系统潮流分布更不均衡,增加大停电事故发生的概率。本文认为以下两种情况下不需要采取防御措施:①t=1时刻,现代电网执行“N-1”安全准则,初始故障后电网仍然满足稳定运行的条件;②系统中运行的“异构”线路大于30%时,主动移除线路过多反而会加重系统的故障程度和失负荷比例。
5 算例分析
5.1 电网相对标准结构熵分布
本文采用Python-2.6.5对IEEE 118节点系统进行仿真建模。当系统负载率分别取u=0.5、0.67和0.83时,统计系统发生200次随机故障时系统的相对标准结构熵和损失负荷,研究电网组织结构特性及其对连锁故障的影响。
图3为IEEE 118节点系统相对标准结构熵累积概率分布图(中间小图为累积概率分布曲线尾部放大图),由图3可以得出未采取防御措施时,较大负载率情况下,电网相对标准结构熵的累积概率较小,系统结构异构性较强。降低系统的负载率可以改善系统的这一情况。这是因为,系统在负载率较高时,初始故障引发的潮流重新分配进一步增大了网络的异构性,从而使得网络的标准结构熵变得更小。未采取防御措施的三条曲线尾部基本重合且标准结构熵最大值大于网络初始结构熵,这说明,电力网络组织结构的异构性是其固有特征,通过降低负载率并不能从根本上提高电网抵抗大停电的能力。采取防御措施后,电力网络的相对标准结构熵明显增大,系统的负载率越低,标准化结构熵的累积概率越高。当系统有较大的备用容量和线路运行裕度时,组织结构的异构性对连锁故障的蔓延起着主导作用。因此,主动移除“异构”线路改善了电力网络的结构不均衡性,能有效抵御大停电事故。
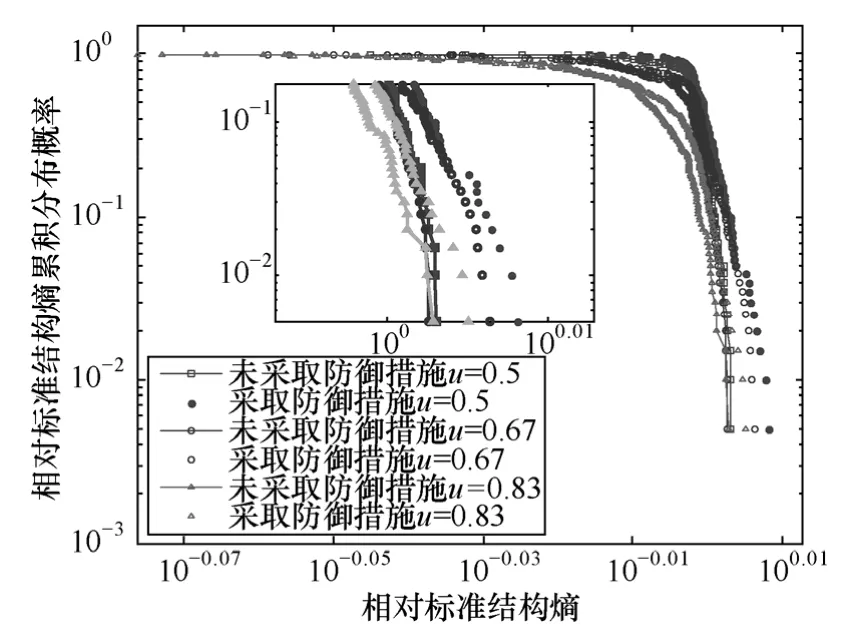
图3 IEEE 118节点系统相对标准结构熵累积概率分布Fig.3 Accumulated probability distribution of standard structure entropy in IEEE 118-node system
5.2 电网自组织临界性分析
由图4中IEEE 118节点系统在不同负载率情况下采取防御策略与未采取防御策略的损失负荷对比分析可以得出:电力网络会随着负载率的升高而进入自组织临界态,随机故障便会触发大停电事故。但电网在平均负载率较低时由于线路潮流分布的高度不均衡性同样可能进入自组织临界态[26],这种情况下可以主动移除网络中的“异构”线路,有效改善故障后潮流的重新分配,虽然主动切除了部分传输线路,但缓解了网络中某些重要线路的“压力”,降低了组织结构的脆弱性,从而增强了网络的鲁棒性。但当系统的负载率很高时,由于线路负荷接近其最大运行容量,因此电网组织结构的改善也阻止不了线路的相继过载而跳开。实际中应确保电力网络运行在一个较高的安全裕度范围。
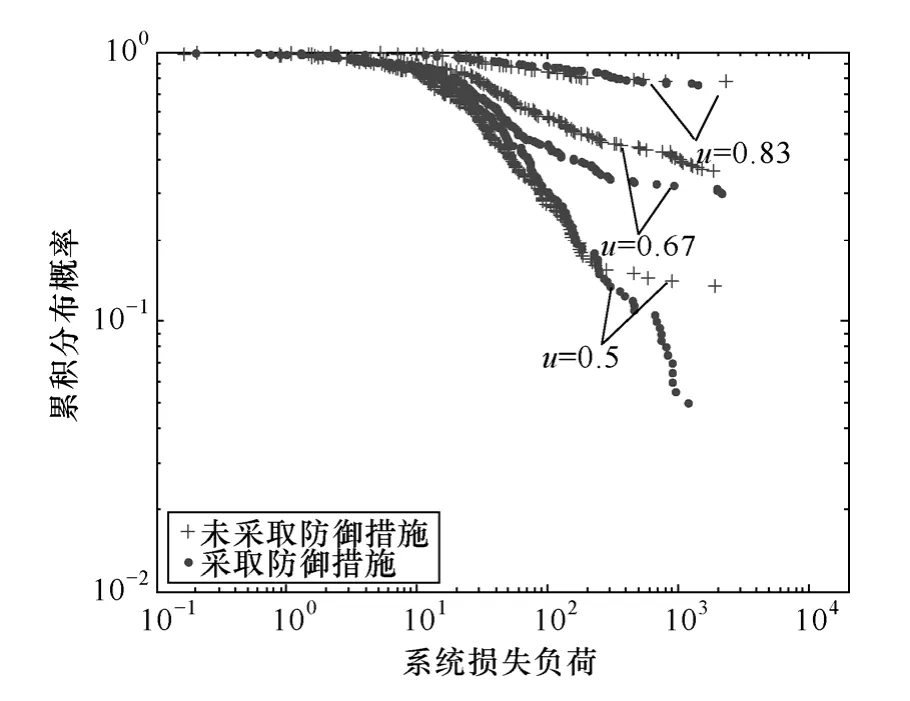
图4 IEEE 118节点系统损失负荷累积概率分布Fig.4 Accumulated probability distribution of power loss in IEEE 118-node system
5.3 华北电网仿真
为验证基于标准化结构熵的电网连锁故障积极防御措施的有效性,在华北电网拓扑结构模型基础上进行仿真计算。华北电网共有 1 621个节点和1 785条支路。按照上节方法,建立华北电网“异构”线路集合,其中共有192条线路。
本文通过随机移除线路触发连锁故障,在连锁故障过程中主动移除3条“异构”线路改善电网组织结构。由仿真结果可知,当系统传输裕度较大时,通过“移除”造成系统异构的关键输电线路,可以改善电网的拓扑组织结构、优化系统故障后潮流的重新分布,从而减小大停电事故的风险。图5分别是华北电网负载率分别为0.2、0.4、0.5、0.67时,系统的损失负荷累积分布图。由图5可以看出,主动移除电网中的“异构”线路能有效减小大停电事故发生的概率。
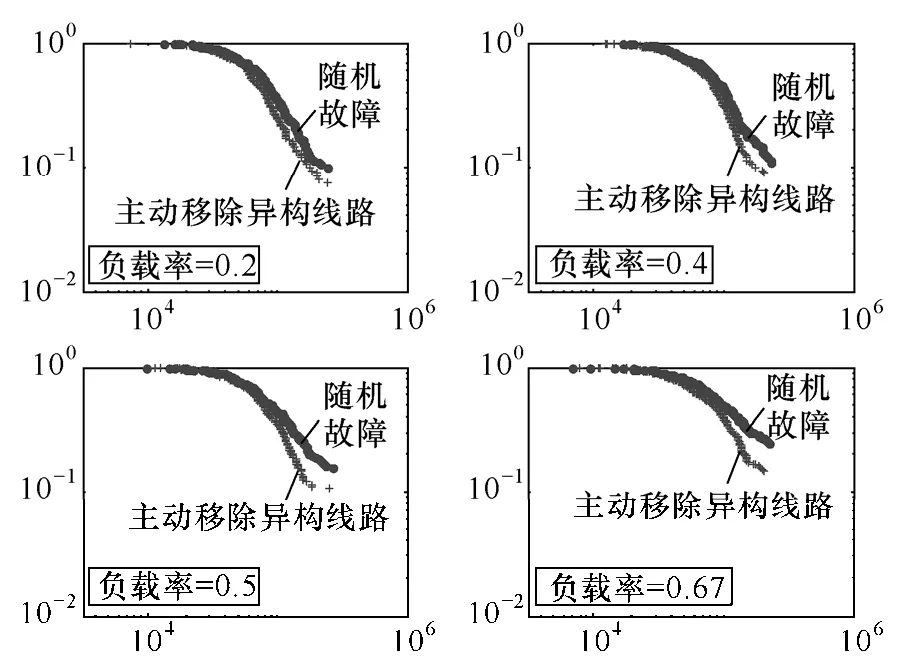
图5 华北电网损失负荷累积概率分布Fig.5 Accumulated probability distribution of power loss in north China grid
6 结论
本文基于复杂网络理论,为分析电网组织结构特性,建立了加权电网拓扑结构模型。定义了综合考虑节点和线路差异性的加权网络结构熵指标。为消除电力网络规模对结构熵的影响,采用遗传算法计算任意时刻同等规模下电网结构熵的最大值与最小值,提出了标准化电网结构熵指标。电网标准化结构熵能够分析不同时刻不同规模电力网络的异构性,可以定量评估电力系统组织结构特性对连锁故障传播的影响。
通过计算不同时刻标准化结构熵的变化并引入损失负荷百分比指标辨识电力系统“异构”线路。通过主动移除“异构”线路能优化电力网络的组织结构达到改善电网潮流分布的目的,从而提高了系统对连锁故障的抵御能力。对 IEEE 118节点系统和华北电网的仿真结果表明,按照本文提出的积极防御策略主动移除网络中某些“异构”线路能有效抑制大停电事故的蔓延,但是当电网负载率很高时,拓扑结构的改善亦不能阻止线路相继过载跳开,此时应采取措施降低系统负载率,避免大停电事故的发生。
[1] Andersson G,Donalek P,Farmer R,et al. Causes of the 2003 major grid blackouts in north america and europe,and recommended means to improve system dynamic performance[J]. IEEE Transactions on Power Systems,2005,20(4): 1922-1928.
[2] 韩祯祥,曹一家. 电力系统的安全性及防治措施[J].电网技术,2004,28(9): 1-6.
Han Zhenxiang,Cao Yijia. Power system security and its prevention[J]. Power System Technology,2004,28(9): 1-6.
[3] 薛禹胜. 综合防御由偶然故障演化为电力灾难-北美“8. 14”大停电的警示[J]. 电力系统自动化,2003,27(18): 1-5.
Xue Yusheng. The way from a simple contingency to system-wide disaster: lessons from the Eastern interconnection blackout in 2003[J]. Automation of Electric Power Systems,2003,27(18): 1-5.
[4] Bao Z J,Cao Y J,Wang G Z. Analysis of cascading failure in electric grid based on power flow entropy[J].Physica Letters A,Vol. 373,No. 3032-3040,2009.
[5] 陈晓刚,孙可,曹一家. 基于复杂网络理论的大电网结构脆弱性分析[J]. 电工技术学报,2007,22(10):138-144.
Chen Xiaogang,Sun Ke,Cao Yijia. Structural vulnerability analysis of large power grid based on complex network theory[J]. Transactions of China Electrotechnical Society,2007,22(10): 138-144.
[6] 王英英,罗毅,涂光瑜,等. 电力系统连锁故障的关联模型[J]. 电工技术学报,2012,27(2): 204-209.
Wang Yingying,Luo Yi,Tu Guangyu,et al. Correlation model ofcascading failures in power system[J].Transactions of China electro-technical society,2012,27(2): 204-209.
[7] 魏震波,刘俊勇,朱国俊. 基于可靠性加权拓扑模型下的电网脆弱性评估模型[J]. 电工技术学报,2010,25(8): 131-137.
Wei Zhenbo,Liu Junyong,Zhu Guojun. Vulnerability evaluation model to power grid based on reliabilityparameter-weighted topological model[J]. Transactions of China Electrotechnical Society,2010,25(8): 131-137.
[8] 孟仲伟,鲁宗相,宋靖雁. 中美电网的小世界拓扑模型比较分析[J],电力系统自动化,2004,28(15):21-24.
Meng Zhongwei,Lu Zongxiang,Song Jingyan. Comparison analysis of the small-world topologicalmodel of Chinese and American power grids[J]. Automation of Electric Power System,2004,28(15): 21-24.
[9] 史进,涂光瑜,罗毅. 电力系统复杂网络特性分析与模型改进[J]. 中国电机工程学报,2008,28(25):93-98.
Shi Jin,Tu Guangyu,Luo Yi. Complex network characteristic analysis and model improving of the power system[J]. Proceedings of the CSEE,2008,28(25): 93-98.
[10] 曹一家,王光增,曹丽华. 基于潮流熵的复杂电网自组织临界态判断模型[J]. 电力系统自动化,2011,35(7): 1-6.
Cao Yijia,Wang Guangzeng,Cao Lihua. An identification model for self-organized critical state of power grid based on power flow entropy[J]. Power System Technology,2011,35(7): 1-6.
[11] 徐林,王秀丽,王锡凡. 使用等值导纳进行电力系统小世界特性识别[J]. 中国电机工程学报,2009,29(19): 20-26.
Xu Lin,Wang Xiuli,Wang Xifan. Small-world feature identification based on equivalent admittance for power system[J]. Proceedings of the CSEE,2009,29(19): 20-26.
[12] 尹项根,陈庆前,王博,等. 基于四层集合模型的复杂电力系统脆弱性评估体系[J]. 电工技术学报,2013,28(1): 225-233.
Yin Xianggen,Chen Qingqian Wang Bo,et al. Vulnerability assessment system of complicated power system based on four-level set model[J]. Transactions of China Electrotechnical Society,2013,28(1): 225-233.
[13] 卢锦玲,朱永利. 基于暂态能量裕度的电力系统脆弱性评估[J]. 电工技术学报,2010,25(6): 96-103.
Lu Jinling,Zhu Yongli. Power system vulnerability assessment based on transient energy margin[J].Transactions of China Electrotechnical Society,2010,25(6): 96-103.
[14] E Bompard,R Napoli,F Xue. Analysis of structural vulnerabilities in power transmission grids[J]. International Journal of Critical Infrastructure Protection,2009,2: 5-12.
[15] 丁明,韩平平. 基于小世界拓扑模型的大型电网脆弱性评估算法[J]. 电力系统自动化,2006,30(8): 7-10.
Ding Ming,Han Pingping. Small-world topological model based vulnerability assessment algorithm for large-scale power grid[J]. Automation of Electric Power Systems,2006,30(8): 7-10.
[16] 王安斯,罗毅,涂光瑜,等. 基于事故链风险指标的输电脆弱度在线评估方法[J]. 中国电机工程学报,2010,30(25): 44-50.
Wang Ansi,Luo Yi,Tu Guangyu,et al. Online transmission vulnerability assessment method based on the fault chain risk index[J]. Proceedings of the CSEE,2010,30(25): 44-50.
[17] Kinney R,Crucitti P,Albert R,et al. Modeling cascading failures inthe North American power grid[J].The European Physical Journal,2005,46(1): 101-107.
[18] 丁明,韩平平. 加权拓扑模型下的小世界电网脆弱性评估[J]. 中国电机工程学报,2008,28(10): 20-25.
Ding Ming,Han Pingping. Vulnerability assessment to small-worldpower grid based on weighted topological model[J]. Proceedings of the CSEE,2008,28(10):20-25.
[19] 徐林,王秀丽,王锡凡. 基于电气介数的电网连锁故障传播机制与积极防御[J]. 中国电机工程学报,2010,30(13): 61-67.
Xu Lin,Wang Xiuli,Wang Xifan. Cascading failure mechanism in power grid based on electric betweenness and active defence[J]. Proceedings of the CSEE,2010,30(13): 61-67.
[20] 吴俊,谭跃进,郑宏钟,等. 无标度网络拓扑结构非均匀性研究[J]. 系统工程理论与实践,2007(5):101-105.
Wu Jun,Tan Yuejin,Deng Hongzhong,et al. Heterogeneity of scale-free network topology[J]. Systems Engineering-Theory & Practice,2007(5): 101-105.
[21] 梁才,刘文颖,温志伟,等. 电网组织结构对其自组织临界性的影响[J]. 电力系统保护与控制,2010,38(20): 6-11.
Liang Cai,Liu Wenying,Wen Zhiwei,et al. The influences of power grid structure on self-organized criticality[J]. Power System Protection and Control,2010,38(20): 6-11.
[22] 蔡晔,陈彦如,曹一家,等. 基于加权网络结构熵的电网连锁故障研究[J]. 复杂系统与复杂性科学,2013,1(10): 53-59.
Cai Ye,Chen Yanru,Cao Yijia,et al. Cascading failure in weighted power grid based on structure entropy[J]. Complex Systems and Complexity Science,2013,1(10): 53-59.
[23] Newmanm M E J,Park J. Why social networks are different from other types of networks[J] . Phys Rev E,2003,68: 036122.
[24] Wang Bing,Tang Huanwen,Guo Chonghui,et al.Entropy optimization of scale-free networks robustness to random failures[J]. Physica A,2006(363): 591-596.
[25] 邢修三. 物理熵、信息熵及其演化方程[J]. 中国科学(A辑),2001,31(1): 77-84.
Xing Xiusan. Evolvement of physics entropy and information entropy[J]. Science in China(Series A),2001,31(1): 77-84.
[26] 易俊,周孝信,肖逾男. 用连锁故障搜索算法判别系统的自组织临界状态[J]. 中国电机工程学报,2007,27(25): 1-5.
Yi Jun,Zhou Xiaoxin,Xiao Yunan. Determining the self-organized criticality state of power systems by the cascading failures searching method[J]. Proceedings of the CSEE,2007,27(25): 1-5.
