湿度对绞线正极性电晕电流脉冲及其无线电干扰影响的实验
2015-11-14卢铁兵王小波李学宝
刘 阳 崔 翔 卢铁兵 向 宇 王小波 李学宝 张 宏
(华北电力大学新能源电力系统国家重点实验室 北京 102206)
1 引言
湿度对电晕放电具有重要影响,而输电线路电晕放电引起的电磁环境能否通过评估是输电工程得以投运的必要条件,因此,湿度对电晕特性影响的研究具有重要意义。从20世纪70年代至今,国内外许多研究者就湿度对电晕特性的影响进行了广泛研究。文献[1]研究了湿度对电晕损失的影响,文献[2-12]研究了湿度对起晕电压的影响,文献[12]研究了湿度对交流电晕电流脉冲幅值与电压相位关系的影响,文献[4-8,11,13]研究了湿度对电晕电流-电压关系的影响,文献[14-16]研究了湿度对击穿特性的影响,文献[17-19]研究了湿度对臭氧产生的影响,文献[20]研究了湿度对流注发展过程的影响,文献[8]还研究了湿度对可听噪声的影响。研究结果表明,湿度对起晕电压、电晕损失和击穿电压等电晕特性均有较大影响。
在湿度对电晕电流及其无线电干扰研究方面,尽管文献[4-8,11,13]研究了湿度对电晕电流-电压关系的影响,但其电晕电流均为等效的低频稳态电流,不能反映电晕电流脉冲特性及其无线电干扰效应。迄今为止,只有少数文献涉及到湿度对电晕电流脉冲或无线电干扰的影响研究[21,22]。文献[21]利用棒板电极研究了电晕电流脉冲的峰值、重复频率随湿度的变化关系,其采用的棒板电极具有的间隙仅4cm,能产生电晕电流脉冲的电压范围十分有限,得到的测量数据也很少。此外,棒板的短间隙电晕放电与实际线路电晕放电差异较大。因此,该研究存在一定局限性。文献[22]在步入式环境气候小室利用直径 0.5mm的细铜线作为试验线段研究了温度和湿度对交流电晕无线电干扰的影响,其测量结果表明:温度一定时,随着相对湿度升高,无线电干扰明显降低。然而,该研究仅对 0.5MHz的无线电干扰进行了频域测量,并未涉及电晕电流脉冲的测量,不能从电晕电流脉冲的层面揭示湿度对无线电干扰的影响机理。而且,由于直流电晕与交流电晕存在本质差异,该结论对于直流电晕是否适用尚未可知。
综上所述,在湿度对电晕电流脉冲特性及其无线电干扰的影响研究方面,尚无全面深入的研究工作。其原因在于,一方面由于一般试验导线的终端开路,试验导线上的电晕电流经多次反射与叠加,导致测量到的电晕电流已不再是电晕放电的初始电流,不能准确反映电晕电流脉冲的真实性;另一方面,电晕电流脉冲产生的无线电干扰、受外界其他无线电干扰的影响或在实验室内部受地面和墙壁多次反射的影响,不能准确全面反映电晕电流脉冲直接产生的无线电干扰。这些都客观地造成了研究湿度对电晕电流脉冲及其无线电干扰影响的困难。
本文通过采用试验导线终端匹配技术克服了上述困难,准确测量直流绞线上的电晕电流脉冲,研究湿度对其特性的影响,进而研究对无线电干扰的影响。不同于文献[21,22]的实验方法,本文采用同轴圆柱结构电晕笼来产生电晕,并以绞线作为起晕导线,以获得与实际情况更为接近的导线电晕放电。在电晕电流脉冲的测量方面,现有文献方法由于未能解决试验导线的阻抗匹配问题,测量到的电晕电流波形因多次反射而发生畸变,造成现有文献未能给出电流脉冲的波形参数如上升时间、半峰值时间及持续时间等随湿度的变化关系[21,22]。本文设计了一种阻抗匹配的电晕电流测量方法,准确测量了绞线上电晕电流脉冲的初始波形[23]。通过对电晕电流脉冲的峰值概率密度分布、平均峰值、重复频率、上升时间、半峰值时间和持续时间等进行统计和分析,得到了湿度对电晕电流脉冲特性的影响规律。进一步地利用Welch方法[24],建立了电晕电流脉冲功率谱的计算方法。通过分析湿度对电晕电流脉冲功率谱的影响,进而获得了湿度对直流绞线无线电干扰的影响规律。
2 实验平台
2.1 绞线电晕放电实验平台
对于双极直流输电线路而言,在同样的电压下,由于负极性导线电晕产生的无线电干扰低于正极性导线电晕,即正极性导线电晕电流脉冲是无线电干扰的主导原因,因此,本文搭建了一个绞线正极性电晕放电实验平台,如图1所示。绞线的电晕放电在同轴圆柱电晕笼内进行,其笼体由 30根圆柱形导体棒围成,在两端由均压环固定。为使绞线产生正极性电晕放电,实验中在笼体上加负极性直流高压,中心绞线接地。此时,绞线相对于笼体为正电压,由于绞线表面场强最高,当电压足够高时绞线表面就会发生正极性电晕放电。之所以采用此加压方式,是为了便于利用本文作者在文献[23]中提出的测量方法,即试验导线两端通过匹配电阻接地。该测量方法较好地消除了电晕电流脉冲在试验导线端部的反射问题,可准确得到试验导线上电晕电流脉冲的初始波形。在本文实验中,导线采用直径为1mm的绞线,电晕笼直径为60cm,笼子长度为1.5m。为保证绞线表面状态的一致性,在搭建实验平台的过程中对其表面进行了精心的保护,以避免碰到任何硬物破坏其表面状态。采用美国 Tektronix公司的TCP312电流探头对试验导线上的电晕电流脉冲进行测量,该电流探头的带宽为DC~100MHz。并采用荷兰TiePie公司的HS5—530XM采集卡对电晕电流脉冲信号进行采集和记录,该采集卡采样频率可调,最高可达 500MHz;双通道,每个通道的存储深度为32M(此处1M=1 024×1 024)个采样点。考虑到直流电晕电流脉冲的频带宽度一般为 DC~30MHz,本文采用了200MHz的采样频率,因此每次采样的时间长度可达167.8ms。在每种实验条件下,采样 10次,将所有电晕电流脉冲进行统计即可得到1.678s长时间尺度下的脉冲。需指出,一次采样后需一定时间完成存储,之后才能进行下一次采样,尽管在存储期间的电晕电流脉冲被遗漏掉了,但是,由于电晕过程是一个平稳随机过程,10次采样的电晕电流脉冲是可以表征长时间的电晕电流脉冲特性的。
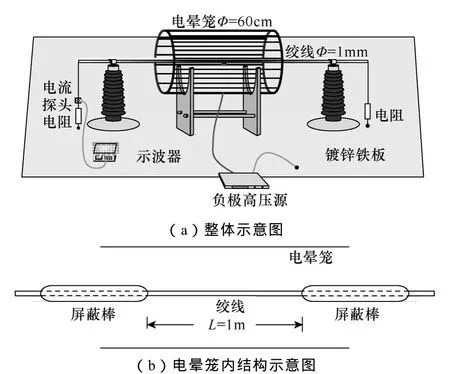
图1 绞线电晕放电实验平台Fig.1 The layout of the experimental setup for corona discharge
为了消除电晕笼的边缘效应,试验绞线的两端套装了直径为8mm的穿孔金属棒,如图1b所示。穿孔金属棒的两端设计成半圆球状,防止起晕。试验绞线的起晕部分位于电晕笼中间 1m的区域内,保证了轴向电场的均匀性。
2.2 湿度控制
实验平台位于封闭的室内,通过加湿器来实现对湿度的控制。室内空间较大,面积约 104m2,高度约3m,利于水蒸气的充分扩散,获得较高的均匀度。相对湿度从40%往上逐渐增加,若湿度到达指定值时,即停止加热并将水蒸气源移至室外。为保证湿度的均匀性,湿度调节完成后需要等待10min,待水汽均匀扩散后,进行各电压条件下的电晕电流测量。每种湿度条件下测量工作所需时间约为30min。实验过程中,记录了温湿度条件,见表1。由表1可见,相对湿度与设定值偏差较小,波动在±2%以内;整个实验过程中,温度变化范围为 27.7~28.1℃,可认为温度变化带来的影响远小于湿度。

表1 实验的温度和湿度条件Tab.1 The temperature and humidity conditions of the experiment
3 电晕电流脉冲的实验结果及分析
图2给出了电压为40kV时,不同湿度下50ms内电晕电流脉冲的典型波形。图3为放大后的局部图。其中i表示电流值,mA;t表示时间,ms;H表示相对湿度(%);U表示电压,kV。以上变量均与下文相同。由图2可知,湿度不同时,相同电压下电晕电流脉冲的时域分布特征有较大不同。峰值、峰值概率密度、重复频率和波形参数是电晕电流脉冲的重要表征参数,与无线电干扰密切相关。下面将对它们进行统计分析。
3.1 电晕电流脉冲的提取方法
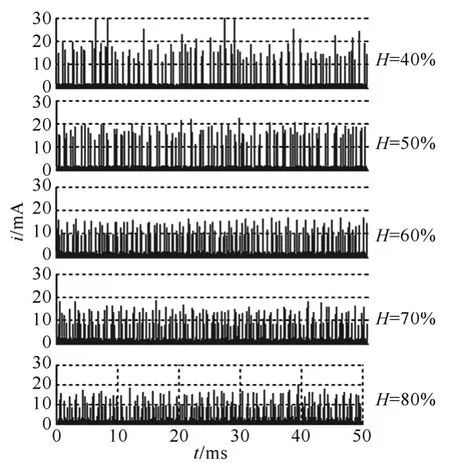
图2U=40kV时电晕电流脉冲典型波形Fig.2 The typical waveform of corona pulses atU=40kV
由于电流探头与采集卡构成的测量系统本身存在背景噪声,如图3所示。通过分析发现,背景噪声信号落在-2~2mA范围内。为最大程度地挑选出所有电晕电流脉冲,本文选取2mA作为脉冲判断的临界值,当脉冲的峰值超过2mA时,则对其进行统计。
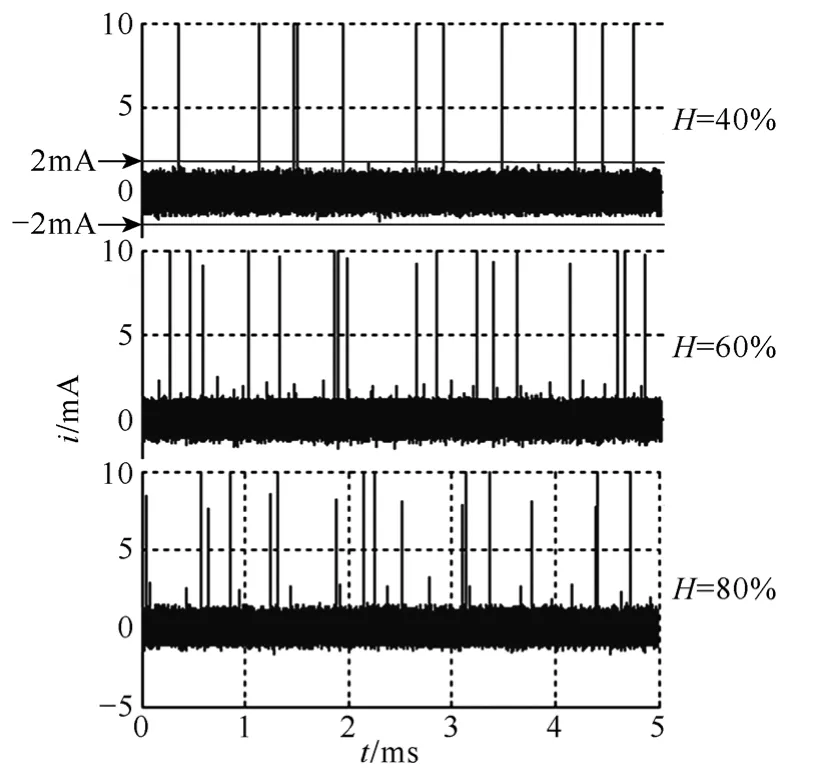
图3U=40kV时电晕电流脉冲分布特征局部放大图Fig.3 The drawings of partial enlargement of the waveform of corona pulses atU=40kV
3.2 电晕电流脉冲峰值的概率密度分布
电晕电流脉冲峰值的概率密度分布可给出峰值位于某一区间内的脉冲的密集程度,能较好地反映脉冲峰值和重复频率特征。本文采用核密度估计方法来确定脉冲峰值的概率密度函数。核密度估计方法是一种非参数估计方法,它相比于直方图估计的好处是密度函数可表达成一条曲线。利用该方法获得的40kV时脉冲峰值的概率密度分布如图4所示。
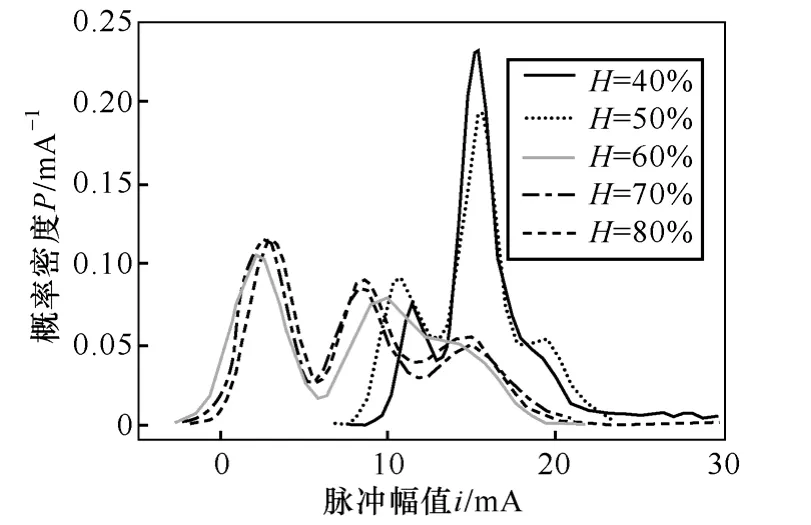
图4U=40kV时不同湿度下电晕电流脉冲的峰值概率密度分布Fig.4 The distribution of probability density of corona current pulse amplitude under different humidity conditions atU=40kV
由图4可见,电流脉冲峰值的概率密度呈现多峰分布。实验观测表明,单个放电点产生的电晕电流脉冲的峰值概率密度呈现钟形分布[25,26]。由于绞线上存在多个放电点,所以这正好解释了概率密度分布的多峰特征。
图4还表明,峰值概率密度分布在不同湿度条件下会发生明显不同。由于它具有多峰特征,本文将按各峰分别给出平均峰值、方差及重复频率。由于单个放电点产生的电晕电流脉冲的峰值概率密度分布呈单峰特性,表明其脉冲峰值水平较为固定,仅在平均值附近有一定波动,近似满足正态分布。所以,电晕电流脉冲的概率密度分布可近似由多个正态分布叠加而成。本文称这种拟合为多正态分布拟合,即按式(1)对其进行拟合。
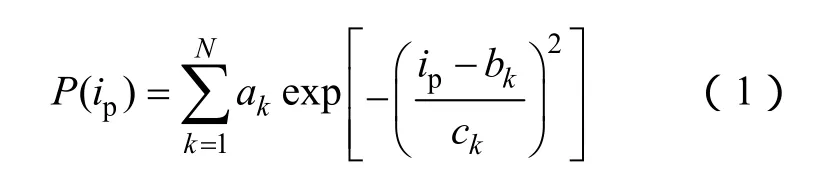
式中,ip为电晕电流脉冲峰值,mA;P为概率密度,mA-1,表示1mA区间内脉冲个数占总脉冲个数的比例;N为概率密度曲线峰的个数;ak、bk、ck均为常系数,通过拟合确定;exp表示以自然常数 e为底的指数函数。
图5给出了电压为40kV,湿度为60%的峰值概率密度及其拟合曲线。该概率密度分布曲线有3个峰,因此N取 3。拟合得到的各参数见表 2。由图可见,拟合曲线与统计得到的曲线基本重合,拟合效果较理想。
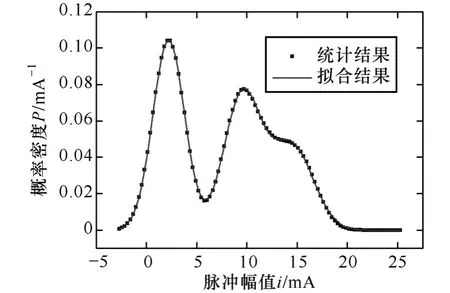
图5U=40kV、H=60%时的峰值概率密度分布的多正态分布拟合Fig.5 The fitting results of probability density function of amplitude using multi-normal distribution atU=40kV,H=60%
对所有湿度和电压条件下电晕电流脉冲的峰值概率密度曲线按上述方法进行拟合,可得到拟合系数。由拟合系数易得到各峰所含电晕电流脉冲的峰值平均值及方差和脉冲数(总脉冲个数乘以峰与x轴围成的面积),结果见表3。其中,u表示各峰所含电晕电流脉冲的峰值平均值,mA;σ表示各峰所含电晕电流脉冲峰值的方差,mA;R表示各峰所含电晕电流脉冲的重复频率,kHz。

表2 各系数的拟合结果Tab.2 The fitting results of the coefficients
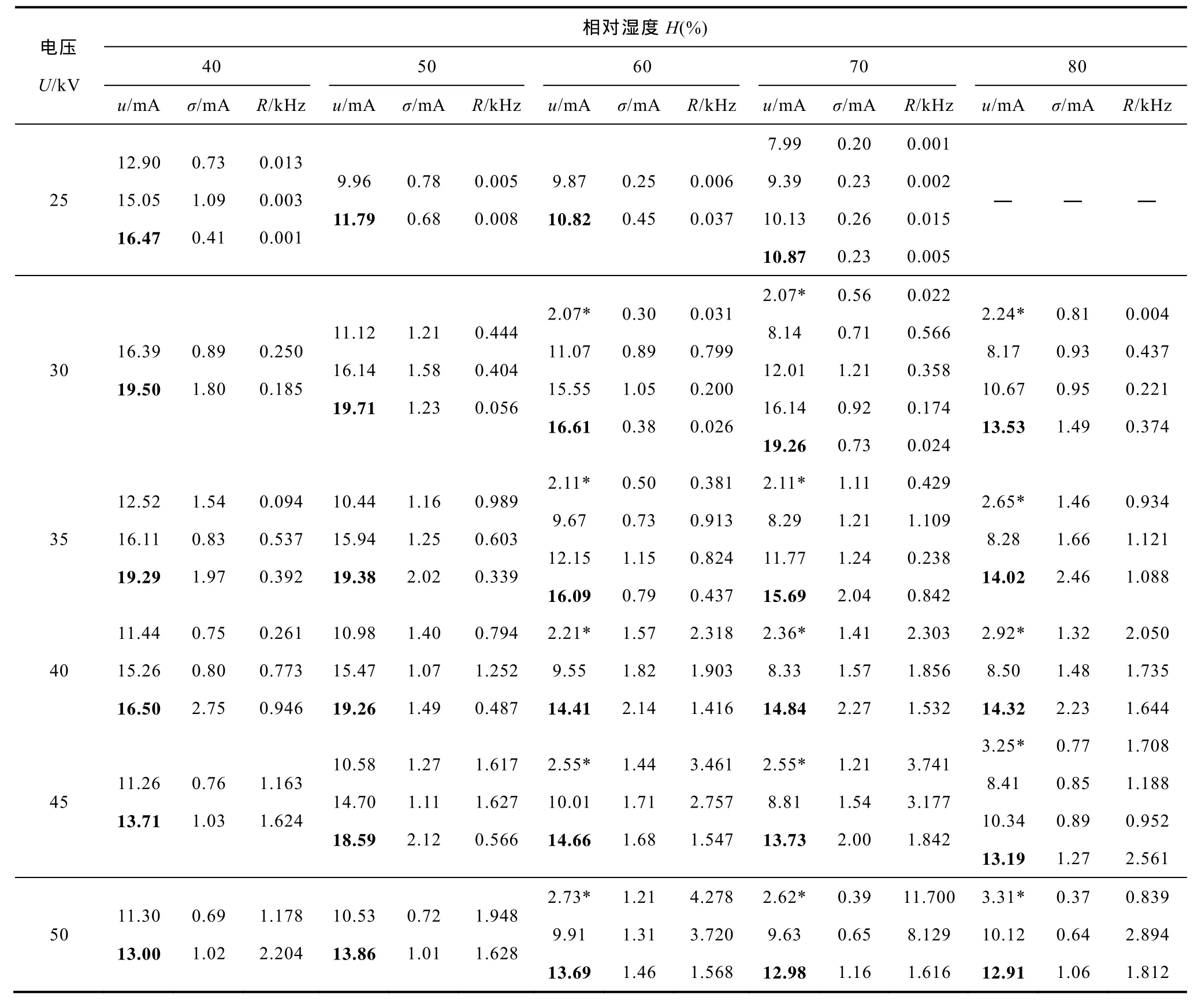
表3 电晕电流脉冲峰值的概率密度分布特征参数Tab.3 The characteristic parameters of probability density of corona current pulse amplitude
由表3可见,在相对湿度高于60%且电压大于30kV时,有小峰值脉冲出现,其平均峰值约为2~4mA,表中用带“*”的数字表示。这是因为,空气中的水分子大部分以水分子团的形式存在,水分子团具备一定的体积,它们附着于绞线表面时,就会形成新放电点。当湿度升高时,水分子团的数量增多,就更易形成新放电点。由于水分子团体积相对于绞线表面其他固有的放电点(非水分子团形成的放电点)很小,它们形成的新放电点附近电场的均匀性较好,导致电离区仅局限于很小的一块区域,所以新放电点产生的脉冲峰值很小。新放电点附近的电场不均匀程度较固有放电点低,要到达起晕场强所需要的电压更高,因此,它们发生流注放电也需要更高的电压。所以在电压小于 30kV时,其他放电点已经产生了电晕电流脉冲,而这些新放电点尚未产生电晕电流脉冲。
由于大峰值脉冲对无线电干扰有较大贡献,表3中将u的最大值用加粗数字表示,记为umax。umax随湿度的变化规律较复杂。当湿度小于50%时,无相同规律。当湿度不小于 50%时,umax总体上随湿度升高而降低,仅在湿度70%、电压为25kV和30kV时出现相反的情况。湿度升高,峰值减小的原因是,电子-正离子复合系数βep随湿度升高而增加[27],电离区内的电子更易与正离子复合而消失。而电晕电流脉冲主要是由电离区中的电子在电场加速作用下形成,因此电晕电流脉冲峰值会减小。另一个重要原因是,当水分子形成的放电点靠近固有放电点时,会对固有放电点形成一定屏蔽,从而使固有放电点的放电过程减弱,所以脉冲峰值减小。然而,湿度70%、电压为25kV和30kV时出现相反的规律,说明存在其他因素的影响,作者尚不能给出合理解释,有待进一步研究。
3.3 电晕电流脉冲的平均峰值
由于湿度增加后,新的放电点会形成,并产生许多小峰值脉冲,如图3所示。这些脉冲的峰值(2~4mA)明显小于其他固有放电点的脉冲峰值(8~20mA)。所以,若把它们计入平均值的计算,平均峰值将受到很大影响。然而,小峰值脉冲对无线电干扰的贡献却十分有限。因此,为准确反映无线电干扰的效应,在统计脉冲峰值的平均值时,需剔除这些小脉冲。根据脉冲峰值的特点,5mA可以作为这些小脉冲和其他脉冲的界限。因此,本文将脉冲平均峰值定义为峰值超过 5mA的脉冲的峰值平均值。
峰值平均值的结果如图6所示。可见平均峰值总体上随湿度的增加呈减小趋势。其原因在 3.2节中已作解释。
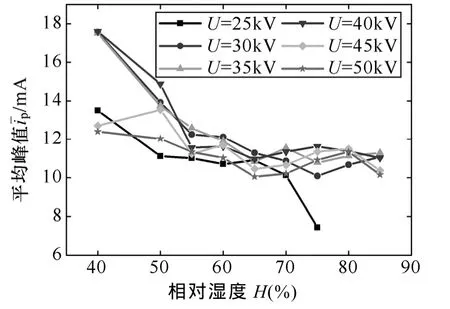
图6 平均峰值随湿度的变化关系Fig.6 The variation of the pulses’ average amplitude with humidity
3.4 电晕电流脉冲的重复频率
小峰值脉冲对脉冲重复频率的统计有较大影响,然而它们对无线电干扰影响甚微,鉴于此,在统计脉冲的重复频率时,需要剔除这些小脉冲。与平均峰值的定义类似,本文将脉冲重复频率定义为1s内的峰值超过5mA的脉冲数。
图7给出了湿度变化时,脉冲重复频率的变化。由图可知,随着湿度增加,脉冲重复频率先增大后减小。这是因为,湿度增加时,βep增加[27],这意味着,电离区中的大量正离子与电子发生复合而消失。一次放电结束后,空间中遗留的正离子密度将减小,所以正离子向电晕笼体驱散使导线表面电场恢复下一次起晕条件的过程将更快。因此,当湿度增加时,电晕电流脉冲的重复频率会先增加。
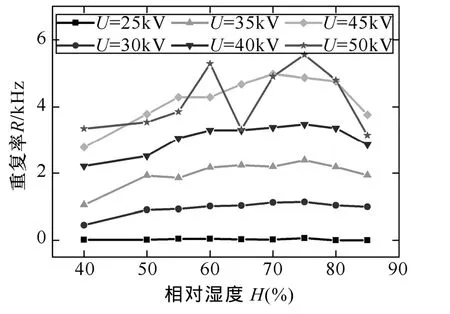
图7 脉冲重复频率随湿度的变化Fig.7 The dependence of repetition rate of corona pulse on the humidity
然而,当湿度进一步增加时,重复频率会减小。当空气中存在水分子时,正离子与水分子会结合成为水合正离子[28],水合离子的质量较常规离子大,所以正离子迁移率减小。因此,正离子驱散使得下一次放电条件的恢复需要花费更多时间。湿度增加时,正离子与水分子结合将更易发生,当这一因素占据主导时,重复频率就会降低。
电压为50kV时,当湿度增加到 65%时,脉冲的重复频率出现突降。这是因为当电压足够高时,电晕放电将转入下一个稳定的、放电阶段——正极性辉光放电,此阶段的电晕电流由直流分量叠加以小峰值脉冲组成[29],所以重复频率降低。
3.5 脉冲的波形参数
脉冲的波形反映了放电点附近电场的分布情况,决定着无线电干扰的频谱特性。脉冲波形通常由上升时间、半峰值时间和持续时间来表征。参考雷电波波形参数定义及文献[30]中关于电晕电流波形参数的定义,本文以一个实测电晕电流脉冲波形为例,给出了最终定义,如图8所示。其中,Tr表示上升时间;Tf表示半峰值时间;Td表示持续时间。需要说明的是,受背景噪声的影响,小峰值脉冲的波形难以分辨出上述3个波形参数,同时考虑到小峰值脉冲对无线电干扰贡献很小,本文仅对峰值大于5mA的脉冲进行统计。
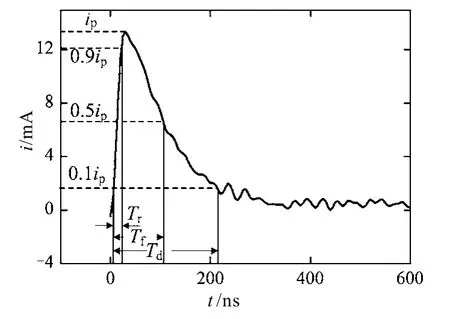
图8 电流脉冲波形参数的定义Fig.8 The definition of waveform parameters of the corona current pulse
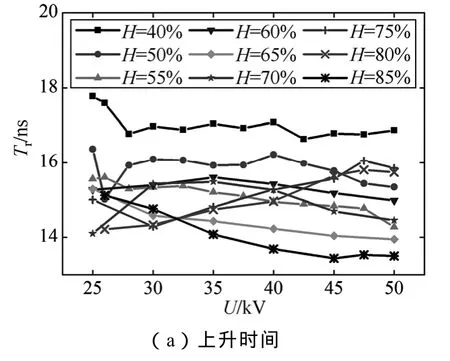
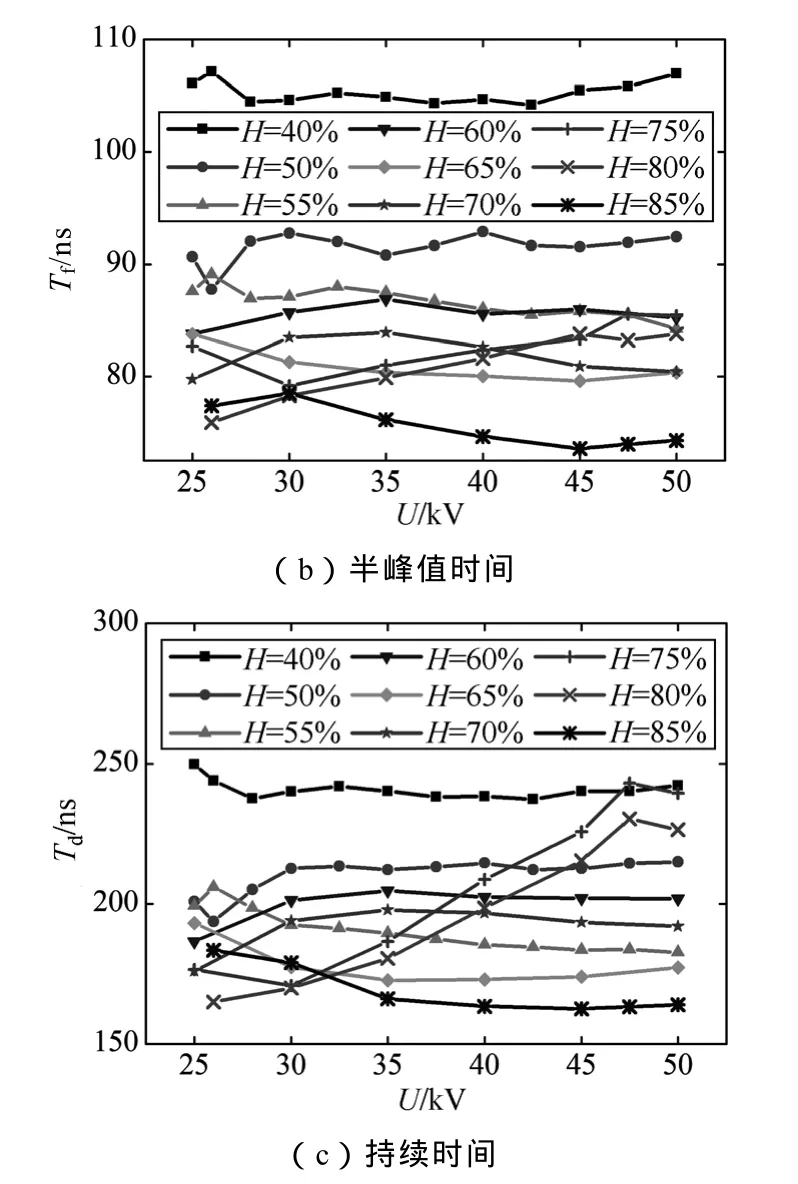
图9 电流脉冲波形参数的统计特征Fig.9 The statistical characteristics of waveform parameters of corona current pulse
4 电晕电流脉冲功率谱的计算及结果分析
由于电晕电流为随机信号,在无线电干扰理论分析中通常采用其功率谱进行分析,如激发函数理论就采用了这一概念。它反映了无线电干扰在特定频段的有效值水平,是无线电干扰理论分析中最直接的表征量。为研究湿度对无线电干扰的影响,本节分析了湿度对电晕电流功率谱的影响。
4.1 无线电干扰与电晕电流功率谱之间的联系
实际工程中,通常采用环状天线来测量无线电干扰,其测量的物理量实际为磁场。对于如图 10所示的N导体输电线路,地面处磁场的水平分量可表示为
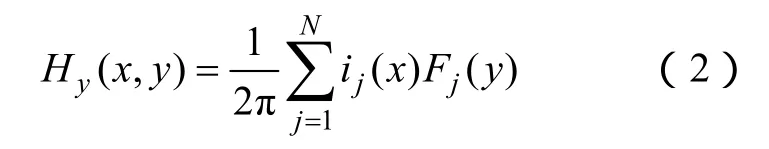
式中,ij为第j根导线上的电流,以x轴正方向为参考方向;Fj为场系数,其表达式为
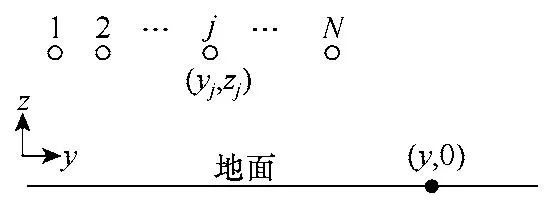
图10N导体输电线路示意图Fig.10 The diagram of theN-conductor transmission line
式中,p为磁场透入深度,其表达式参见文献[31]。
由式(3)可知,无线电干扰与电晕电流呈正比。因此本文将采用电晕电流的功率谱来表征无线电干扰的强弱。
4.2 电晕电流脉冲功率谱的计算方法
本文采用Welch法[24]计算功率谱密度。该方法采用了信号重叠分段、加窗函数和FFT算法等技术,有效降低了谱估计的方差,同时又不使分辨力遭到严重破坏,是一种有效的谱估计方法。Welch法包括两个步骤。首先将电流信号i(n)分成P段,x1,x2,…,xP,每段M个数据,数据段之间允许一定程度的重合。则第p段信号的功率谱Sp可表示为
同理,得出座椅处在4种不同车速下奇异值差分谱的关系,如图8所示.由图8中的值,可以确定在不同车速下奇异值的重构阶数.
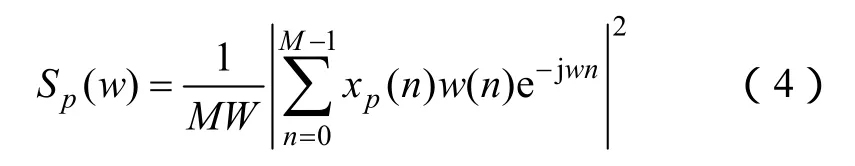
式中,W为归一化因子,;w(n)为所加的窗函数,本文选用Hamming窗,该窗函数具有旁瓣衰减较大、噪声水平低等优点。其次,将P段数据得到的功率谱进行平均,即可得到电晕电流的功率谱
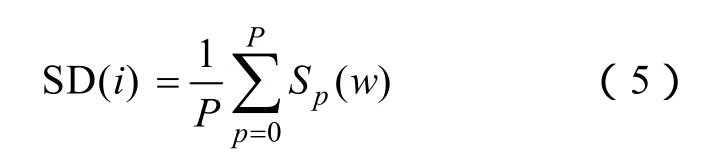
4.3 电晕电流功率谱计算结果及分析
图11给出了电晕电流0.5MHz功率谱密度随湿度的变化情况。SD(i)表示电晕电流的0.5MHz功率谱密度,dB(nA2/m)。由图可见,随着湿度的增加,电晕电流的功率谱逐渐减小。
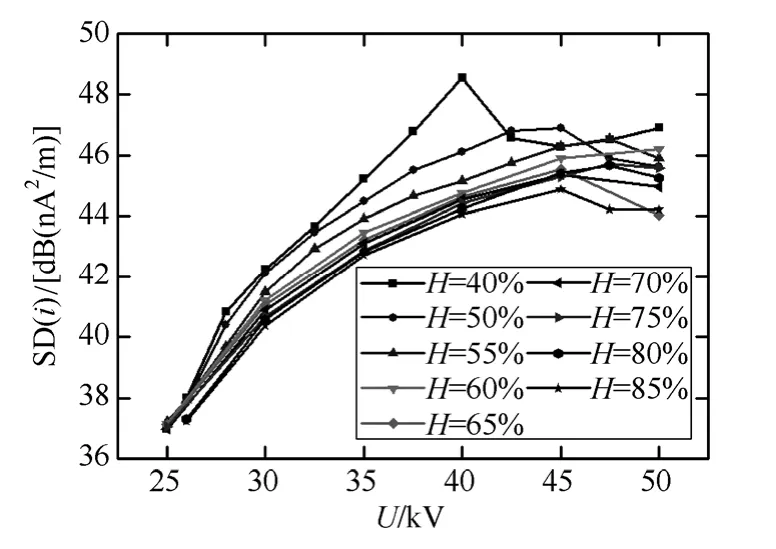
图11 电晕电流功率谱随湿度的变化关系Fig.11 The dependence of spectral density of the corona current on humidity
当相对湿度小于60%时,湿度对电晕电流功率谱的影响较大;当相对湿度不小于60%时,湿度对电晕电流功率谱的影响较小。图12给出了30kV、35kV、40kV时,以相对湿度 85%的值作为基准,不同湿度条件的修正值。其中,ΔSD表示不同湿度下电晕电流0.5MHz功率谱的修正值。从图12可见,电压较高时,湿度对电晕电流功率谱影响较显著。例如,40kV条件下,相对湿度40%时的功率谱值比85%的大 4.5dB,这意味着,相对湿度 40%时的无线电干扰场强值是85%的1.68倍。电压较低时,影响稍弱,例如,在电压为 30kV时,相对湿度40%时的功率谱值比85%的大2dB。这意味着,相对湿度40%时的无线电干扰场强值是85%的1.26倍;然而,相对湿度为55%以上时,修正值均在1.2dB以下,无线电干扰场强值的相对差异在15%以内。
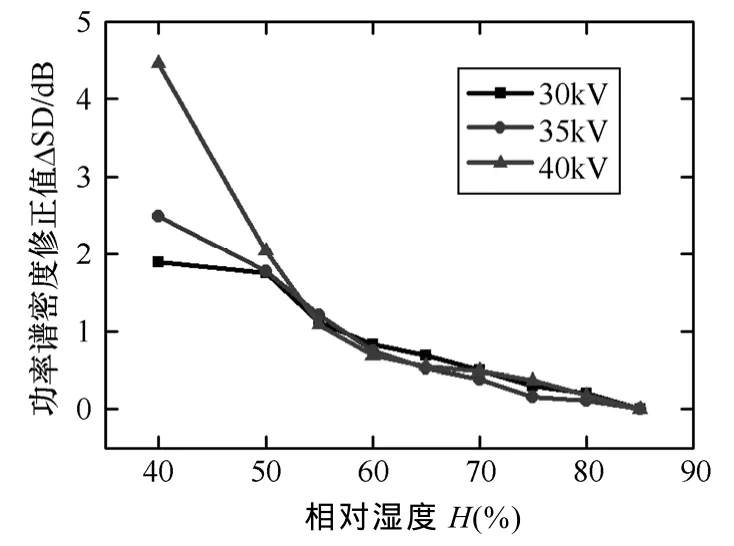
图12 不同湿度下功率谱的修正值Fig.12 Correction value for spectral density of corona current under different humidity conditions
5 分析与讨论
相关研究成果表明,无线电干扰准峰值与脉冲峰值和重复频率近似满足关系[32]

式中,RI为无线电干扰;k为常系数;R和ip的含义同上文。从式(6)可见,脉冲的无线电干扰效应与ip的关联性较强,与R的关联性稍弱。
由上文知,湿度增加时,平均峰值减小,说明无线电干扰效应减弱。但是,重复频率先增加后减小。为了同时考虑二者影响,对图6、图7中的峰值和重复频率按式(6)进行计算,将RI作归一化处理,仅比较ipR0.44的数值。计算结果如图13所示。可见,在40kV及以下时,RI随湿度增加存在一定的减小趋势。说明在峰值减小和重复频率先增加后减小两个因素共同作用下,无线电干扰将减小。这刚好解释了在第4节中根据电晕电流功率谱得到的结论:湿度增加会使无线电干扰减小。
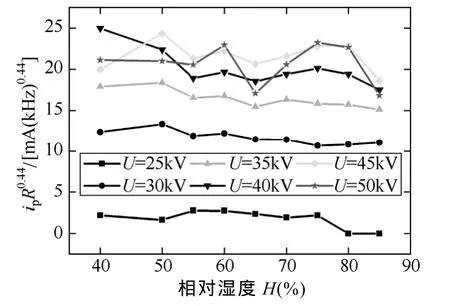
图13RI的归一化比较Fig.13 The comparison of normalization value ofRI
另外,理论分析表明,无线电干扰与脉冲宽度具有线性关系[33,34]。湿度增加时,脉冲的持续时间会减小,这也将使无线电干扰效应减弱。
P. S. Maruvada 等[35-38]对 DC±600~±1200kV的试验线段及电晕笼进行了长期监测,测量结果表明,直流导线电晕产生的无线电干扰,晴天比雨天或阴天大。晴天湿度通常小于雨天或阴天,所以,本文研究恰好解释了这一现象。
6 结论
本文搭建了小尺寸正极直流绞线电晕放电实验平台,就湿度对正极性电晕电流脉冲及其无线电干扰的影响规律进行了探索。通过对脉冲峰值概率密度、平均峰值、重复频率、波形参数及功率谱的分析,得到以下结论:
(1)绞线的电晕电流脉冲的峰值概率密度呈多峰分布;随着湿度的增加,电晕电流脉冲的平均峰值减小;电晕电流脉冲的重复频率先增加后减小,在60%~75%范围内最大;40%~60%范围内电晕电流脉冲的上升时间、半峰值时间、持续时间明显减小,在60%~85%的范围内无明显规律。
(2)随着湿度的增加,正极性直流电晕电流脉冲的功率谱减小,证实了湿度是造成晴天直流无线电干扰较雨天和阴天大的一个重要因素。
(3)湿度小于55%时,湿度对功率谱的影响较为显著;湿度大于等于55%时,湿度对功率谱的影响较小;起晕程度越强,湿度的影响越大。
[1] Khalifa M,El-Debeiky S. Analysis of the effect of humidity on d. c. corona power losses[J]. Proceedings of the Institution of Electrical Engineers,1971,118(5):714-718.
[2] Allen N L,Berger G,Dring D,et al. Effects of humidity on corona inception in a diverging electric field[J].IEE Proceedings of a Physical Science,Measurement and Instrumentation,Management and Education-Reviews,1981,128(8): 565-570.
[3] Fouad L,Elhazek S. Effect of humidity on positive corona discharge in a three electrode system[J]. Journal of Electrostatics,1995,35(1): 21-30.
[4] Bian X M,Meng X B,Wang L M,et al. Negative corona inception voltages in rod-plane gaps at various air pressures and humidities[J]. IEEE Transactions on Dielectrics and Electrical Insulation,2011,18(2):613-619.
[5] 惠建峰,关志成,王黎明,等. 正直流电晕特性随气压和湿度变化的研究[J]. 中国电机工程学报,2007,27(33): 53-58.
Hui Jianfeng,Guan Zhicheng,Wang Liming,et al.Research on variation of positive DC corona characterristics with air pressure and humidity[J]. Proceedings of the CSEE,2007,27(33): 53-58.
[6] 卞星明,惠建峰,黄海鲲,等. 气压湿度对负直流电晕特性影响的研究[J]. 中国电机工程学报,2010,30(4): 118-124.
Bian Xingming,Hui Jianfeng,Huang Haikun,et al.Effects of air pressure and humidity on the charateristics of negative DC corona[J]. Proceedings of the CSEE,2010,30(4): 118-124.
[7] Bian X M,Wang L M,MacAlpine J M K,et al.Positive corona inception voltages and corona currents for air at various pressures and humidities[J]. IEEE Transactions on Dielectrics and Electrical Insulation,2010,17(1): 63-70.
[8] 安冰,丁燕生,王伟,等. 湿度对电晕笼中导线直流电晕特性的影响[J]. 电网技术,2008,32(24):98-101.
An Bing,Ding Yansheng,Wang Wei,et al. Influence of humidity on corona performance of DC conductor in corona cage[J]. Power System Technology,2008,32(24): 98-101.
[9] Hu Q,Shu L,Jiang X,et al. Effects of air pressure and humidity on the corona onset voltage of bundle conductors[J]. IET Generation,Transmission & Distribution,2011,5(6): 621-629.
[10] Xu M M,Tan Z Y,Li K J. Modified Peek formula for calculating positive DC corona inception electric field under variable humidity[J]. IEEE Transactions on Dielectrics and Electrical Insulation,2012,19(4):1377-1382.
[11] Wang X H,You C F. Effect of humidity on negative corona discharge of electrostatic precipitators[J]. IEEE Transactions on Dielectrics and Electrical Insulation,2013,20(5): 1720-1726.
[12] Meng X B,Hui J F,Mei H W,et al. Influence of pressure and humidity on the amplitude-phase distribution of AC corona pulse[C]. Annual Report Conference on Electrical Insulation and Dielectric Phenomena,2013: 838-841.
[13] Nouri H,Zouzou N,Moreau E,et al. Effect of relative humidity on current-voltage characteristics of an electrostatic precipitator[J]. Journal of Electrostatics,2012,70(1): 20-24.
[14] Allen N L. Corona,breakdown and humidity in the rodplane gap[J]. IEE Proceedings a Physical Science,Measurement and Instrumentation,Management and Education-Reviews,1986,133(8): 562-568.
[15] Boutlendj M,Allen N L,Lightfoot H A,et al. Positive DC corona and sparkover in short and long rod-plane gaps under variable humidity conditions[J]. IEE Proc.–A,1991,138(1): 31-36.
[16] Rodriguez D,Gorur R S,Hansen P M. Effect of humidity on the breakdown characteristics of air in non-uniform fields at 30kHz[J]. IEEE Transactions on Dielectrics and Electrical Insulation,2010,17(1):45-52.
[17] Peyrous R. The effects of relative humidity on ozone production by corona discharge in oxygen or air-a numerical simulation-part I: oxygen[J]. Ozone Science and Engineering,1990,12(1): 19-40.
[18] Peyrous R. The effects of relative humidity on ozone production by corona discharge in oxygen or air-a numerical simulation-part II: air[J]. Ozone Science and Engineering,1990,12(1): 41-64.
[19] Chen J,Wang P. Effect of relative humidity on electron distribution and ozone production by DC coronas in air[J]. IEEE Transactions on Plasma Science,2005,33(2): 808-812.
[20] Hui J F,Guan Z C,Wang L M,et al. Variation of the dynamics of positive streamer with pressure and humidity in air[J]. IEEE Transactions on Dielectrics and Electrical Insulation,2008,15(2): 382-389.
[21] 卞星明,惠建峰,黄海鲲,等. 气压和湿度对正直流电晕流注脉冲特性的影响[J]. 高电压技术,2009,35(10): 2371-2382.
Bian Xingming,Hui Jianfeng,Huang Haikun,et al.Influence of air pressure and humidity on positive DC corona streamer pulse characteristics[J]. High Voltage Engineering,2009,35(10): 2371-2382.
[22] 蒋虹,陈豫朝,张广洲,等. 温湿度对交流电晕无线电干扰的影响[J]. 高电压技术,2011,37(12):2918-2923.
Jiang Hong,Chen Yuchao,Zhang Guangzhou,et al.Effect of temperature and humidity on radio interference generated from AC corona[J]. High Voltage Engineering,2011,37(12): 2918-2923.
[23] Liu Yang,Cui Xiang,Lu Tiebing,et al. Accurate measurement of original current pulses because of positive corona in the coaxial cylindrical arrangement[J]. IET Science,Measurement & Technology,accepted.
[24] 张峰,石现峰,张学智. Welch功率谱估计算法仿真及分析[J]. 西安工业大学学报,2009,29(4): 353-356.
Zhang Feng,Shi Xianfeng,Zhang Xuezhi. Study and simulation of Welch power spectrum estimation method[J]. Journal of Xi’an Technological University,2009,29(4): 353-356.
[25] Malik N H,Al-rainy A A. Statistical variation of DC corona pulse amplitudes in point-to-plane air gaps[J].IEEE Transactions on Electrical Insulation,1987,EI-22(6): 825-829.
[26] Maruvada P S. Corona performance of high-voltage transmission lines[M]. Baldock: Research Studies Press,2000.
[27] Chervenak J G,Van Lint V A J. Electron-ion recombination in air at EMP fields[J]. IEEE Transactions on Nuclear Science,1985,32(6): 4308-4311.
[28] Sakata S,Okada T. Effect of humidity on hydrated cluster-ion formation in a clean room corona discharge neutralizer[J]. Journal of Aerosol Science,1994,25(5):879-893.
[29] Trinh N G. Partial discharge XIX: Discharge in air Part I: Physical mechanisms[J]. IEEE Electrical Insulation Magazine,1995,11(2): 23-29.
[30] Otto A J. Direct current conductor corona modeling and metrology:[D]. Stellenbosch,South Africa: University of Stellenbosch,2009.
[31] DL/T 691-1999,高压架空送电线路无线电干扰计算方法[S].
[32] Liao T W,Keen W A,Powell D R. Relationship between corona and radio influence on transmission lines,laboratory studies I-point and conductor corona[J]. Transactions of the American Institute of Electrical Engineers on Power Apparatus and Systems,Part III,1954,76(3): 530-538.
[33] Nigol O. Analysis of radio noise from high-voltage lines I-meter response to corona pulses[J]. IEEE Transactions on Power Apparatus and Systems,1964,83(5): 524-533.
[34] Maruvada P S,Hylten-Cavallius N,Chinh N T. Radio noise meter response to random pulses by computer simulation[J]. IEEE Transactions on Power Apparatus and Systems,1974,93(3): 905-915.
[35] Maruvada P S,Trinh N G,Dallaire D,et al. Corona performance of a conductor bundle for bipolar HVDC transmission at ±750kV[J]. IEEE Transactions on Power Apparatus and Systems,1977,96(6): 1872-1882.
[36] Maruvada P S,Trinh N G,Dallaire R D,et al. Corona studies for bipolar HVDC transmission at voltages between ±600kV and ±1 200kV Part 1: Long-term bipolar line studies[J]. IEEE Transactions on Power Apparatus and Systems,1981,100(3): 1453-1461.
[37] Maruvada P S,Dallarie R D,Heroux P,et al. Corona studies for bipolar HVDC transmission at voltages between ±600kV and ±1200kV Part 2: Special bipolar line,bipolar cage and bus studies[J]. IEEE Transactions on Power Apparatus and Systems,1981,100(3): 1462-1471.
[38] Maruvada P S,Dallaire R D,Heroux P,et al. Longterm statistical study of the corona electrical field and ion-current performance of a ±900kV bipolar HVDC transmission line configuration[J]. IEEE Power Engineering Review,1984,4(1): 33-33.
