基于固定码本的分形图像编码算法

袁宗文 鲁业频 杨汉生

（巢湖学院机械与电子工程学院，安徽 巢湖 238000）

基于固定码本的分形图像编码算法

袁宗文 鲁业频 杨汉生

（巢湖学院机械与电子工程学院，安徽 巢湖 238000）

传统的分形图像编码根据图像内部的跨尺度自相似性，求解压缩仿射变换，完成图像编码，这种来自于自身的编码码本不一定是最佳的，而且编码时间通常较长。根据图像之间存在着相似性，构造一个适应性更强的固定编码码本，其它任何图像分形编码的值域块只在这个固定码本中搜索其最佳匹配块，并且省去等距变换，此外，解码也无需迭代。实验结果表明，在图像质量略有下降情况下，该算法较基本分形图像编码算法显著地提高了编码和解码的速度，而且算法简单，容易实现。如果对这种固定码本加以更好的适应性改造，将会进一步提高解码图像的质量。

分形；固定码本；快速分形编码；相似性；最佳匹配；非迭代

引言

分形图像编码是比较有前途的第二代图像编码技术，其较高的率失真性能、分辨率无关性、迭代解码的新颖思想正受到人们广泛关注。1988年M.F.Barnsley提出了迭代函数系统［1］（IFS），并应用到图像压缩编码中，取得了极高的压缩比，但该方法需要人机交互，对操作者要求较高，无法实用。1990年A.E. Jacquin提出了基于分块的分形图像压缩方案［2］，在方案中，首先将图像划分为许多互不重叠的值域块，然后对每个值域块，按照仿射变换在原始图像的紧缩图像中寻找最相似的部分，这些操作可由计算机自动完成，它为分形图像编码带来了一次大的飞跃。然而分形图像编码与其他编码技术（DCT编码，小波编码）［3-6］相比在编码阶段耗费时间过长，因此近二十年来，许多学者发表了大量的论文，主要是讨论如何加快编码速度［7-13］。但在所有这些文献中，他们使用的编码码本（定义域块集）都是来自于待编码图像本身，因为分形编码主要思想是基于图像的自相似性以及不动点定理、拼贴定理的数学原理［1，2］，不动点定理能够保证解码图像稳定，拼贴定理给出了解码图像与原图像误差的上限。但是我们有理由相信，跨图像的相似性也是普遍存在的，也就是说我们可以设计一个不依赖于待编码图像的码本，让待编码图像的值域块在这样的码本内寻找它的最佳匹配块，当然这种固定码本应有足够的适应性，以适应不同的图像，本文正是基于这种想法做了一些探讨与实验。为了更好地阐述这种固定码本分形编码的做法，有必要首先简要介绍基本分形编码的数学原理和算法。

1 基本分形编码的数学原理

1.1 压缩映射定理

令ω：X→X为度量空间（X，d）上的变换，若存在一个常数0≤s＜1，使得

则称ω为压缩映射，s为压缩因子。

1.2 迭代函数系统

一个迭代函数系统（IFS）包括一个完备度量空间，以及一系列定义于该空间上的压缩映射ωn：X→X，压缩因子分别为sn，n=1，2…，N。定义分形空间（H（X），dH）上的变换：W：H（X）→H（X）

1.3 拼贴定理

在分形空间（H（X），dH）中，设W：H（X）→H（X）是其上的压缩因子为s的压缩映射，A是该压缩映射的不动点（吸引子），则∀C∈H（X），有

因为在编码阶段，已经求出W使得待编码图像C与W（C）非常靠近，所以根据拼贴定理，迭代解码的不动点图像A应与原图像C接近。

2 基本分形编码算法［2］［14］

2.1 编码

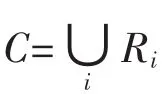
2.2 解码

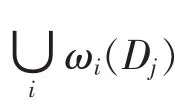
3 固定码本编码算法

3.1 固定码本的构造

图像的跨尺度相似性不仅存在于图像内部，也存在于图像之间，为了兼顾各种图像的可能边缘结构和灰度变化信息，如果能构造一个包含了各种图像的边缘结构和灰度变化信息的图像模板，就能够对任意图像做到最佳匹配，但实际上这种图像模板很难构造，即使图像内部也难以存在跨尺度下的完全相似。需要强调的是图像块不能匹配自身，这样做毫无意义。我们简单地构造了一幅图像模板，如图1所示，该图看起来只是简单的几个线条，但是它包含了很多边缘结构，如各种弧形边缘、直角形边缘，以及它们的等距变换和亮度变换，包含等距变换的好处是在搜索最佳匹配时可以省掉等距变换，从而加快编码速度。另外还要考虑到各种图像灰度变化的比例不同，一个可行做法是构造图像模板时，在多个不同部分使得灰度交错变化，这样可以更加准确地实现灰度上的匹配。对于任何一个待编码图像，只要做到子块形状和灰度上足够匹配，就会得到较高的解码图像质量。构造图1所示的图像模板充分地考虑了这些特点。

图1 生成固定码本的图像模板

3.2 算法分析

图像编码：

第一步：将大小为N×N的原始图像C分割为互不重叠的大小为B×B的值域块Ri，即

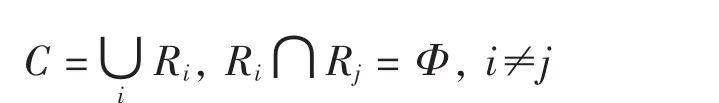
第二步：用B×B的截取窗以δ为滑动步长从大小为N/2×N/2的图1模板中，截取定义域块Dj，并构成固定码本

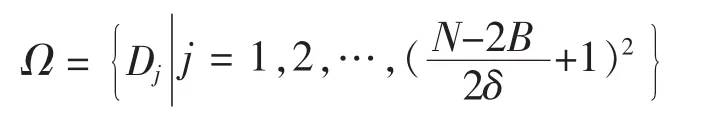
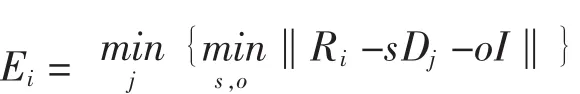
图像解码：

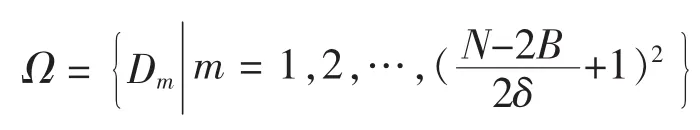
该算法除了码本不是来自待编码图像外还有几个重要特点：1）编码阶段无需等距变换，这样可加快编码速度；2）对比度因子s无需限定为，这样可提高解码图像质量；3）解码阶段无需迭代，这样可加快解码速度；4）编解码的定义域块均来自同一固定码本，且该固定码本无需传输，这样可提高传输效率。

4 实验结果分析

我们首先测试基本分形算法和固定码本算法对几幅不同测试图像编码时所产生的匹配误差。实验中测试图像都是512×512灰度图像，R块都是8×8分割，滑动步长δ都是16，结果如图2所示。

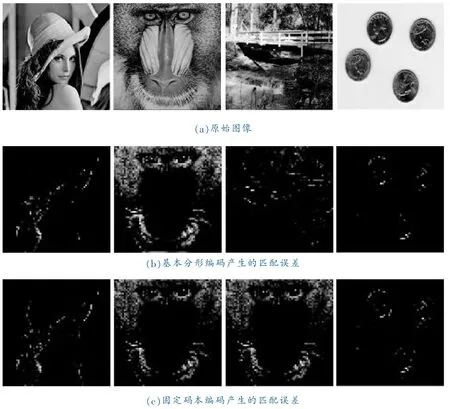
图2 不同编码方式产生的匹配误差比较

从图2中可以看出，不管是选择哪种码本，匹配的误差主要还是图像的边缘和细节部分；图（b）是从图像本身产生的码本中搜索匹配块产生的误差，图（c）都是从固定码本中搜索匹配块产生的误差，可以看出两种算法产生的匹配误差主观质量相近。

表1进一步对两种不同编码算法的性能进行了比较，仿真的平台是：Windows操作系统、3.2GHz的CPU主频、3GB物理内存，所有算法由MATLAB7.9软件实现。

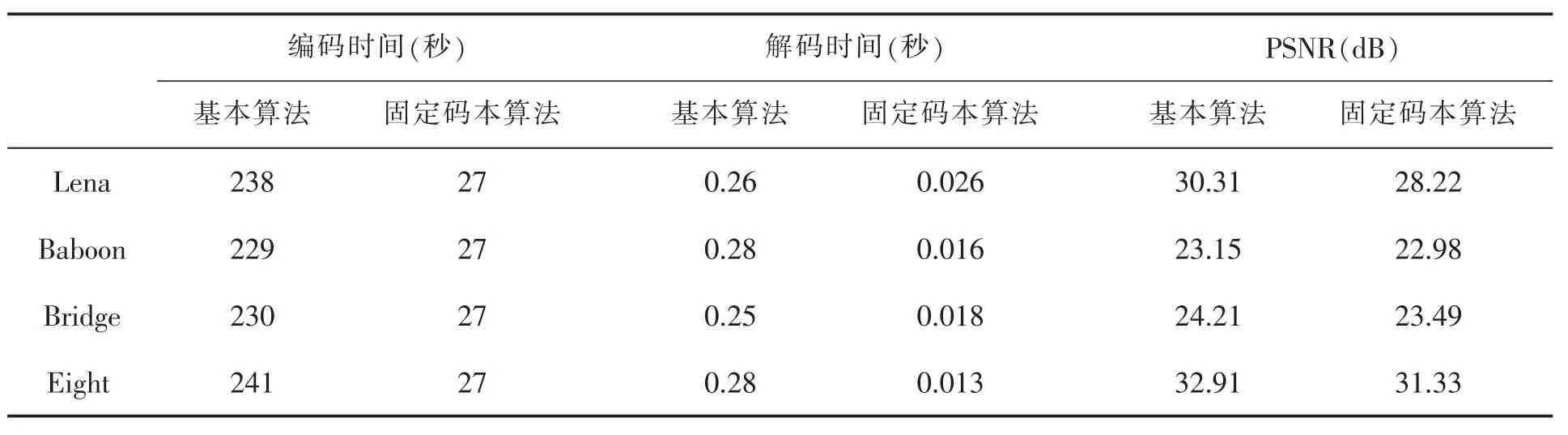
表1 两种不同算法的性能比较

从表1中可以看出，固定码本算法的编码速度较基本算法平均加快8.7倍，解码速度平均加快14.7倍，峰值信噪比PSNR平均下降1.14dB。另外，固定码本算法由于没有进行等距变换，较基本分形算法的分形码少了一个等距变换参数t，只有三种参数，所以压缩比较基本算法提高25%。值得一提的是，固定码本算法已经不属于严格意义上的分形图像编码了，对比度因子s没有做的限制，解码时也没有迭代解码，实际上该算法没有求解压缩映射，从而不动点定理、拼贴定理也就不复存在。因为没有了基本分形算法中的拼贴定理（式（5）所示）的保证，固定码本算法是不可进行迭代解码的。图3（a）是固定码本算法通过迭代10次得到的Lena图像，图3（b）是该算法没有迭代解码得到的Lena图像。

图3 迭代解码对固定码本算法的影响

5 总结

本文根据图像相似性的普遍存在性，对基本分形的码本构成进行了改进，构造了一个不依赖于待编码图像的固定码本，作为任何图像分形编码的共同码本。实验结果表明该固定码本算法较基本分形编码算法，在略微牺牲了一点图像质量（1.14dB）的代价下，较为显著地提高了编码速度（8.7倍）和解码速度（14.7倍），而且该算法简单，特别是解码无需迭代，因此具有一定的应用价值。

本文构造的码本显然不是最好的，固定码本算法的难点在于怎样更好地构造一个不依赖于任何待编码图像的固定码本，即如何构造一个最具适应性的码本，目前这方面还缺少系统的理论分析和相关结论，只能通过实验不断地改进，所以这些问题都有待进一步的研究。

［1］Barnsley M.F..Fractal everywhere［M］.Academic Press，1988：375-377.

［2］A.E.Jacquin.Image coding based on a fractal theory of iterated contractive image transformations［J］.IEEE Trans.Image Process，1992，（1）：18-30.

［3］Yao Zhao，Baozong Yuan.Image compression using fractals and discrete cosine transform［J］.Electronics Letters，1994，（6）：474-475.

［4］K.U.Barthel，et al.A new image coding technique unifying fractal and transform coding［J］.Proc.of ICIP，1994，（3）.

［5］Alex Pentland，Bradley Horowitz.A practical approach to fractal-based image compression［J］.IEEE Computer society，Mar.，1991：176-185.

［6］G.M.Davis.A wavelet-based analysis of fractal image compression［J］.IEEE Transaction on Image Processing，February，1988，（2）：141-154.

［7］Fisher Y.，Jacobs E.W.，Boss R.D..Image compression：a study of the iterated transform method［J］.Signal Processing，1992，（3）：251-263.

［8］Hurtgen B.，Stiller C..Fast hierarchical codebook search for fractal coding of still image［C］.Berlin，Germany，1993：397-408.

［9］Martio P.，Michele N..Speed up in fractal image coding：comparison of methods［J］.IEEE Trans.on Image Processing，2000，（6）：1002-1009.

［10］Y.H.Moon，H.S.Kim and J.H.Kim.A Fast Fractal Decoding Algorithm Based on the Selection of an Initial Image［J］. IEEE Trans.Image Process，2000，（5）：941-945.

［11］C.He，S.X.Yang and X.Y.Huang.Variance-based accelerating scheme for fractal image encoding［J］.IEE Electronics Letters，2004，（2）：115-116.

［12］C.Lai，K.Lam and W.Siu.Improved searching scheme for fractal image coding［J］.IEE Electronics Letters，2002，（25）：1653-2654.

［13］C.Lai，K.Lam and W.Siu.A fast fractal image coding based on kick-out and zero contrast conditions［J］.IEEE Transactions on Image Processing，2003，（11）：1398-1403.

［14］何传江.分形图像编码技术的算法研究［D］.重庆：重庆大学，2004：105-108.

ON THE ALGORITHM OF FRACTAL IMAGE CODING BASED ON FIXED CODEBOOK

YUAN Zong-wen LU Ye-pin YANG Han-sheng
（College of Mechanical&Electronic Engineering，Chaohu College，Chaohu Anhui 238000）

The traditional fractal image coding is based on the self-similarity across different scales of the image inside，solves the compression affine transformation and completes the image coding.The codebook from the image itself is not necessarily the best，and the encoding time is usually longer.According to the existence of similarities between the images，we construct an adaptable codebook in which the best matching block can only be searched for by the range block of any image fractal coding，and isometric transformation is omitted.In addition，there is no need to iterate the decoded image.Experimental results show that in the case of a slight decrease in image quality，the algorithm has better performance than basic fractal image coding and improves the encoding and decoding speed，and the algorithm is simple and easy to implement.If the fixed codebook improves through a better adaptation，it will enhance the quality of the decoded image.

fractal；fixed codebook；fast fractal coding；similarities；best matching；non-iterative

陈小举

TP391

A

1672-2868（2015）03-0078-06

2015-02-05

安徽省高等学校自然科学研究项目基金支持（项目编号：KJ2011B103）

袁宗文（1978-），男，安徽含山人。巢湖学院，讲师，硕士。研究方向：多媒体信息处理、数字电视技术。