数学原理教学探究——以高中三角函数诱导公式为例

崔娅兰

（贵州师范大学 贵州贵阳 550000）

数学原理教学探究——以高中三角函数诱导公式为例

崔娅兰

（贵州师范大学 贵州贵阳 550000）

原理的教学是中学数学教学的重要内容之一，其教学的好坏直接影响着学生知识技能的掌握与能力的培养。高中阶段三角函数诱导公式的教学中，教师如何转化教学方法，利用诱导公式的推导过程，总结方法，为学生化繁为简，化难为易是原理教学的重点。

原理教学 三角函数 诱导公式

数学教学一般分为概念形成、概念同化和原理教学。数学原理教学指对数学中的性质、公式、公理和定理等的教学。

一、探索原理本质，还原思维过程

三角函数诱导公式教学属于原理的教学。原理的学习不仅要学会描述原理的符号信息，即记住相关公式，还要揭示证明思路的探究过程。

在诱导公式的教学中，教师应将讲课的重点放在揭示定理结论的过程及其证明思路的探索过程上。首先，公式一揭示了α与之间的三角函数关系。通过观察终边，可以发现这类三角函数的终边相同，那么三角函数值相同。公式二是探究α与α+π之间的三角函数关系，由单位圆中三角函数定义可得出公式二。同理，可以得出公式三、公式四的推导过程。此外，也可以将α转化为-α由公式二、公式三直接推导出公式四。利用单位圆中的三角函数还可以得出之间的关系式，即公式五，再将α转化为-α由公式五得出公式六。利用前面公式也可以得出α与之间的三角函数关系式。通过不同的推导方式，可以展示不同的数学思维方法。

二、总结原理特点，重视公式理解

将对象与结果简单化与符号化是数学思维的重要特征，也是数学家所追求的目标之一，于是就形成了公式，公式教学包含了公式的推导、理解、记忆和运用。

高中三角函数诱导公式的教学，主要是通过几何上的关系推导出函数代数上的关系，通过发现α与在直角坐标系中的终边的对称关系，也可以利用三角函数定义和单位圆，进而推导出三角函数之间的关系。这样的教学设计可以培养学生数形结合的思想，也可以给学生讲清楚公式的来源，使其理解并能够证明诱导公式。但是，当六大类公式一起进行化简证明相关三角函数题时，就需要强化公式的记忆。同样，如果让学生课后再将六大类公式包含十八个公式进行强化记忆，那么，在公式的运用时同样很容易出错。例如：在化简时，第一步将化为；第二步化为最后再化成。学生在理解第一步时是没有什么障碍的，但是第二步去掉π，学生就需要回忆公式，容易出错，最后一步化简时，又要运用到公式六，同时，化简时还会遇到化简的情况。这无疑又增加了学生的学习负担。如何将公式化难为易？

教学中，我们需要让学生将机械记忆转化为理解记忆，而对于三角函数诱导公式可以在推导过程中帮助学生理解记忆，但是，由于公式繁多，推导过程较为复杂，这时就需要变通记忆，即将所学的公式转化为生活语或是口诀。口诀来源于公式本身，所以，此时教师应该引导学生善于观察，总结公式特征，让学生自己发现公式：如果涉及的公式中，k为奇数时，函数名称需改变（即sinα），k为偶数时，函数名称不改变（即cosα）。函数值的符号就要看所在的象限符号。此时即可变通记忆为：“奇变偶不变，符号看象限”。

三、注重知识联系，解决应用困难

原理学习同概念学习相似，都是新旧知识相互作用形成新的知识认知结构的过程。所以，要想更好地学习原理，就应当让学生的认知结构中具备与新的原理相关的数学知识。教学过程中，教师可以引导学生回忆已有相关知识，建立新旧知识的联系，帮助学生找到解决问题的方法。

三角函数诱导公式中，即便有了“奇变偶不变，符号看象限”的口诀，但是在确定符号时，学生往往会困惑，因为任意角的化简会涉及到，此时的化简很容易出错，那么，有没有方法可以更好的解决问题呢？

数学原理的教学不仅要学生理解和掌握数学的性质、法则、公式等，而且要使学生理解这些原理所蕴涵的数学方法，并在学习和应用这些原理的过程中发展自己的数学认识结构，形成自己的数学思想方法。利用数形结合的思想，可以将诱导公式的应用简化，可以快速并准确地进行求值计算和化简证明。如图3.1所示：

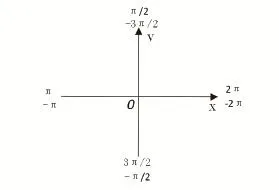
由图3.1可知，首先将α看作第一象限内的角（因为第一象限内的角的任意三角函数值都为正，无负号）。sin（2π-α）中2π为的偶数倍，函数同名，2π的终边在x轴的正半轴，如果减α，那么应该顺时针旋转α度，则终边在第四象限，第四象限的正弦值为负，则化简为-sinα；的奇数倍，函数名称改变，终边在y轴正半轴，如果再加α，则逆时针旋转α度，终边在第二象限，第二象限内余弦函数值为负，则化简为-sinα。同理，运用此方法快速准确地化简其它三角函数值，最终结果为-sinα。运用此方法学生无需记任何公式，则彻底解决了三角函数诱导公式的难理解，难记忆，难运用问题。

综上所述，原理的教学要注重原理的探索体验过程，重视学生思维过程和数学思想方法。原理的记忆需要以理解记忆为主，如果原理的推导过程过于繁杂，那么就需要变通记忆，在理解与变通的基础上联系已知，从更高的角度深刻理解数学本质。