自行火炮自动直瞄控制方法研究
2015-11-11张卫民梁建奇马红卫王彤武智晖
张卫民,梁建奇,马红卫,王彤,武智晖
(1.中国兵器工业导航与控制技术研究所,北京100089;2.中国兵器科学研究院,北京100089)
自行火炮自动直瞄控制方法研究
张卫民1,梁建奇1,马红卫1,王彤1,武智晖2
(1.中国兵器工业导航与控制技术研究所,北京100089;2.中国兵器科学研究院,北京100089)
针对自行间瞄火炮现状,提出在不增加火控系统硬件配置的前提下实现对固定目标和运动目标的自动直瞄控制方法,研究了控制模型和弹道快速解算方法,分析了瞄准误差和系统反应时间。结果表明,此方法可显著提高火炮直瞄时的快速反应能力和射击精度以及武器系统的自动化操作水平。
兵器科学与技术;自行火炮;自动控制;直瞄射击;快速反应
0 引言
自行间瞄火炮以间瞄射击方式为主,其直瞄射击方式大多是在与敌遭遇时应急使用,因此提高武器系统在直瞄射击时的快速反应能力非常重要。针对此问题,本文提出一种自动直瞄控制方法,利用自行火炮火控系统原有的硬件条件,通过控制软件实现对固定目标和运动目标的自动直瞄射击,将直瞄射击时的操作步骤简化为瞄准-测距-射击,应急情况下系统的反应时间为2 s左右(从发射激光测距到自动瞄准后开炮),可显著提高武器系统在直瞄射击时的快速反应能力和自动化水平。该方法与坦克火控系统的原理基本相同,区别是测距后“系统自动瞄准”,而坦克火控系统(除自动跟踪式火控系统之外)是击发前一直人工瞄准[1-2]。此外,该方法基于停止间瞄准射击(间瞄火炮目前只能在停止间瞄准射击),而坦克可以在行进间瞄准射击。
本文提出的自动直瞄控制方法,不受传统意义的直瞄射击距离限制,适用于激光测距范围内的任何可通视目标。
1 自动直瞄控制模型研究
1.1自动直瞄控制方案简述
不失一般性,假设自行火炮火控系统已配置火炮高低、炮塔方位、炮塔纵/横倾姿态等传感器,具有弹道解算和自动操瞄调炮等功能,并配置直瞄镜和激光测距机,则本方案不增加任何设备,只要求激光测距机和火控计算机有通信功能。
对固定目标射击时,瞄准手手动(半自动)控制火炮,用直瞄镜瞄准目标后激光测距,测距信息发送到火控计算机。火控计算机计算表尺修正量和方位修正量,然后控制火炮自动瞄准到位。瞄准手在激光测距后即可按下击发按钮,当目标进入预置的射击门时,火炮自动击发。
对运动目标射击时,瞄准手通过半自动操纵台控制火炮,用直瞄镜瞄准目标,按下激光发射按钮,平稳跟踪目标2~4 s后松开,激光测距信息发送到火控计算机。火控计算机根据传感器的数据计算目标运动角速度和提前量以及表尺修正量,然后自动调炮跟踪瞄准目标。瞄准手在激光测距后即可按下击发按钮,当目标进入预置的射击门时,火炮自动击发。
1.2坐标系定义及转换关系
1.2.1有关定义[3-4]
定义1:炮塔坐标系Oxyz——设炮塔回转中心为坐标原点O,x轴为火炮轴线在炮塔回转平面的投影,向前为正;z轴沿炮塔回转平面法线向上,y轴向右,Oxyz构成左手坐标系。
定义2:炮塔纵倾角θ——炮塔坐标系x轴与水平面之夹角,前倾为正。
定义3:纵倾平面——炮塔坐标系y轴水平,x轴与水平面之夹角为θ时的炮塔回转平面。
定义4:炮塔横倾角γ——炮塔坐标系y轴与纵倾平面之夹角,沿火炮轴线向前看,右倾为正。
定义5:炮塔水平坐标系Ox0y0z0——当θ=γ= 0 mil时的炮塔坐标系。
定义6:炮塔方位角β——炮塔座圈旋转的角度,火炮轴线与车体同向时为0 mil.
1.2.2坐标系的转换关系
定义转换矩阵如下:
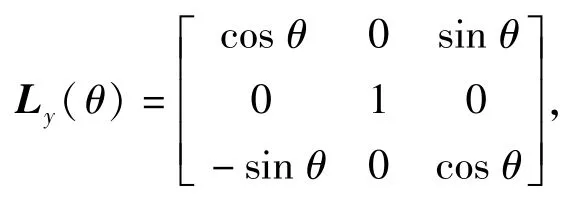

设空间一点在炮塔坐标系和炮塔水平坐标系下的坐标分别为(x,y,z)和(x0,y0,z0),则根据上述定义,可得到如下转换关系:

1.3对固定目标自动直瞄射击数学模型
设目标距离为D,测距时(瞄准目标时)火炮在炮塔坐标系下的高低角为ε,则此时火炮轴线在炮塔坐标系下的单位向量为

又设测距时炮塔横倾角和纵倾角分别为γ和θ,则可由(2)式求得火炮在炮塔水平坐标系下的单位向量(x0,y0,z0),进而求得火炮在炮塔水平坐标系下的方位角β0和高低角ε0:
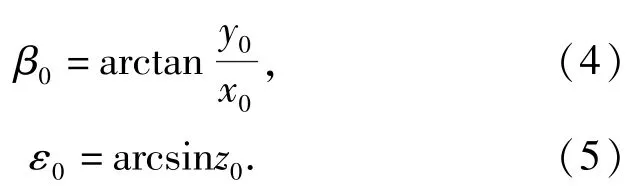
设炮目高程差为Δh,则有

火控计算机根据目标距离、炮目高程差、气象参数、弹药条件等,计算直瞄射击时炮塔水平坐标系下的弹道修正量Δβ0、Δε0,进而可得炮塔水平坐标系下的直瞄理想射击诸元
设β*、ε*为炮塔坐标系下直瞄理想射击诸元,则参照(3)式有
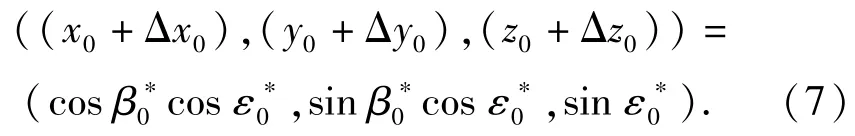
再由(1)式可得((x+Δx),(y+Δy),(z+ Δz)),进而有

设Δβ、Δε为转换到炮塔坐标系的弹道修正量,则有

火控计算机控制炮塔旋转Δβ角,同时控制火炮高低角在炮塔坐标系下旋转Δε角,即完成自动瞄准。
1.4对运动目标直瞄射击数学模型
与坦克相比,自行间瞄火炮无论传感器的配置还是随动系统的性能均有很大差距,因此对运动目标直瞄射击的数学模型也只能以此为基础建立,不能要求过高。
对运动目标直瞄射击时,假设目标运动过程中距离不变,运动角速度不变[1]。
设tp为瞄准手瞄准目标按下激光测距按钮时刻,tr为瞄准手抬起激光测距按钮时刻(即测距时刻),βi、εi(i=p,r)分别为对应时刻的炮塔方位角和火炮在炮塔坐标系下的高低角;又设在tr时刻炮塔坐标系下目标运动角速度在方位向和高低向分别为ωβ和ωε,则可由下式得其估计值:
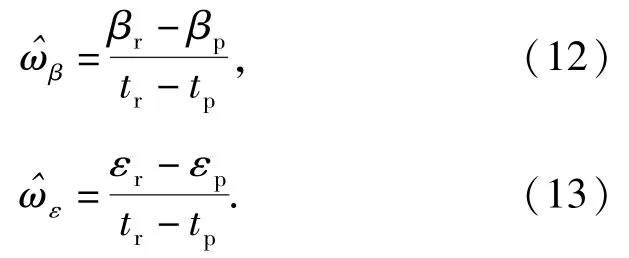
根据tr时刻的有关参数,参照(3)式~(11)式,可得炮塔坐标系下的弹道修正量Δβ、Δε.
又设Δt为弹丸飞行时间,β*(t)、ε*(t)分别为未来t(t>tr)时刻炮塔方位角理想值和炮塔坐标系下高低角理想值,则有
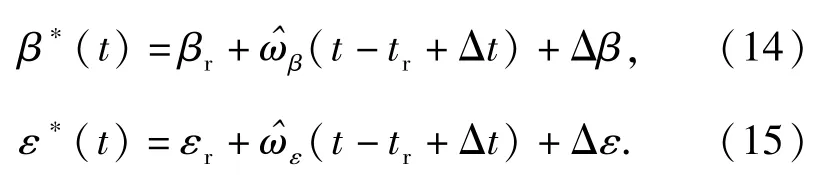
火控计算机控制火炮按诸元β*(t)、ε*(t)自动瞄准即可。由于β*(t)、ε*(t)是随目标运动而等速变化的,因此火炮的随动系统应设计为二型或二型以上系统,以便对速度信号有良好的跟踪特性。
1.5快速直瞄弹道解算方法
由于弹道解算时间直接影响到自动直瞄的反应时间,因此针对直瞄射击射程较近的特点,可采用更快速的射表拟合方法计算弹道。相对标准弹道条件,拟合时主要考虑以下因素的影响:1)气温变化对射程的影响;2)药温变化对射程的影响;3)空气密度对射程的影响;4)初速变化对射程的影响;5)纵风对射程的影响;6)弹重变化对射程的影响;7)炮目高差对射程的影响;8)横风对方向的影响;9)偏流对方向的影响等。
根据射表在相关射程以内的有关数据,采用二次多项式分别拟合以上诸因素在标准条件下对应的距离修正量、射角修正量或方向修正量。
设d为激光测距机测量的目标实际距离,d0为等价于标准条件下的目标距离,ΔdΔTa、ΔdΔTc、ΔdΔρ、ΔdΔv0、Δdw、ΔdΔW分别表示由拟合公式求得的气温偏差、药温偏差、空气密度偏差,初速偏差、纵风和弹重偏差等因素所引起的距离修正量(若Δv0>0,则ΔdΔv0<0,以此类推),则有

设标准条件下与射击距离d0对应的射角为α0,弹丸飞行时间为Δt,则可由射表拟合公式求得

同时可由射表拟合公式求得与炮目高程差Δh和距离d0对应的射角修正量Δα:
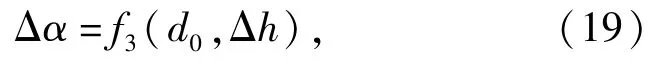
式中:射角修正量Δα是在炮目高低角基础上加的修正量,目标距离较近时可忽略。
最终可得自动直瞄时的射角修正量

设Δβ1、Δβ2分别表示由拟合公式求得的偏流和横风修正量,则自动直瞄时的方向修正量为

(20)式和(21)式中的Δβ0、Δε0即前面讨论中涉及的炮塔水平坐标系下的弹道修正量。
2 自动直瞄瞄准误差分析
2.1对固定目标瞄准误差分析
以自动直瞄方式对固定目标射击时,影响瞄准精度的误差主要为自动瞄准时火炮随动系统的到位误差,其他误差(激光测距误差、弹道解算误差、姿态传感器测量误差等)由于仅对弹道修正量的计算产生影响,与之相比可忽略。
火炮随动系统到位误差的均方差一般为0.3 mil,反应在3 000 m立靶上的位置偏差小于1 m(均方差),可以满足一般情况下的作战需求。若通过改善随动系统性能和减小到位门限值(射击门),此误差还可能进一步减小。
2.2对运动目标瞄准误差分析
对运动目标射击时,自动直瞄方式的瞄准误差由两部分组成:
1)目标运动角速度测量误差。由(14)式、(15)式可知,目标运动角速度的测量不但关系到提前量的计算精度,还影响到火炮对目标自动跟踪瞄准的精度。此项误差取决于操作者的经验。
2)火炮随动系统自动跟踪误差。根据目标运动假设,目标相对火炮等角速度运动,对于火炮随动系统而言相当于跟踪一个斜坡输入信号。此时,若随动系统设计为二型系统,则对斜坡输入信号没有稳态跟踪误差,因此随动系统对控制信号的跟踪误差取决于射击门的设置。
此外,由(14)式、(15)式可知,若目标运动角速度有测量误差,则自动跟踪瞄准的时间越长,瞄准的误差越大。因此自动直瞄对运动目标射击的关键有:一是目标运动角速度测量误差尽量小;二是自动跟踪瞄准的时间应尽量短,即系统响应速度应足够快。
2.3与手动直瞄方式的比较
传统的手动直瞄方式由于没有考虑除距离之外其他因素对弹道的影响和车体倾斜修正,因此目标距离越远,瞄准误差越大。特别是在目标距离超出直瞄镜表尺范围时(激光测距范围一般大于5 km,而表尺范围一般为3 km左右),将无法瞄准。
对于目标运动,手动直瞄时只能凭经验估算提前量,无法保证瞄准精度。
2.4与自动间瞄方式的比较
对于激光测距范围内的远距离(如5~10 km)可通视目标,若采用自动直瞄方式射击,则比采用自动间瞄方式射击时减少了火炮定位、定向、目标坐标测量等多项误差,瞄准精度将显著提高。
3 自动直瞄系统反应时间分析及仿真
3.1系统反应时间分析
传统手动方式直瞄射击时的操作步骤为瞄准-测距-装表-再瞄准-射击,而自动直瞄时的操作步骤简化为瞄准-测距-射击,快速反应能力显著提高。
自动直瞄时的系统反应时间定义为从瞄准目标激光测距(发射激光)开始,到火炮自动瞄准到位(可立即击发)为止的时间,包括火控解算时间(含弹道解算时间)和随动系统调炮瞄准时间。若采用快速弹道解算方法,经计算机仿真验证,火控解算时间为毫秒级,可忽略。因此,自动直瞄时的系统反应时间主要取决于随动系统自动调炮瞄准到位的过渡过程时间。
由前面的分析可知,自动调炮瞄准时火炮的转动量不大,同时由于火炮进入射击门即可击发,不要求火炮稳定在射击门之内,因此可进一步缩短瞄准到位的时间。根据上述条件,目前国内自行火炮火控系统一般情况下均可在2 s左右完成自动瞄准。
3.2火炮随动系统计算机仿真
由于火炮俯仰方向转动惯量远小于方位方向,更易于控制,因此以方位方向为例,根据某自行榴弹炮的有关参数,建立火炮随动系统仿真模型,系统框图如图1所示。

图1 火炮方位随动系统示意图Fig.1 Schematic diagram of gun azimuth servo system
3.2.1对固定目标自动直瞄仿真
对固定目标自动直瞄时,随动系统PID控制器采用原设计参数,不做改动。
设由(10)式求得炮塔坐标系下的方位方向弹道修正量为0.01 rad(约10 mil),即方位随动系统的输入为阶跃信号r(t)=0.01(t>0).经仿真可得方位随动系统的阶跃响应,如图2所示。

图2 方位随动系统阶跃响应Fig.2 Step response of azimuth servo system
由图2可见,系统反应时间小于2 s,稳态瞄准误差可忽略。
3.2.2对运动目标自动直瞄仿真
为了消除稳态速度跟踪误差,对运动目标自动直瞄时随动系统采用重新设计的PID控制器,其中增加了积分环节,使随动系统由一型系统变为二型系统,并适当选取控制器参数。
不失一般性,设目标距离1 000 m,方位方向目标运动角速度为10 mrad/s,又由射表知1 000 m时弹丸飞行时间Δt=1.5 s,因此与弹丸飞行时间对应的方位提前量为15 mrad.由(14)式易见,此时方位随动系统的输入信号为斜率10 mrad/s的斜坡信号,并在t=tr时刻(本例中取tr=4 s)叠加一个幅值为15 mrad的阶跃信号。经仿真求得随动系统对上述斜坡信号的响应,如图3所示。

图3 方位随动系统对斜坡输入信号的响应Fig.3 Response of azimuth servo system on ramp input signal
由图3可见,系统反应时间小于2 s,随动系统稳态跟踪误差可忽略。
4 结论
本文提出了一种用于自行间瞄火炮的自动直瞄控制方法,通过控制软件实现对目标的自动直瞄瞄准。该方法有如下特点:
1)操作简便,自动化程度高。操作者只需对目标瞄准一次,测距后即可按击发按钮,等待火炮自动瞄准到位后击发。
2)快速反应能力强。一般情况下,从瞄准测距到火炮击发只需2 s左右。
3)瞄准精度高。与手动直瞄方式相比,由于充分利用了传感器信息、气象信息、火控系统的计算功能和自动调炮功能,瞄准精度显著提高。与自动间瞄方式相比,由于减少了误差环节,瞄准精度也显著提高。
4)适用范围广。不受传统意义的直瞄射击距离限制,适用于激光测距范围内的任何可通视目标。
本文提出的自动直瞄对固定目标的射击方法,已在某自行火炮上进行了实弹射击试验验证,试验结果与上述分析和仿真结果一致。
(
)
[1]周启煌,单东升.坦克火力控制系统[M].北京:国防工业出版社,1997. ZHOU Qi-huang,SHAN Dong-sheng.Tank fire control system[M]. Beijing:National Defense Industry Press,1997.(in Chinese)
[2]朱竞夫,赵碧君,王钦钊.现代坦克火控系统[M].北京:国防工业出版社,2003. ZHU Jing-fu,ZHAO Bi-jun.WANG Qin-zhao.Modern tank fire control system[M].Beijing:National Defense Industry Press,2003.(in Chinese)
[3]陶化成.一个新的压制兵器自动操瞄控制方案[J].兵工学报,1997,18(1):9-14. TAO Hua-cheng.A new suppression weapon auto-aiming control scheme[J].Acta Armamentarii,1997,18(1):9-14.(in Chinese)
[4]陈明俊,李长红,杨燕.武器伺服系统工程实践[M].北京:国防工业出版社,2013:261-281. CHEN Ming-jun,LI Chang-hong,YANG Yan.Weapons servo system engineering practice[M].Beijing:National Defense Industry Press,2013:261-281.(in Chinese)
An Automatic Direct Aiming Control Method of Self-propelled Artillery
ZHANG Wei-min1,LIANG Jian-qi1,MA Hong-wei1,WANG Tong1,WU Zhi-hui2
(1.Navigation and Control Technology Institute,China North Industries Group Corporation,Beijing 100089,China;2.Ordnance Science and Research Academy of China,Beijing 100089,China)
An automatic direct aiming control method is proposed for self-propelled indirect aiming artillery.The proposed method can be used to make a self-propelled artillery directly aim at the fixed and moving targets without the addition of any hardware configuration of fire control system.The control model and the rapid calculation method of trajectory are studied.The aiming error and system response time are analyzed.The method can significantly improve the rapid reaction ability and firing accuracy of artillery and the automation level of weapon system.
ordnance science and technology;self-propelled artillery;automatic control;direct aiming fire;rapid reaction
E924
A
1000-1093(2015)01-0182-05
10.3969/j.issn.1000-1093.2015.01.026
2014-02-13
张卫民(1955—),男,研究员。E-mail:zwm602@263.net
