OFDM系统中子信道联合预编码技术的信号检测算法研究

蒋海云等

摘 要： 正交频分复用技术将多径衰落信道划分为多个相对平坦的子信道，使得接收机在信道估计等恢复技术上复杂度大大降低。OFDM系统采用子信道联合预编码技术能有效解决由于成片子载波衰落引起的数据丢失问题。由于独立信道的线性预编码技术在发送端不需要信道反馈信息，因此降低了发送设备复杂度，减少了系统延时，该编码方案适用于从用户端到基站的数据传输。通过理论分析推导了当系统采用独立信道的线性预编码技术时，接收端不能采用迫零均衡（ZF）的线性检测算法，实验仿真表明，当采用迫零均衡检测算法时，当且仅当预编码矩阵为酉矩阵时系统能达到未经预编码系统的性能。

关键词： OFDM系统； 子信道联合预编码； 迫零均衡检测算法； 星座调制信息

中图分类号： TN92?34 文献标识码： A 文章编号： 1004?373X（2015）21?0046?03

Research on signal detection algorithm of sub?channel joint precoding technology in OFDM system

JIANG Haiyun， XIONG Chunlin， WEI Jibo

（School of Electronic Science and Engineering， National University of Defense Technology， Changsha 410000， China）

Abstract： The multipath fading channel is divided into multiple relatively flat sub?channels by OFDM， which makes the receiver′s complexity in channel estimation reduced greatly. OFDM system with sub?channel joint precoding technology can effectively solve the problem of data loss caused by numerous carrier wave fading. Since the linear precoding technology of independent channel doesn′t need feedback information of the channel in sending end， which can reduce the complexity of the transmitting device and system delay， this precoding scheme is suitable for data transmission from the client to the base station. In this paper， a conclusion that the linear detection algorithm of zero forcing equilibrium can′t be adopted for receiving end when the linear precoding technology of independent channel is applied by the system is derived according to the theoretical analysis. The experimental simulation results show that the system can achieve the performance without precoding when the precoding matrix is unitary matrix and zero forcing equilibrium detection algorithm is adopted.

Keywords： OFDM system； sub?channel joint precoding； zero forcing equilibrium detection algorithm； constellation modulation information

0 引 言

无线通信技术的迅猛发展极大地改变了人们生产生活方式，正交频分复用技术[1]（OFDM）作为无线通信的关键技术之一，在很大程度上降低了通信系统的复杂度。在多用户通信过程中，从用户端到基站的上行链路数据传输要求用户设备尽可能简化。在OFDM系统中，使用子信道联合预编码技术[2?4]能带来性能上的提升。独立信道的线性预编码[5?6]是一类重要的预编码方案，在发送端使用发送数据符号的统计特性设计预编码矩阵，不需要已知信道信息，因此无需信道反馈，降低了发送端设备的复杂度，减少了传输延时。因此独立信道的预编码方案适用于用户端到基站的数据传输。

1 独立信道的线性预编码技术采用迫零检测算

法的性能分析

带预编码的OFDM系统简化框图[7]如图1所示。

图1在数学上可建模[7]为：

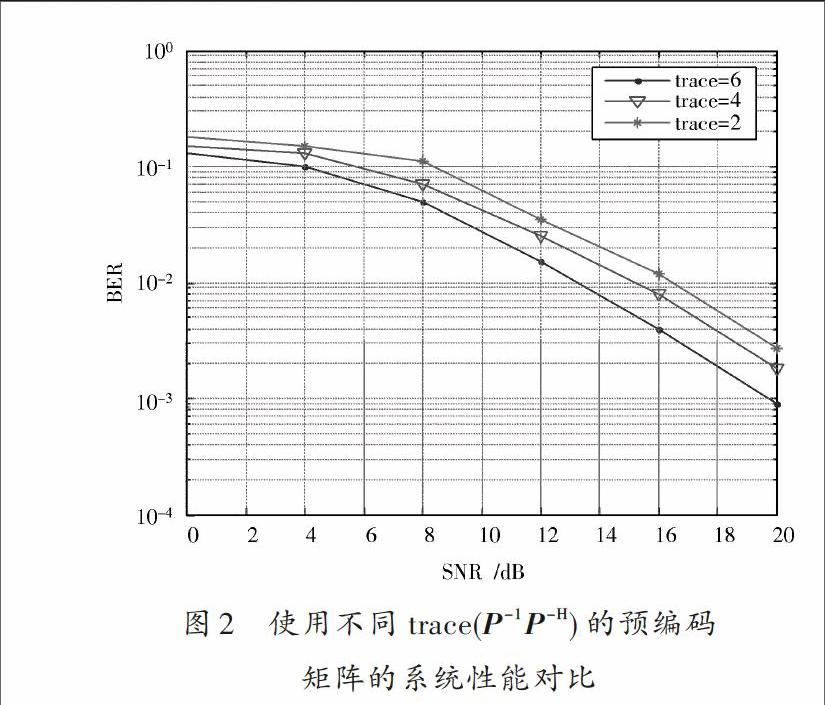
矩阵的系统性能对比

3 结 语

本文从理论和实验仿真两方面分析证明了独立信道的预编码技术不适合采用迫零均衡检测算法。文献[14]从最大化最小子载波信噪比准则出发对独立信道的预编码技术进行了研究，文献[7，9?10]从获得分集增益和编码增益角度出发设计出了独立信道的预编码矩阵，仿真结果表明，当接收端采用最大似然检测（ML）算法或球状译码（SD）等多符号联合检测算法时，文献[7]和文献[14]提出的预编码方案较未预编码方案性能上有较大提升。因此，当采用多符号联合检测算法时，独立信道的预编码技术对于提升OFDM系统传输性能有重要的意义。

参考文献

[1] PROAKIS J G. Digital communication [M]. New York： McGraw?Hill， 1995.

[2] MIYAKAWA H， HARASHIMA H. Matched?transmission technique for channels with Inter?symbol interference [J]. IEEE Transactions on Communications， 1972， 20（4）： 774?780.

[3] TOMLISON M. New automatic equalizer employing modulo arithmetic [J]. Electronic Letter， 1971， 7： 138?139.

[4] SAMPATH H， STOICA P， PAULRAJ A. Generalized linear precoder and decoder design for MIMO channels using the weighted MMSE criterion [J]. IEEE Transactions on Communications， 2001， 49（12）： 2198?2206.

[5] LIN Y P， PHOONG S M. Perfect discrete multitone modulation with optimal transceivers [J]. IEEE Transactions on Signal Processing， 2010， 48（6）： 1702?1711.

[6] SCAGLIONE A， GIANNAKIS G B， BARBAROSSA S. Redundant filterbank precoders and equalizers part I： unification and optimal designs [J]. IEEE Transactions on Signal Processing， 1999， 47（7）： 1988?2006.

[7] LIU Zhiqiang， XIN Yan， GIANNAKIS G B. Linear constellation?precoding for OFDM with maximum multipath diversity and coding gains [J]. IEEE Transactions on Communications， 2003， 51（3）： 294?309.

[8] 孙锴，黄威.MIMO?OFDM无线通信技术及MATLAB实现[M].北京：电子工业出版社，2013.

[9] WANG Z， GIANNAKIS G B. Wireless multicarrier communications： where Fourier meets Shannon [J] IEEE Signal Proces?sing Magazine， 2000， 17（3）： 29?48.

[10] XIN Y， WANG Z D， GIANNAKIS G B. Space?time diversity systems based on linear constellation precoding [J]. IEEE Transactions on Wireless Communication， 2013， 2（2）： 294?309.

[11] 张贤达.矩阵分析与应用[M].北京：清华大学出版社，2004.

[12] AVRIEL M. Nonlinear programming： analysis and methods [M]. New Jersey： Prentice Hall Inc.， 1976.

[13] LUENBERGER D G. Linear and nonlinear programming [M]. 2nd ed. London： Addison?Wesley， 1984.

[14] LIN Yuanpei， PHOONG S M. BER minimized OFDM systems with channel independent precoders [J]. IEEE Transactions on Signal Processing， 2003， 51（9）： 2369?2380.