基于EEMD的共振解调技术在列车轴承故障诊断中的应用
2015-11-09王旭等
王旭等


摘 要: 针对轮对轴承故障信息不易提取的特性,提出了基于EEMD的共振解调方法。首先,采用EEMD方法将原始信号分解为17个IMF分量,计算每个分量的峭度值,选取峭度值大于3的IMF分量相加,合成新的信号;然后,对新的合成信号进行谱峭度分析,得到冲击成分所在的频带,并据此设计带通滤波器对合成信号进行滤波处理;最后,对滤波后的信号进行Hilbert变换和频谱分析,提取冲击成分的频率,并与理论故障频率对比,进行故障诊断。分别对外圈故障、滚动体故障、保持架故障的轴承进行振动试验,并利用此方法对试验结果进行分析,结果表明,该方法能够有效地识别列车轮对轴承的故障信息。
关键词: EEMD; 峭度; 共振解调; 故障诊断
中图分类号: TN911.7?34 文献标识码: A 文章编号: 1004?373X(2015)21?0024?04
Application of EEMD?based resonance demodulation technology in
train bearing fault diagnosis
WANG Xu, PENG Chang, ZHANG Zhenxian
(Technology Center, CSR Qingdao Sifang Co., Ltd., Qingdao 266111, China)
Abstract: For the characteristics of the wheel set bearing fault information is hard to extract, a resonance demodulation method based on ensemble empirical mode decomposition (EEMD) is proposed. The original signal is decomposed into 17 IMF components by EEMD method, and the kurtosis value of each component is calculated. The IMF components whose kurtosis value is greater than 3 are added to composite a new signal. Then the new composite signal is analyzed with spectral kurtosis, and the frequency band where the impacting component is located is obtained. Based on this, a band?pass filter is designed to conduct with filtering processing to the composite signal. Finally the frequency of the impact composition is extracted by Hilbert transformation and spectrum analysis to the filtered signal, and compared with the theoretical fault frequency, then the bearing is proceeded with fault diagnosis. The vibration tests for the bearings of the outer ring fault, rolling body fault, and cage fault were carried on respectively, and the test results are analyzed by using this method. The results show that the method can identify the fault information of the trains′ wheel set bearing effectively.
Keywords: EEMD; kurtosis; resonance demodulation; fault diagnosis
0 引 言
安全性是列车运行的首要条件,随着速度的不断提升,任何一处微小的故障都有可能引起连锁反应,导致整个列车遭受灾难性的毁坏[1]。机械故障诊断技术能够在早期发现机构的故障及原因,并能预报故障的发展趋势,大大降低维护成本,因此,也越来越多地在列车检修中得到应用,其中最常用的是轮对轴承的故障诊断技术。
当轴承某零部件发生故障时,随着轴承的高速旋转,必然会带来周期性的冲击振动。这一冲击信息的能量很微弱,往往被其他信号所淹没,单纯的频谱分析很难将其提取出来。共振解调技术可以将这一低频冲击信号调制到高频的共振频率而远离能量巨大的低频信号,然后再解调处理,提取故障信息[2]。Mathew等结合共振解调技术和AR模型来诊断低速轴承故障[3]。康熊等利用共振解调方法[4]将钢轨焊接接头对车辆?轨道系统的低频周期性冲击特征的分析转换为对其高频共振的分析。王宏超等利用快速kurtogram算法[5]确定共振解调技术中带通滤波器的相关参数,对滚动轴承的故障特征进行了提取。1998年,N.E.Huang等提出了经验模态分解(EMD)的概念[6],自适应地将信号分解成有限个本征模态函数(IMF)之和,每个IMF分量突出了原始信号的局部特征,对每个IMF分量进行分析,可以清晰地得到某单一的故障信息。但是EMD算法并不稳定,且存在模态混叠的问题。2005年,Zhaohua Wu等又提出了集合经验模态分解(EEMD)方法[7],解决了传统EMD方法的模态混叠问题,也更适用于处理复杂的非线性非平稳性信号。
本文对某型列车的轮对轴承进行了振动试验,针对试验数据,采用EEMD的方法将其分解成17个IMF分量,并计算了每一个IMF的峭度值,将具有明显冲击成分的IMF分量相加,合并成新的信号。针对这一合成信号,采用改进的共振解调技术对其进行包络谱分析,提取出了轴承的故障信息。
1 EMD和EEMD方法
经验模态分解(Empirical Mode Decomposition,EMD)是近年来发展起来的一种新的信号处理方法,适用于非线性、非平稳性信号。EMD可以将复杂的振动函数分解成多个本征模态函数(Intrinsic Mode Function,IMF),每个IMF满足以下两个条件:
(1) 函数在整个时间范围内,局部极值点和过零点的数目必须相等,或最多相差一个。
(2) 在任意时刻点,局部最大值的包络和局部最小值的包络必须平均为零。
本征模态函数可由经验模式分解方法进行分解和筛选,具体步骤如下:
(1) 确定信号[xt]所有的局部最大值和局部最小值,利用三次样条插值函数拟合形成原数据的上、下包络线,并计算上下包络线的均值[m1t]。
(2) 求取[xt]与[m1t]的差,可得到一个去掉低频的新数据序列[h1t]。
式中:[μ]和[σ]分别为信号[xt]的均值和标准差;[E]表示取数学期望。轴承无故障运转时,振动信号的幅值分部接近正态分布,峭度指标[β≈3]。随着故障的出现和发展,振动信号中大幅值的概率密度增加,信号分部偏离正态分布,峭度值也随之增大。峭度指标的绝对值越大,说明轴承偏离正常状态越多,故障越严重。
谱峭度是信号频域分析的概念,其基本思路是计算每根谱线的峭度值,从而发现信号中隐藏的不平稳成份,并指出它们所在的频带。滚动轴承的振动信号模型可以表示为:
式中:[ρf]为噪声与实际振动信号的功率谱密度之比。因此,在信噪比很高的频率处,[ρf]无穷小,[Kzf]近似等于[Kxf];在噪声很强的频率处,[ρf]无穷大,[Kzf]近似为零。利用这一功能,可以为共振解调技术中带通滤波器的设计提供参考信息。
3 轮对轴承故障诊断流程
本文综合利用EEMD方法、峭度值、谱峭度以及共振解调技术,对列车轮对轴承故障进行诊断,具体的诊断步骤如下,数据处理的流程如图1所示。
(1) 对采集信号[xt]进行EEMD分解;
(2) 计算各IMF分量的峭度值[βi];
(3) 取[βi>3]的IMF分量相加,得到新的合成信号[xt];
(4) 对[xt]进行谱峭度分析,找出最大谱峭度所对应的频率和带宽,以此设定带通滤波器;
(5) 对[xt]进行带通滤波;
(6) 对滤波后的信号进行Hilbert变换,并进行频谱分析;
(7) 将频谱图的尖峰值与轴承故障频率对比,诊断出故障原因。
图1 故障诊断数据处理流程图
4 轮对轴承振动试验
本文共对7种不同故障的滚动轴承以及一个无故障轴承进行振动试验,发生故障位置包括外圈内表面故障、保持架故障和滚珠故障以及三种故障的混合故障。轮对一侧安装故障轴承,另外一侧安装无故障轴承,试验台及轮对安装位置如图2所示。根据不同的故障信息,设定不同的轮对运行速度等级,最低速度为[30 kmh,]最高速度为[200 kmh]。加速度传感器采用压电式加速度传感器SNy563,传感器安装位置如图3所示。
根据试验轮对及轴承的具体参数,计算各故障信息在速度[v0]时的故障频率如下:
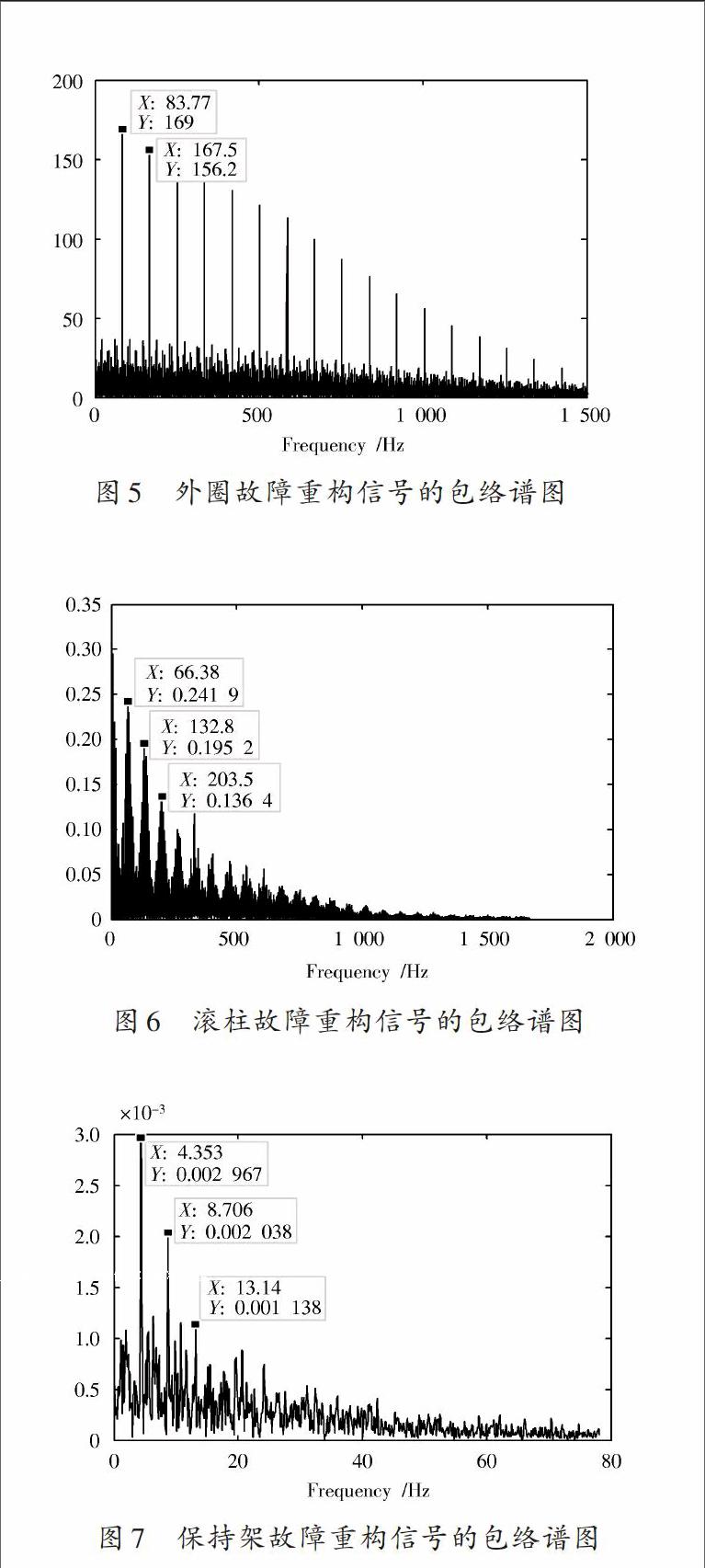
从图5中可以明显地看到一个83.77 Hz及其倍频的冲击信号。当轮对运行速度为[100 km/h]时,计算得到外圈故障频率[foc=83.30 Hz,]在忽略微小的转速误差的情况下,试验结果与理论计算高度吻合。
采用同样的方法,对滚柱故障信号和保持架故障信号进行处理,得到重构信号的包络谱图,如图6,图7所示。
图6中也包含一明显的冲击信号,其频率约为66.38 Hz,计算得到滚柱故障频率为[fb=33.93 Hz,]实测的故障频率约为理论故障频率的2倍,并远离其他故障频率,据此也可断定此故障发生在滚柱上。从图7中可以得出故障频率为4.35 Hz,与保持架故障频率[fc=4.39 Hz]相吻合。
6 结 论
本文综合运用EEMD分解、峭度计算和谱峭度分析,设计了一套列车轴承故障的诊断方法,并对各种故障轴承进行了振动试验。利用本文设计的诊断方法对试验数据进行了相应的分析,得到了振动信号的包络解调频谱图,由图中可以明显地看到冲击成分,这一冲击频率与理论计算的故障频率高度吻合,证明了本文设计的诊断方法的可行性。
参考文献
[1] 钟秉林,黄仁.机械故障诊断学[M].北京:机械工业出版社,2007.
[2] HARTING D R. Demodulated resonance analysis system : US, 3842663 [P]. 1974?03?12.
[3] MATHEW J, SZEZEPANIK A, KUHNALL B T, et al. Incipient damage detection in low speed bearings using demodulation resonance analysis technique [C]// Proceeding of 1987 ACT International Tribology Conference. Melbourne: ACT, 1987: 366?369.
[4] 康熊,黎国清,王卫东,等.基于共振解调技术的高速铁路焊接接头状态评判办法[J].中国铁道科学,2011,32(5):90?95.
[5] 王宏超,陈进,董广明,等.基于快速kurtogram算法的共振解调方法在滚动轴承故障特征提取中的应用[J].振动与冲击,2013,32(1):35?37.
[6] HUANG N E, SHEN Z, LONG S R, et al. The empirical mode decomposition and the Hilbert spectrum for non?linear and non?stationary time series analysis [J]. Proc. R. Soc. Lond. A, 1998, 454: 903?995.
[7] WU Zhaohua, HUANG N E. Ensemble empirical mode decomposition: a noise?assisted data analysis method [R]. Calverton: Center for Ocean?Land?Atmosphere Studies, 2005.
