基于FEKO的雷达目标电磁散射特性研究

李亭等

摘 要：为了验证电磁计算软件FEKO仿真计算雷达目标的电磁散射特性的可靠性，分别采用理论计算与仿真结果对比，紧缩场测量与仿真结果对比，FEKO仿真结果与HFSS仿真结果对比3种方式进行验证。发现理论计算、紧缩场测量以及HFSS仿真得到的单站RCS数据和FEKO仿真结果相吻合，由此验证了FEKO仿真结果的可靠性，可用于非合作目标电磁散射特性的仿真计算。

关键词： FEKO； 紧缩场测量； RCS； HFSS

中图分类号： TN955?34 文献标识码： A 文章编号： 1004?373X（2015）21?0039?03

Research on FEKO?based electromagnetic scattering characteristics of radar target

LI Ting， HAN Hongbin， LIU Yu

（Unit 91336 of PLA， Qinhuangdao 066326， China）

Abstract： To verify the reliability of electromagnetic scattering characteristics of radar target calculated by FEKO， three modes of comparing theoretical calculation with simulation results， comparing compact field measurement with simulation results， and comparing FEKO simulation results with HFSS simulation results are adopted for the verification. It′s found that the RCS data obtained from theoretical calculation， compact field measurement and HFSS simulation is be identical to FEKO simulation results. The reliability of FEKO simulation results is proved， and this method can be used to calculate and simulate the electromagnetic scattering characteristics of non?cooperative target.

Keywords： FEKO； compact field measurement； RCS； HFSS

0 引 言

雷达通常根据目标电磁散射特性确定其位置和类型，因此对目标电磁散射特性的研究在现代雷达对抗中具有重要意义[1?2]。目标电磁散射特性中最重要的是幅度特性，用雷达散射截面（RCS）来描述。在外场测量目标散射特性时常常会受到气候、温度、噪声等环境因素的影响而使得测量结果存在误差，因此常常需要与仿真计算结果进行比对来确定测量数据的有效性。

FEKO是一个以矩量法为基础的电磁计算软件，并且集成了物理光学法（PO）、几何绕射理论（GTD）、一致性绕射理论（UTD）、多层快速多极子法（MLFMA）等多种算法[3]。RCS的仿真计算很多都是采用FEKO软件完成，因此对FEKO计算结果可靠性的验证必不可少。本文分别采用理论计算与仿真结果对比，紧缩场测量与仿真结果对比，FEKO与HFSS仿真结果对比3种方式验证FEKO计算的可靠性。

1 FEKO的仿真计算方法

利用电磁计算软件FEKO仿真计算雷达目标电磁散射特性时，首先建立其几何模型，并赋予其材料特性和激励条件；然后对模型进行网格化剖分，建立其几何结构的数据文件，利用相应的电磁计算方法对其进行近似求解；最后通过对计算结果的处理得到想要的数据。具体过程如图1所示。

2 目标电磁散射特性分析

雷达根据目标对雷达波的散射能量来判断目标存在并确定目标位置，对目标电磁散射特性的研究在现代雷达对抗中具有重要意义。目标电磁散射特性中最重要的是幅度特性，通常用雷达散射截面（RCS）描述。它是目标的假想面积，用一个各向均匀的等效反射器的投影面积表示，该等效反射器与被定义的目标物体，在接收方向单位立体角内具有相同的回波功率。雷达散射截面一般用符号[σ]表示，其数学定义为[4?6]：

式中：[r0]是平板面元局部坐标系原点在全局坐标系中的位置矢量；[am]是平板面元第[m]个边缘的长度和方向矢量；[rm]是第[m]个边缘中点的位置矢量；[W=i-s，][i，][s]分别为入射和散射方向的单位矢量；[T]是[W]在平板面元上的投影长度；[p=n×Wn×W]是平板面元上垂直于[W]的单位矢量；[M]是平板边缘的数目，取3时即为三角形面元。

尖劈的RCS平方根公式由PTD推得[1]：

3 基于FEKO的仿真分析

3.1 金属平板的FEKO仿真与理论计算对比

设一个理想导电的矩形金属平板在[xOy]平面上，长宽分别为[a]和[b，][a=b=]30 cm，如图2所示。

采用FEKO软件仿真计算金属平板在9.41 GHz频点的入射波照射下，不同方位（[θ]=90°，[φ]=0°～90°，间隔为0.5°）的单站RCS值。对有限尺寸的平板的理论计算有物理光学法（PO）、几何绕射理论（GTD）和一致性绕射理论（UTD）三种计算方法。将仿真得到的垂直极化和水平极化两个分量与理论计算结果进行对比，如图3所示。

由图3可以看出，在[0≤φ<25°]范围内，仿真结果与理论计算值相同，而超过这个范围后，理论PO算法与FEKO仿真计算值偏差较大，而GTD和UTD结果与理论计算值较为相近，这是由于PO未能考虑金属平板前后面之间的多次绕射。

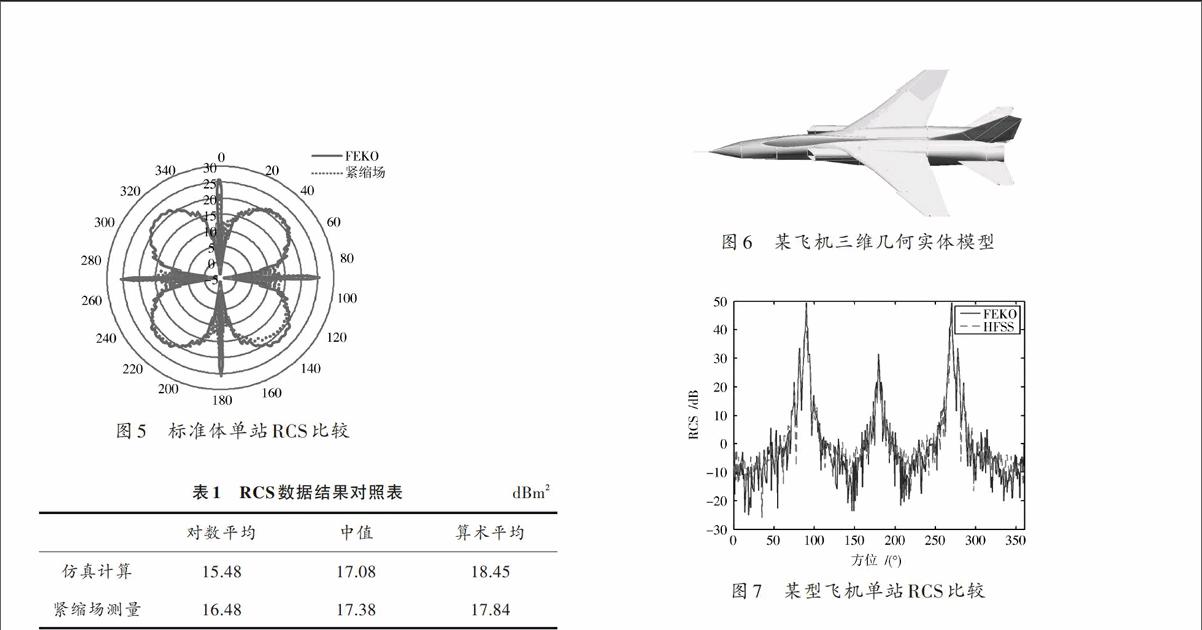
3.2 标准体的FEKO仿真与实测数据对比

选择如图4所示的5 m2三维几何实体目标作为标准体，该标准体边长为448 mm，倒角边长为53.5 mm，金属板厚度为1 mm。

由仿真计算结果和实测结果均可看出：在平面波正对标准体垂直入射时（0°，90°，180°，270°四个方位），标准体的RCS值最大，此时标准体的散射截面最大。当入射方向在45°，135°，225°和315°时，标准体RCS均出现一个极值，此时标准体的散射截面相当于其中两个角反射体相对于入射方向的横截面积。

FEKO仿真和紧缩场测量的RCS最大值和平均值的比较如表1所示。从表1中可以看出，FEKO仿真和暗室测量对数平均值相差1 dB，中值相差0.3 dB，算术平均值相差0.61 dB。由此可以看出仿真结果与紧缩场测量十分接近。

4 结 语

通过以上对比分析可以得出，FEKO能够方便快捷地解决雷达目标电磁散射特性计算问题，计算结果与理论计算、紧缩场测量以及HFSS仿真结果相吻合，计算精准度较高，可用于非合作目标电磁散射特性的仿真计算。为以后在仿真实验中采用FEKO计算复杂雷达目标电磁散射特性结果的正确性奠定了理论支撑。

参考文献

[1] 计科峰，王世唏.空间目标宽带雷达特征信号仿真建模[J].现代雷达，2007，29（3）：32?36.

[2] 黄培康，殷红成，许小剑.雷达目标特性[M].北京：电子工业出版社，2005.

[3] 陈德喜，颜俐，王海婴.FEKO软件的RCS仿真应用[J].舰船电子工程，2008，28（9）：125?128.

[4] LI H J， YANG S H. Using range profiles as feature vectors to identify aerospace objects [J]. IEEE Transactions on Antennas and Propagation， 1993， 141（3）： 261?266.

[5] 陈军.近远场天线测量系统与定标体RCS的研究[D].西安：西安电子科技大学，2012.

[6] 范宇.复合结构飞行器翼面RCS的数值计算[D].成都：电子科技大学，2004.

[7] 严靖峰，徐鹏根.RCS预估中图形电磁学方法的改进[J].电波科学学报，1998，13（3）：313?317.

[8] 杨端义.复杂目标雷达散射截面的分析方法[D].南京：南京理工大学，2009.

[9] 刘良，李淑华.高低频混合方法估算角反射器阵RCS[J].现代电子技术，2014，37（15）：12?14.