基于神经网络的桥梁施工控制研究
2015-11-08谢颂诗齐钦
谢颂诗,齐钦
(1.天津市市政工程设计研究院,天津市300051;2.天津城建设计院有限公司,天津市300130)
基于神经网络的桥梁施工控制研究
谢颂诗1,齐钦2
(1.天津市市政工程设计研究院,天津市300051;2.天津城建设计院有限公司,天津市300130)
将神经网络方法结合Matlab用于处理大跨度预应力混凝土连续梁桥施工控制中的箱粱线形控制的误差预测和调整。由于受诸多因素影响,标高的实测值与理论计算值有一定的差异,只有通过前期预测和后期调整相结合,才能保证成桥实际状态同设计要求一致。神经网络可利用实测样本的自学习达到到此目的。应用实例表明神经网络法的预测精度高,这对同类桥梁的施工控制具有一定指导意义。
神经网络; Matlab; 预应力连续梁桥; 施工控制; 误差预测和调整
0 引言
在大跨度桥梁的实际施工中,虽然可采用各种施工计算方法算出各施工阶段的预拱度值、挠度等控制参数,但是按这些理论值进行施工时,结构的实际变形却未必能达到预期的结果。造成误差的原因是多方面的,其中包括:设计参数的误差、施工误差、测量误差等。就施工截面的标高而言,实际测量值与理论计算值的偏差是以上误差综合影响的结果。施工控制的任务是使桥梁结构的实际状态尽可能地与理论状态相一致,其手段是通过前期预测和后期调整来实现。
BP网络是目前应用最为广泛的一类神经网络,因采用在l986年问世的反向传播法(Back Propagation)算法而得名。神经网络的预测能力是通过自学习得到的。由于样本的期望输出为测量的标高,实际值难免包含某些随机因素和误差,甚至个别数据存在明显的不符合普遍规律的情形,网络必须有对这类样本的鉴别能力。BP神经网络具备此类功能网络的输出并非要求严格地等于各样本的期望输出,而是通过网络学习,寻求对全部样本数据均有较好响应的非线性映射关系。因此,可以作为处理有随机干扰问题的预测工具。
1 BP神经网络
1.1基本原理
BP网络是人工神经网络的一种,它可以通过对若干样本的自学习,建立网络输入变量与输出变量之间的全局非线性映射关系。本文将以三层BP神经网络为例,介绍网络的学习规则和误差反向传播法的基本原理。
三层BP神经网络如图1所示,其构成包括输入层、隐含层和输出层,同层单元之间互不相连。BP算法的学习过程由正向传播和反向传播组成。正向传播过程中,输入模式是从输入层经隐含层逐层处理,并传向输出层,每一层神经元的状态仅影响下一层神经元的状态。如果在输出层不能得到期望的输出,则转入反向传播,将误差信号沿原来的连接通路返回,通过修改各神经元的权值,使得误差信号为最小。实际上,误差达到人们所希望的要求时,网络学习过程就告结束。BP算法是适合于多层神经元网络的一种学习,它是建立在梯度下降法的基础上的。
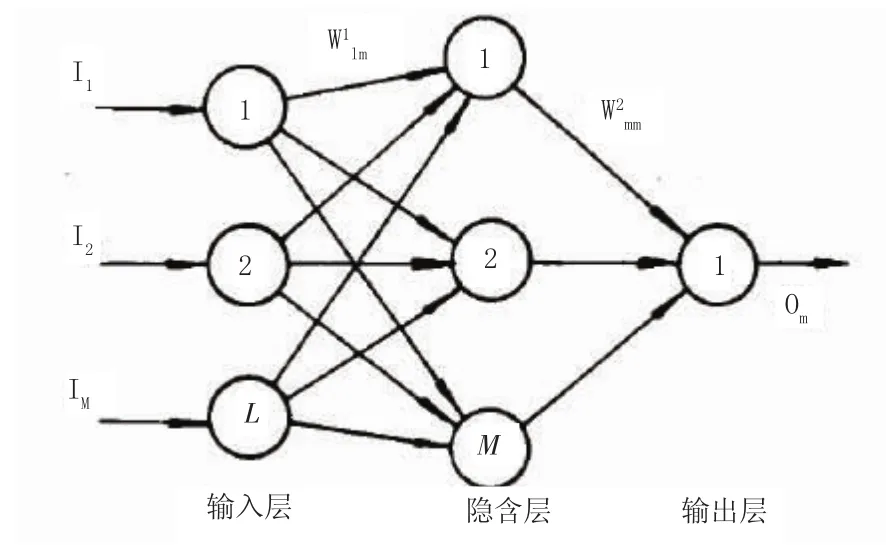
图1 三层BP神经网络结构图
对于本文中的三层网络,输入层和输出层有与网络输入变量Il(l=1,2,…,L)及输出变量On(n=1,2,…,N)相应的L和N个神经元,而隐含层取M(M=2L+1)个神经元。输入层可直接按规则输入到隐含层;而隐含层只接受输入层的输出信息,经过作用函数后,再把隐含节点的输出信息输出给输出层;输出层只接受隐含层的输出信息,经过作用函数后输出最终结果。节点作用函数通常选用S(Sigmoid)型函数,如:

设给定任意N个样本(xk,yk()k=1,2,…N),对于第k个样本,现在研究第(ll=2,3)层的第j个节点,第l-1层的节点i的输出为,节点j的输入为,则:

使用平方型误差函数:

其中,yk,为网络的实际输出,则总误差为:


下面对节点j分两种情况讨论:

(2)若节点j不为网络输出节点时,则:

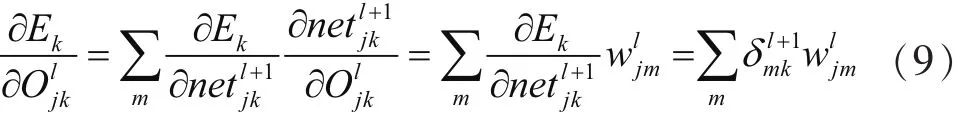
由(8)和(9)两式可得:
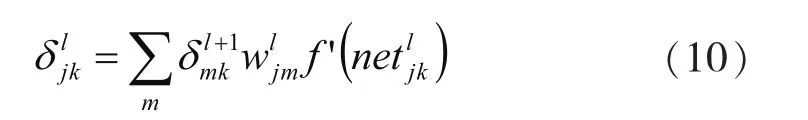
对于本文所讨论的问题,即l=2,此时(l-1)层也就是第三层只有一个单元,故上式可简化为:
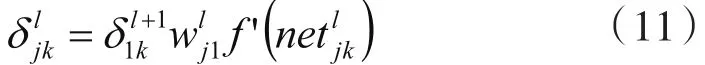
其中,1代表第三层只有1个节点。
1.2BP网络算法
BP网络的逼近能力和训练方法是其应用的关键,其算法实现的过程为:
(1)选定权系数初值。
(2)重复下述过程直到收敛。
对于k=1到N:
(3)修正权值。按误差反向传播方向,从输出单元开始返回到隐含层,按下式修正权值:

(4)调整后再返回到过程(2)训练,经过不断地调整和训练,直到误差满足要求为止。这样,网络才算是训练成熟,映射性态稳定,才可投人使用。
2 BP 网络的实现
2.1输入输出参数的确定
连续梁桥的每节段是按挂篮前移立模扎筋、浇筑混凝土与养护,以及张拉预应力筋等三个主要施工工序进行。实测表明前两道工序的标高一般与理论计算值的偏差并不大,仅为毫米级,通常在张拉预应力后则会出现较大的偏差,尤其是预应力筋较长时的偏差显著,施工控制中必须先对桥面标高的偏差进行合理的预测,以便及时调整。
BP网络输入层节点数(神经元个数),在本文中即为所考虑的在桥梁施工中引起标高偏差的影响因素的个数。这类影响因素很多,如果将所有因素均予以考虑,则势必会增加分析的难度,而且也没有必要。为了使分析简单化,经过分析,在模型中只考虑以下主要因素:张拉截面、讨论截面的箱梁高度I1、I2;它们到“T”构墩中心的距离L1、L2;理论计算的张拉后标高的变化值W,共计5个参数,样本的期望输出为预测的标高偏差△W,各变量汇总见表1所列。由此建立3层BP网络模型,输入层设计5个神经元,输出层设计1个神经元,隐含层中神经元的个数为2×5+1=11个。

表1 神经网络输入和输出参数表
2.2BP网络在Matlab中的实现
本文利用Matlab建立神经网络,使得建模方便,省去了重复建模的繁琐,让网络训练时上万次的迭代在很短的时间内完成。利用Matlab编程建模具体包括以下几步:
(1)确定网络训练集,包括输入向量和目标向量;
(2)对网络训练集进行正规化处理;
(3)对正规化处理后的向量进行主成分分析,去除次要数据;
(4)建立并训练网络;
(5)对网络输出和相应的目标进行线性回归,以判断网络的优劣;
(6)利用网络进行预测。
3 实例应用
北京环线某组合连续梁桥(桥跨布置见图2)。桥梁全长为249.5 m,计算跨度为(60+128+60)m,上部为拱梁组合体系,梁底下缘按二次抛物线变化,边支座中心线至梁端0.75m。该桥采用挂篮悬臂施工方式。本文涉及的梁体施工过程的标高预测和调整。

图2 北京环线连续梁桥桥跨布置图
混凝土连续梁桥的成桥线形在施工中是通过现浇各节段的立模标高来控制的,控制的过程为一个施工-量测-识别-修正-预告-施工的循环过程。每浇筑完一个节段,挂篮前移,先前施工完成的悬臂各节段均会产生一定的下挠变形,通过对各节段上标高的测量形成一组桥面实测标高与设计标高的偏差值,通过对引起误差的参数进行识别和修正,确定下一节段的立模标高,最终完成整个线形控制过程。
以下将讨论用神经网络预测程序对实际发生的桥面标高偏差预测的实施。以该桥160号墩为例,假设施工到达n节段,则以前n-1阶段的实测数据为训练集形成输入矢量P和输出矢量t,建立网络并进行训练,并查看线性回归的结果,然后预测第n节段的标高偏差,网络训练过程和线性回归的结果,见图3和图4所示。在网络训练过程中,网络总误差取0.05,最大循环次数取100 000次。实践证明在达到最大循环次数之前都能满足网络总误差的要求,并且体现网络训练优劣的参数R都在0.965以上。
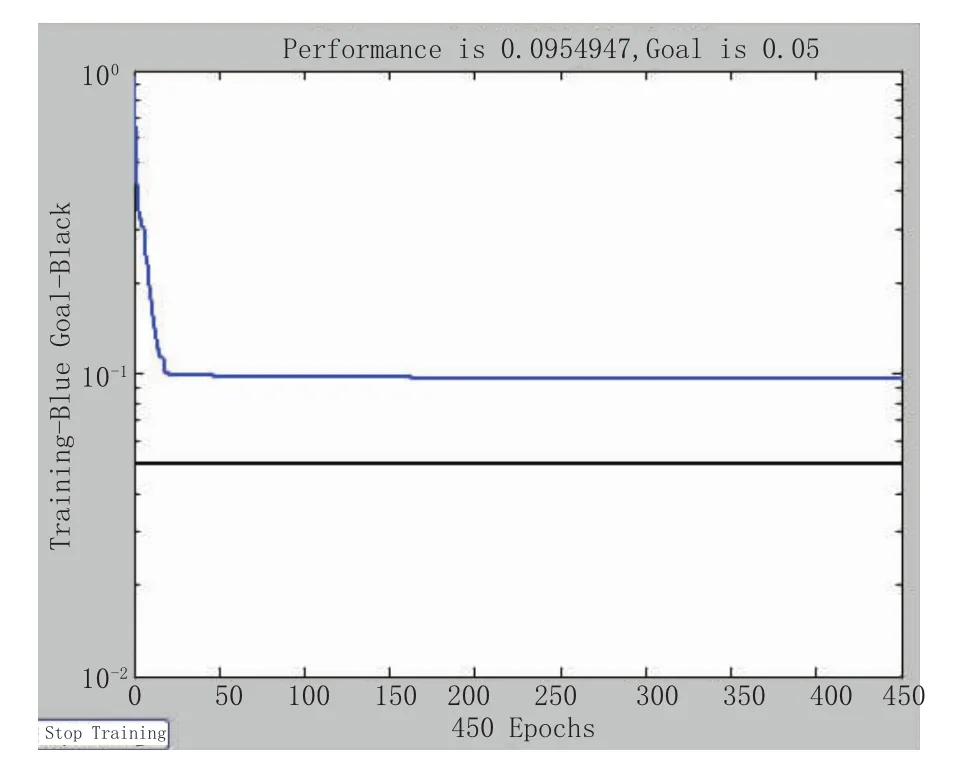
图3 BP神经网络训练过程图示
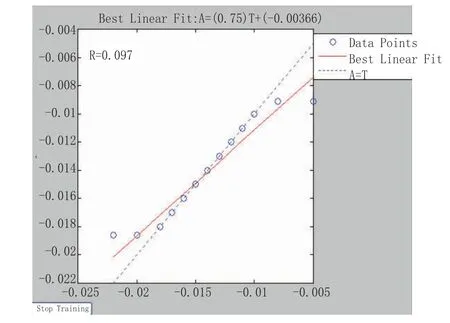
图4 线性回归的结果图示
现将第11至15节段网络为例来说明预测成果。网络训练后用于预测的输入参数值及网络输出,见表2所列。标高偏差理论计算值、期望输出和BP网络输出的结果的对比,见图5所示。在图5中,期望输出即实测值,BP网络输出即预测值。

表2 神经网络输入参数和输出结果一览表
U445
A
1009-7716(2015)06-0202-03
2015-02-04
谢颂诗(1983-),男,山东曹县人,硕士研究生,工程师,从事桥梁工程设计研究工作。
