椭圆曲线底层域快速算法的优化

赖忠喜，张占军

台州职业技术学院机电工程学院，浙江台州318000

椭圆曲线底层域快速算法的优化

赖忠喜，张占军

台州职业技术学院机电工程学院，浙江台州318000

为了提高椭圆曲线底层域运算的效率，基于将乘法转换为平方运算的思想，提出在素数域FP上用雅克比坐标直接计算2kP和3kP的改进算法，其运算量分别为（3k-1）M+（5k+3）S和（6k-1）M+（9k+3）S，与DIMITROY和周梦等人所提的算法相比，算法效率分别提升了6.25%和5%。另外，利用相同的原理，给出了素数域FP上用在仿射坐标系直接计算3kP的改进算法，其运算量为I+（6k+1）M+（9k+1）S，与周梦和殷新春等人所提的算法相比，效率分别提升了3.4%和24%。

椭圆曲线密码体制；标量乘法；底层域运算；仿射坐标；雅克比坐标

1　引言

1985年，Koblitz和Miller分别提出了一种新的公钥算法—椭圆曲线密码体制（Elliptic Curve Cryptography，ECC），由于其安全性高和实现性能优等独特的优势逐步成为国内外学者研究的重点［1-2］。实现椭圆曲线密码体制最耗时的运算是椭圆曲线标量乘法，即kP的计算，其运算速度从整体上决定了ECC的实现效率［3］。研究标量乘法通常可从两个方面来考虑，一方面是研究标量k的有效表示，尽量减少上层的运算，如k的三元表示、非相邻表示（Non-adjacent form，NAF）、w-NAF、双基数系统［4-5］（Double-base number system，DBNS）及多基数系统［6］（Multi-Base Number System，MBNS）等表示形式。另一方面是对底层域快速算法进行研究，以减少底层域的运算量。目前文献中，对提高底层域运算效率的方法可以归纳为：

（1）通过坐标变换，避免求逆。Mahdavi［7］等人对点P进行坐标变换（标准投影坐标、Jacobian坐标、改进的Jacobian坐标、Chudnovsky坐标等），这种方法通过改变点的坐标形式，继而不要求逆，提高了运算效率。

（2）将求逆运算转换为乘法运算。Sakai［8］等人利用求逆转化为乘法的思想推导出了FP上计算2kP的算法。Dimitroy［9］等人提出了雅克比坐标系下直接计算2kP和3kP的算法。Ciet［10］等人利用分母的最小公倍数思想，对2P+Q、3P、3P+Q、4P、4P+Q等底层域运算进行优化。Mishra［6］等人利用除法多项式提出了计算5P的快速算法。之后殷新春［3］等人推导出仿射坐标系下直接计算3kP的快速算法，徐凯平［11］等人改进了计算5P的算法并给出了在仿射坐标系下直接计算5kP的快速算法，Duc-Phong［12］改进了计算4P算法，进一步提高了效率。

（3）将乘法运算转换为平方运算。Joye［13］利用转换乘法为平方的思想，改进了雅克比坐标系下的P+Q和2P运算，Patrick［14］改进了雅克比坐标系下直接计算3P、5P、7P等运算，之后周梦［15］等人改进了雅克比坐标系下计算3P和3kP的算法，并给出了FP上计算2kP和3kP的改进算法。所有的这些算法减少了底层域的运算量，加快了椭圆曲线标量乘的运算速度。

本文利用将乘法转化为平方运算的思想，提出在素数域FP上用雅克比坐标直接计算2kP和3kP的改进算法，与DIMITROY和周梦等人所提的算法相比，新算法效率分别提升了6.25%和5%。另外，本文给出了素数域FP上用仿射坐标系直接计算3kP的改进算法。与周梦和殷新春等人所提的算法相比，新算法效率分别提升了3.4%和24%。

2　背景知识

定义在素数域FP上的椭圆曲线E:y2=x3+ax2+b；（a，b∈FP且，Δ=4a3+27b3≠0）的点满足该曲线方程的所有解称为该椭圆曲线上的有理点，椭圆曲线E上的所有有理点再加上一个被称为无穷远的点O构成了一个加法交换群，椭圆曲线E的群运算是按照椭圆曲线群运算法则完成的，其中所涉及的运算有加、减、乘、求逆和平方五种基本运算，分别用I、S、M表示域FP上求逆，平方和乘法运算。五种基本运算中，加法和减法相对于其他运算来说，所用时间可忽略不计［11］。这里假设I= 10M，S=0.6M［15］。

2.1仿射坐标系下的运算法则

令P=（x1，y1）∈E（FP），Q=（x2，y2）∈E（FP），P≠±Q，则P+Q=（x3，y3）∈E（FP）可由式（1）计算：

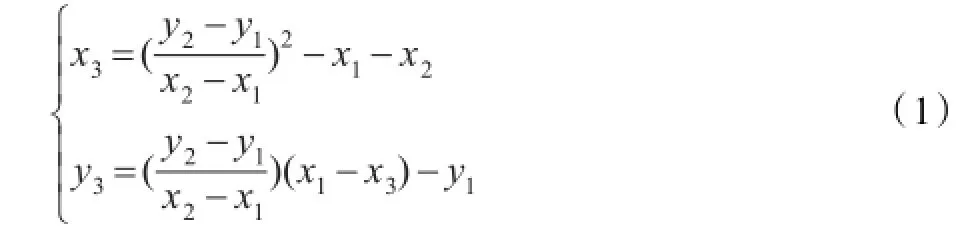
令P=（x1，y1）∈E（FP），P≠-P，则2P=（x3，y3）∈E（FP）可由式（2）计算：

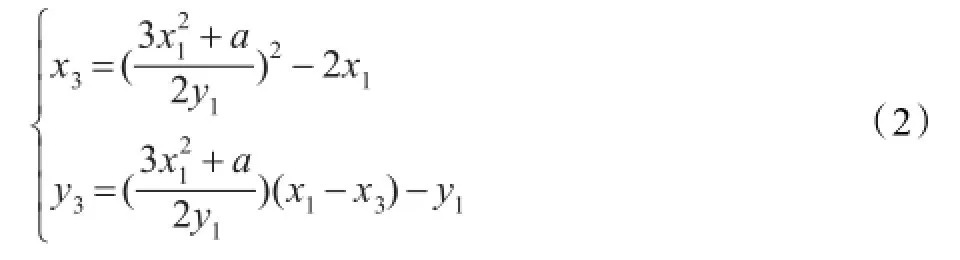
由式（1）和式（2）可知，素数域FP上完成点加运算和倍点运算的运算量分别为I+2M+S和I+2M+2S。

2.2雅克比坐标系下的运算法则

令c=2，d=3，则雅克比投影坐标P=（X，Y，Z）与仿射坐标P′=（x，y）=（X/Z2，Y/Z3）相对应。在雅克比坐标系下椭圆曲线方程为E:Y2=X3+axZ4+bZ6。

令P=（X1，Y1，Z1）∈E，Q=（X2，Y2，Z2）∈E，P≠±Q，则P+Q=（X3，Y3，Z3）可由式（3）计算

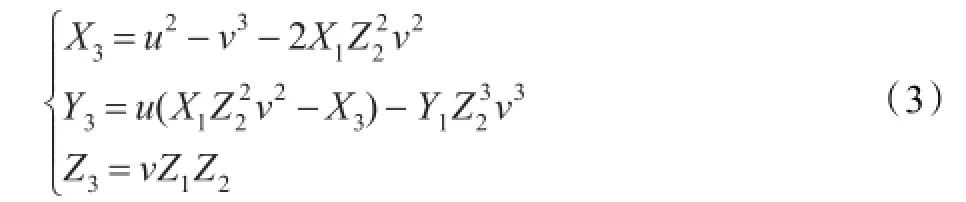
令P=（X1，Y1，Z1）∈E，P≠-P，则2P=（X3，Y3，Z3）可由式（4）计算。

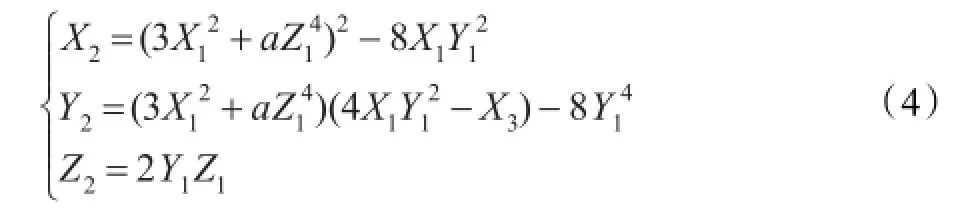
通过分析存储中间结果可知，雅克比坐标下下计算2P所需的运算量为4M+6S。

3　雅克比坐标系下2kP的改进

如果将标量表示成2k的形式，那么直接计算2kP会大大提高计算效率。文献［9］给出了雅克比坐标系下直接计算2kP的详细计算过程，本章利用将求逆转化为乘法的思想和等式2ab=（a+b）2-a2-b2在文献［9］的基础上改进了雅克比坐标系下直接计算2kP的算法，具体步骤如算法1所示，具体运算量见表1。

表1　算法1的运算量

算法1雅克比坐标系下计算2kP的改进算法

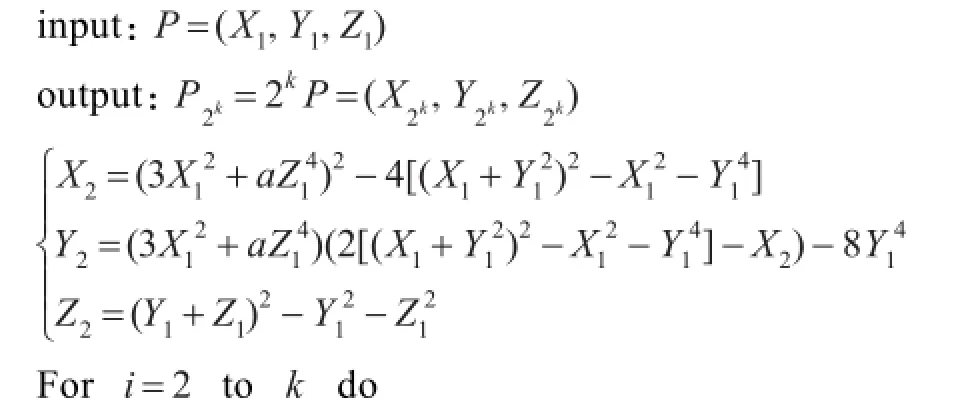
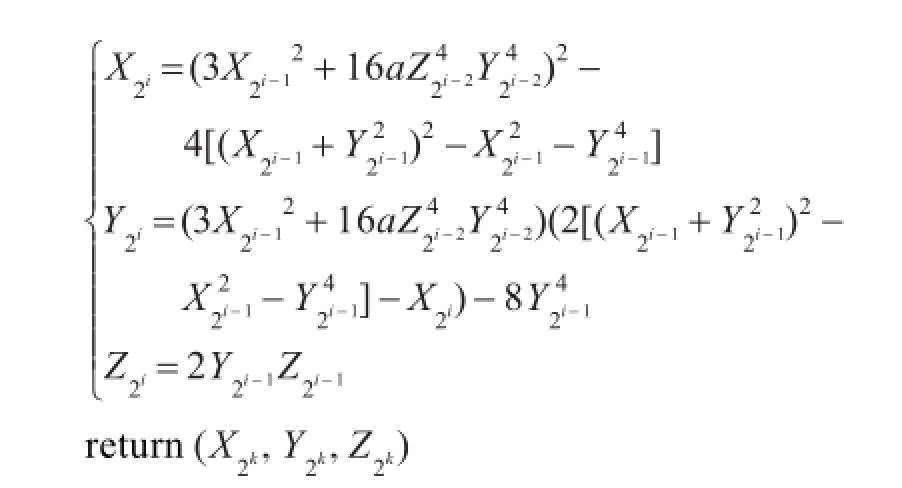
4　雅克比坐标系下3kP的改进

如果将标量表示成3k的形式，那么直接计算3kP会大大提高计算效率。文献［15］利用转换乘法为平方运算的代数方法，给出了雅克比坐标下计算3kP的算法，本章延续将乘法转化为平方的思想，利用等式2ab=（a+b）2-a2-b2在文献［15］的基础上进一步改进雅克比坐标系下直接计算3kP的算法，具体步骤如算法2所示，具体运算量见表2。

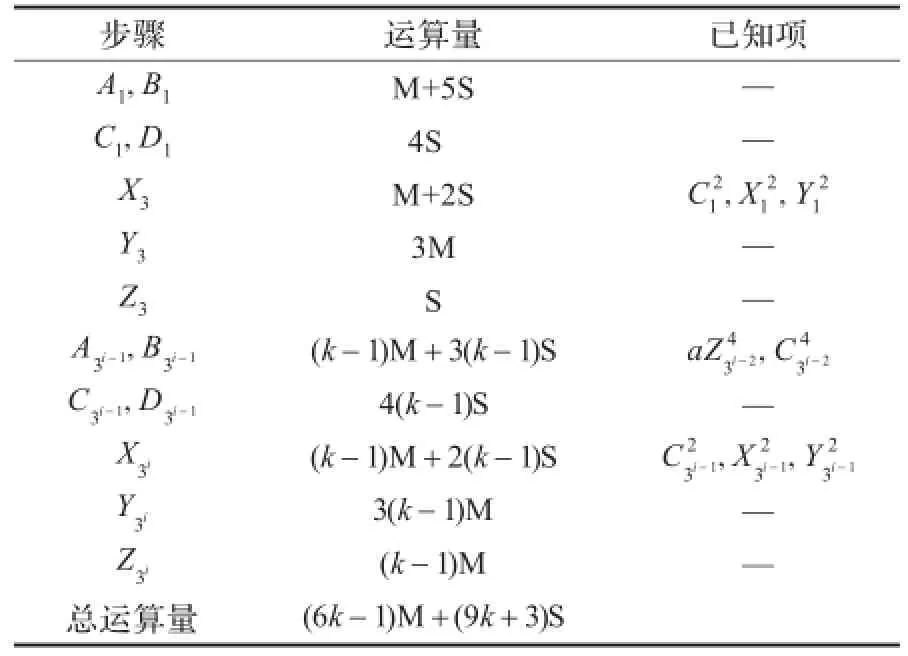
表2　算法2的运算量

算法2雅克比坐标计算3kP的改进算法

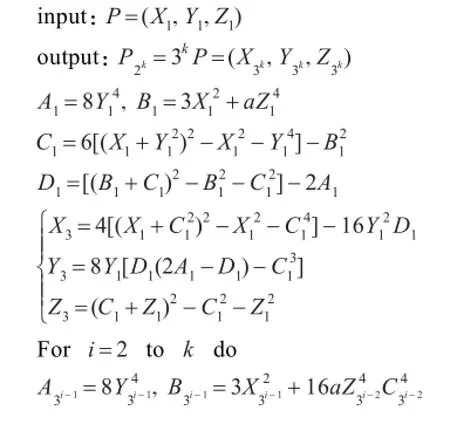
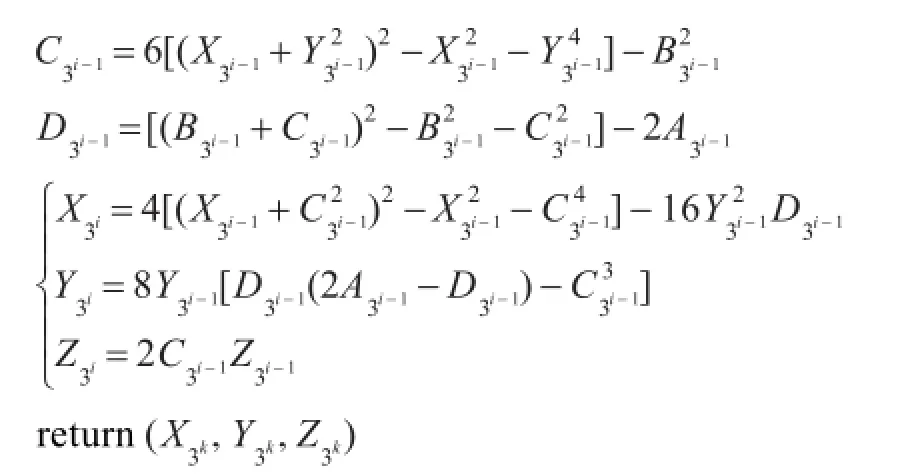
在算法2中，当分析计算 B3i-1运算量时，由于已在上个循环计算出来，所以计算 B3i-1只需（k-1）M+（k-1）S运算，经过分析可知算法2总的运算量为（6k-1）M+（9k+3）S。比文献［15］中计算3kP时的运算量6kM+10kS相比，减少了（0.6k-0.8）M，效率提升了5%。比文献［9］中计算3kP时的运算量（11k-1）M+（4k+2）S相比，减少了（2k-0.6）M，效率提升了14.9%。

表3列出了素数域上在雅克比坐标系下不同运算的开销。

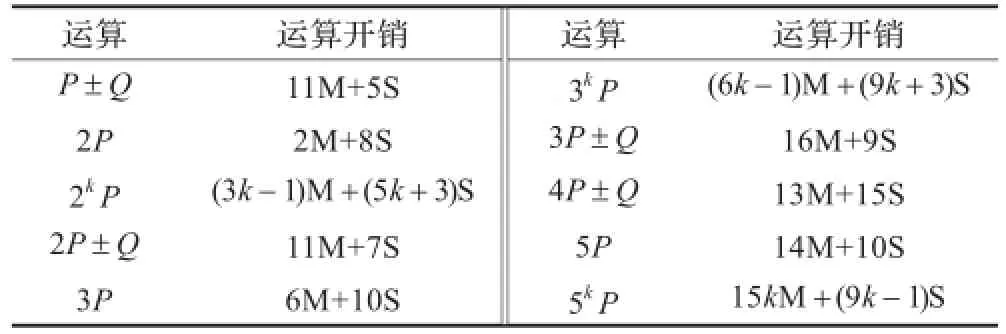
表3　素数域中不同运算的开销（雅克比坐标系）

5　仿射坐标系下计算3kP的改进算法

令P=（x1，y1）∈E（FP），3kP=（x3k，y3k）∈E（FP）。本章延续上章相同的思想，在文献［15］的基础上给出了仿射坐标系下直接计算3kP的改进算法，具体步骤如算法3所示，具体运算量见表4。

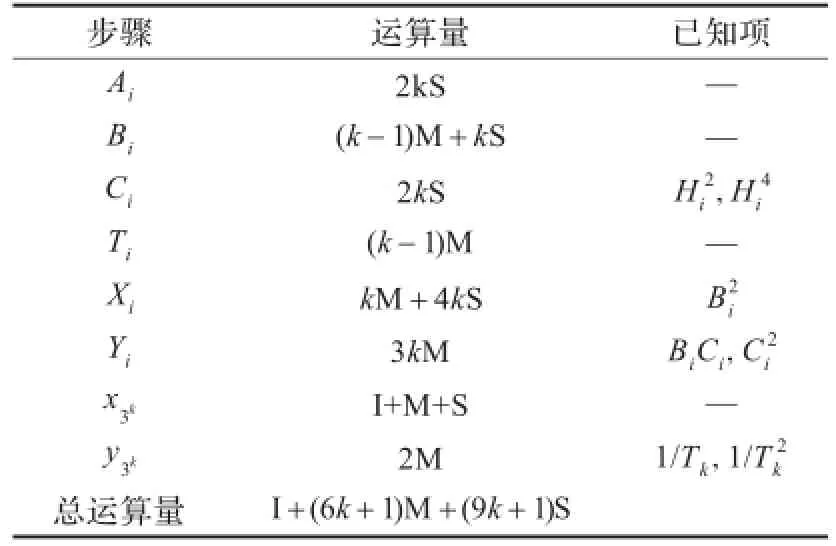
表4　算法3的运算量

算法3仿射坐标系下计算3kP的改进算法

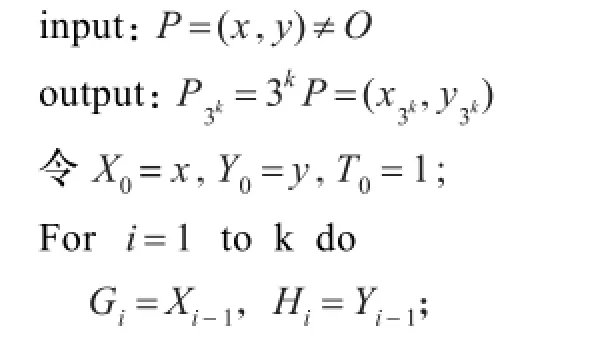
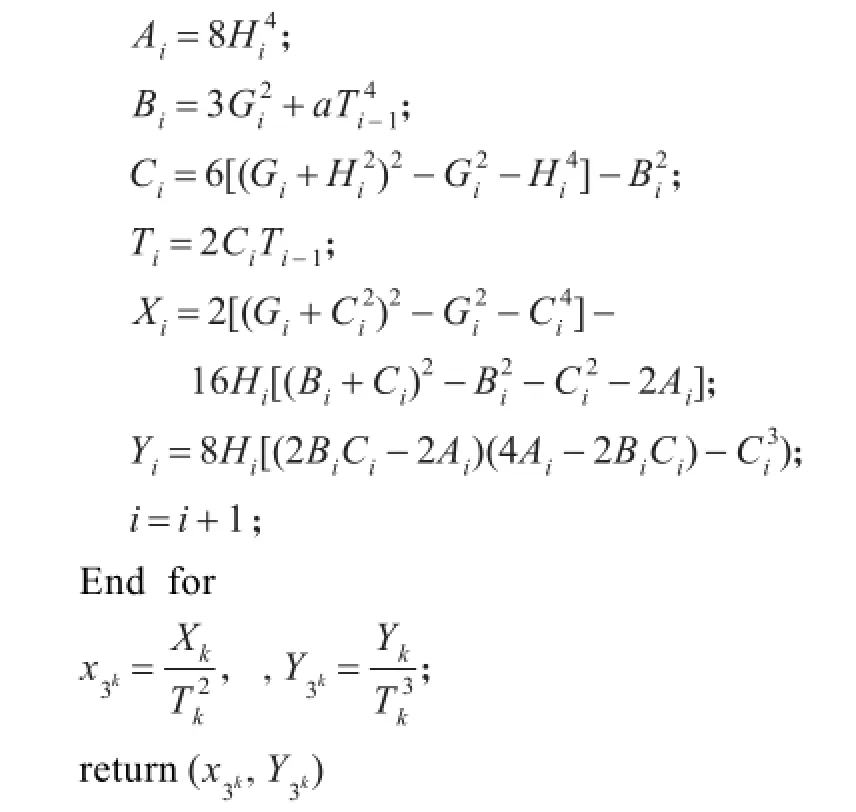
6　结束语

本文利用将乘法化为平方的思想，研究了域K（FP）特征大于3的椭圆曲线，给出了雅克比标系下直接计算2kP和3kP的改进算法，与文献［9］和文献［15］中计算2kP和3kP的运算量相比，新算法分别节省了（0.4k+0.6）M和（0.6k-0.8）M的运算量，运算效率分别提升了6.25%和5%，另外，利用相同的思想，本文在仿射坐标系下给出计算3kP的改进算法，与文献［15］和文献［3］中计算3kP运算量相比，新算法分别减少了（0.4k-0.2）M和（3.6k-1）M运算，算法的运算效率分别提升了3.4%和24%。下一步工作应考虑将乘法转换为平方的思想应用在计算5P、7P、5kP和7kP等底层域算法中。

［1］赖忠喜，张占军，陶东娅.椭圆曲线中直接计算7P的方法及其应［J］.计算机应用，2013，33（7）：1870-1874.

［2］Hankerso D，Menezes A，Vanstone S.Guide to elliptic curve cryptography［M］.New York：Springer-verlag，2004：76-81.

［3］殷新春，侯洪祥，谢立.基于双基数的快速标量乘算法［J］.计算机科学，2008，35（6）：186-195.

［4］Dimitrov V S，Imbert L，Mishra P K.Fast elliptic curve pointmultiplicationusingdouble-basechains［EB/OL］.［2007-04-10］.http//eprint.iacr.org/2005/069.

［5］Dimitrov V S，Jullien G A.A new number representation with applications［J］.IEEE Circuits and Systems Magazine，2003（2）：6-23.

［6］Mishra P K，Dimitrov V.Efficient quintuple formulas for elliptic curves and efficient scalar multiplication using multibase number representation［C］//Proceedings of the 10th Information Security Conference.Berlin：Springer-Verlag，2007：390-406.

［7］Mahdavi R，Saiadian A.Efficient scalar multiplications for elliptic curve cryptosystems using mixed coordinates strategy and direct computations［M］//Cryptology and Network Security.Berlin Heidelberg：Springer，2010：184-198.

［8］Sakuraik S.Efficient scalar multiplications on elliptic curves with direct computations of several doublings［J］.IEEE Transactions on Fundamentals，2001，E84-A（1）：120-129.

［9］Dimitroy V，Imvert L，Mishra P K.Efficient and secure elliptic curve point multiplication using double base chain［C］//Proceedings of the 11th International Conference on the Theory and Application of Cryptology and Information Security. LNCS 3788.Chennai：Springer-Verlag，2005：59-78.

［10］Ciet M，Joye M，Lauter K，et al.Trading inversions for multiplications in elliptic curve cryptography［J］.Designs Codes and Cryptography，2006，39（2）：189-206.

［11］徐凯平，郑洪源，刘锦峰，等.椭圆曲线密码体制中快速标量乘方法研究［J］.计算机工程与应用，2011，47（15）：112-115.

［12］Le Duc-Phong.Fast quadrupling of a point in elliptic curve cryptography［EB/OL］.［2011-06-10］.http//eprint.iacr. org/2011/039.

［13］Joye M.Fast point multiplication on elliptic curves without pre-computation［C］//Procof the2ndInternational Workshop on Arithmetic of Finite Fields，Siena.Berlin：Springer，2008：36-46.

［14］Longa P.High-speed elliptic curve and pairing-based Cryptography［D］.Ottawa：University of Ottawa，2011.

［15］周梦，周海波.椭圆曲线快速点乘算法优化［J］.计算机应用研究，2012，29（8）：3056-3058.

Optimizing fast field operation in elliptic curves.

LAI Zhongxi，ZHANG Zhanjun

College of Mechanical and Electrical Engineering，Taizhou Vocational Technical，Taizhou，Zhejiang 318000，China

To raise the efficiency of field operation on elliptic curve，based on the idea of trading multiplications for squares，two modified algorithms are proposed to compute 4P and 5P directly over prime fieldFPin terms of affine coordinates，their computational complexity are（3k-1）M+（5k+3）Sand（6k-1）M+（9k+3）Srespectively，which are improved to 6.25%and 5%respectively than those of Dimitroy’s and Zhou meng’s method.Moreover，using the same idea，an improved method is given to compute3kPdirectly in terms of affine coordinates，its computational complexity is I+（6k+1）M+（9k+1）S，and the efficiency of the new method is improved to 3.4%and 24%respectively than those of Zhong meng’s and Yin xin-chun’s method.

elliptic curve cryptosystem；scalar multiplication；field operation；affine coordinate；jacobian coordinate

A

TP309.7

10.3778/j.issn.1002-8331.1311-0238

浙江省教育厅科研项目资助（No.Y201533946）。

赖忠喜（1984—），男，讲师，CFF会员，主要研究方向：信息安全、智能控制；张占军（1979—），男，讲师，主要研究方向：信息安全、智能控制。E-mail：laizhongxi@163.com

2013-11-17

2014-01-13

1002-8331（2015）22-0115-04

CNKI网络优先出版：2014-04-01，http://www.cnki.net/kcms/doi/10.3778/j.issn.1002-8331.1311-0238.html