深基坑排桩支护结构优化设计
2015-11-04丁敏穆健
丁敏 穆健
(重庆市巴南区公路工程质量监督站 重庆 401320)
深基坑排桩支护结构优化设计
丁敏穆健
(重庆市巴南区公路工程质量监督站重庆401320)
对深基坑工程排桩支护结构优化设计的进行了数学解释,描述了设计变量的选择、约束条件的确定、目标函数的确立三方面的内容。对排桩的相关设计变量进行了敏感性分析,挑选出对优化目标影响较大的设计变量,概括出排桩支护结构的主要约束条件,确定以综合造价为优化目标的最终优化目标函数,从而建立了深基坑排桩支护结构优化设计数学模型。
排桩;约束条件;敏感性分析
前言
深基坑支护工程的优化设计依据其设计阶段不同,可分为两大类,即方案优化设计和结构优化设计。方案优化设计是根据深基坑工程诸多方面需求,对各个可行的支护方案进行比较,从中优选出最佳支护方案。针对深基坑优化的问题,本文重点研究了深基坑排桩支护结构形式的设计变量选择、约束条件确定、目标函数确立以及优化设计模型建立的等方面内容。
1 设计变量的确定
深基坑排桩支护结构的设计变量分为支护桩结构和支撑结构。排桩的关键设计变量有:桩径、桩中心距、桩嵌固深度、混凝土强度等级和支撑位置等[2]。
为了合理确定优化设计变量取值范围,通过实例对设计变量参数做了敏感性分析。基坑实例:基坑深度16m,土层分五层。其力学性质指标是分别是:c1=12kPa,φ1=11°,γ1=19kN/m3,厚度H1=2m;c2=20kPa,φ2=17°,γ2=19kN/m3,厚度H2=2.5m;c3=10kPa,φ3= 12°,γ3=19kN/m3,厚度H3=9m;c4=25kPa,φ4=27°,γ4=21kN/m3,厚度H4=1.5m;c5=36kPa,φ5=32°,γ5=20.5kN/m3,厚度H5=10m;坡顶荷载q=20kN/m。
1.1桩径及桩中心距
如图1所示,桩身最大位移值随着桩径dp的增大而逐渐减小。当桩径小于1.2m时,最大位移值变化较为明显;当桩径大于1.2m时,最大位移值变化趋势趋于平缓[4]。由此,可以得出这样的结论,合理地提高桩径对排桩支护结构的安全稳定性有着显著的改善。
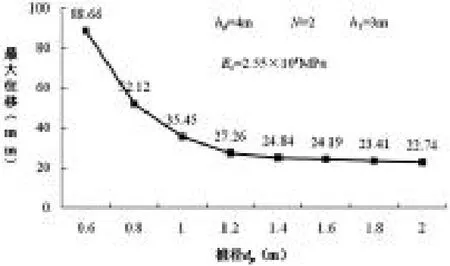
图1 最大位移与桩径关系曲线
1.2桩嵌固深度(如图2)
从上面的分析结果可以看出,最大位移值随嵌固深度hd的增大而逐渐减小。当嵌固深度小于7m时,最大位移值变化较为显著;而当嵌固深度大于7m时,最大位移值变化趋于平缓。由此说明,在支护结构安全稳定性有一定的保证的情况下,继续嵌固深度是无用的[3]。
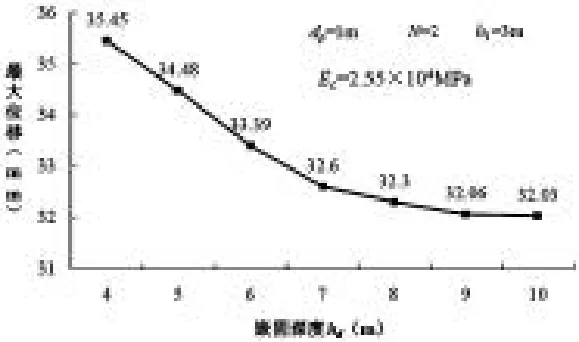
图2 最大位移与嵌固深度关系曲线
1.3支撑位置

图3 最大位移与支撑位置关系曲线
为了简化支撑位置对支护结构安全性影响的分析,设定第一道支撑和第二道支撑的间距为4m。依图3所示,最大位移值随支撑位置hi的变化不是单调变化,而是存在一个极值[4]。
1.4混凝土强度等级

图4 最大位移与混凝土强度值关系曲线
依图4所示,最大位移值随混凝土强度值Ec的不断增大而逐渐减小[4]。由此说明混凝土强度值也同样存在这样一个临界值,超出这个值,支护结构的安全稳定性不会明显提高,增加的只有造价而已[6]。
2 优化设计目标函数的数学描述
对于排桩支护结构,其造价一般包括桩体造、锚杆、内支撑造价以及施工造价等[7]。选取桩、锚杆材料造价为目标函数,可分别表示为:
2.1支撑结构为锚杆

2.2支撑结构为内支撑

式中:N为锚杆层数;Li为各层锚杆长度;As为配筋面积;Cs为排桩钢筋每kg造价;dp为桩径;Cct为混凝土每立方米造价;Lg为围护结构深度(Lg=基坑深度H+嵌固深度hd);Lg为基坑周长;Sh为锚杆水平间距;dp为锚杆直径;D为锚杆孔径;Ca为锚杆每立方米造价;Cm为砂浆每立方米造价;Cct为混凝土每立方米造价。
3 主要约束条件分析
3.1设计变量约束
设计变量的约束条件:
桩径dp:0.6~2.0m(钻孔灌注桩:0.6~1.2m,其它为0.6~2.0m);桩间距Sh:(1~3)dp;
混凝土等级:C20、C25、C30、C35、C40、C40、C50;
支撑道数:单支撑;双支撑;三支撑;四支撑;
支撑位置:

lf为第一层锚杆的自由端长度,ln为第一层锚杆的锚固端长度,θ为第一层锚杆的倾角,三者均为用户输入。
第二支点hb:ha+2≤hb≤ha+4且hb≤H-0.5
第三支点hc:hb+2≤hc≤hb+4且hc≤H-0.5
嵌固深度:0.2H≤hd≤0.6H。
3.2变量一致性约束
为了保证土体的自稳,最大桩间距应该满足下式:

其中θ=45°+φ/2,φ内摩擦角。
3.3设计准则约束
为了保证深基坑安全稳定性和一定使用功能,还必须满足一些设计准则约束。
3.3.1强度约束
桩身必须满足一定强度要求,以保证其不发生破坏,强度约束的表达式为:

式中:K为桩配筋安全系数;fcm为混凝土抗压强度;A为桩截面面积;α为受压区混凝土截面面积的圆心角与2π的比值;fy为钢筋抗拉强度;As为纵向钢筋总截面面积;ds纵向钢筋围成圆的半径;αt为受拉钢筋截面面积与总钢筋截面面积的比值[8]。

图5 沿周边均匀配筋的圆形截面
3.3.2变形约束
排桩支护结构最大水平位移应符合下式要求[i]:
g2(X)=δ-[δ]
式中:δ为支护桩的最大水平位移;[δ]为支护桩变形限制。
3.3.3排桩支护的整体稳定性约束
嵌固深度按整体稳定性条件圆弧滑动简单条分法计算确定,其公式为:
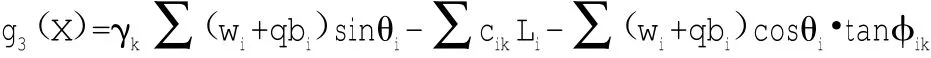
式中:γk为整体滑动分项系数,可取1.3;wi为第i分条土重;bi为第i分条宽度;cik为第i分条滑动面粘聚力;φik为第i分条滑动面内摩擦角;θi为第i分条滑动面中点切线与水平面夹角。
4 工程实例
某项目支护方案为:
(1)支护方案:护坡桩+5道预应力锚杆;
(2)设计支护高度:24.80m(实际施工以自然地面为顶标高);
(3)2-2剖面护坡桩桩径为φ1000mm,桩间距为1800mm;桩顶设计标高为-0.00m,桩底设计标高为-30.80m,嵌固深度6m,桩顶设置一道钢筋混凝土连梁,连梁断面尺寸为1000mm×600mm,护坡桩共190根,护坡桩、连梁混凝土强度C25,如表1、图6。
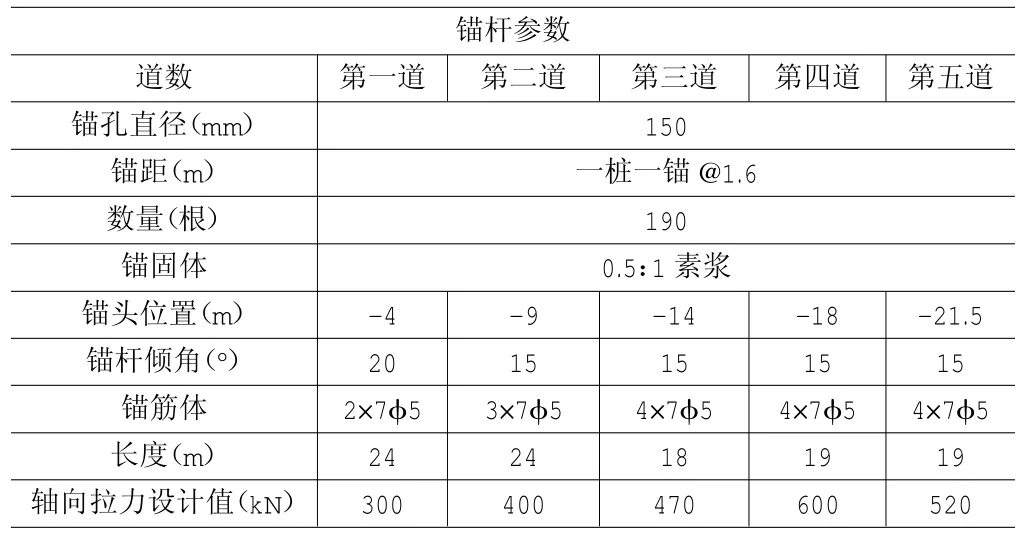
表1 2-2段支护结构设计表
采用作者编制的《深基坑优化设计软件V1.0》对该排桩支护结构进行优化,优化结果如表2。
5 结论
本文根据敏感性分析的结果,选择对优化结果影响显著的设计变量,并主要约束条件进行了归纳,确定以综合造价为优化目标的最终优化目标函数,从而建立了深基坑排桩支护结构优化设计数学模型。
[1]张海涛.深基坑支护设计与施工方案优化研究[D].武汉大学博士论文,2004.
[2]张霞.预应力锚杆格构梁的改进计算方法研究及优化设计研究[D].青岛理工大学硕士论文,2011.
[3]林义锋.基于遗传算法的排桩式锚杆挡墙优化设计[D].重庆大学硕士论文,2010.
[4]王辉,丁敏,喻诗淇.信息熵与FAHP耦合评价模型在深基坑支护方案优选中的应用[J].建筑结构,2011(S2):426~429.
[5]王俊生.改进遗传算法的基坑支护结构优化设计研究[D].武汉理工大学硕士学位论文,2004.
[6]周东.基坑支护工程遗传优化设计研究[D].广西大学博士论文,2002.
[7]侯公羽,弭尚银,杨春峰.进化策略及其改进算法在深基坑支护优化设计中的应用研究[J].岩土力学,2008,29(5):1222~1226.
[8]秦四清.深基坑工程优化设计[M].北京:地震出版社,1998.
[9]许小健,钱德玲.基于遗传算法的排桩支护结构优化设计[J].合肥工业大学学报(自然科学版),2007,30(11):1516~1519.

图6 支护结构型式图

表2 优化设计结果的对比
TU476
A
1673-0038(2015)38-0293-03
2015-9-7
丁敏(1983-),男,博士研究生,主要从事岩土力学、基坑优化等方面的研究。
