自动化立体仓库入库货位优化研究
2015-11-03山西中北大学机械与动力工程学院姚贝贝刘永姜王洋
山西中北大学机械与动力工程学院 姚贝贝 刘永姜 王洋
自动化立体仓库入库货位优化研究
山西中北大学机械与动力工程学院姚贝贝刘永姜王洋
为提高自动化立体仓库的运行效率,本文重点研究了固定货架系统中入库货物的储位优化问题 ,建立了储位优化的数学模型,采用一种改进的遗传算法进行求解。该算法在基本遗传算法的基础上,针对遗传算法中局部寻优能力不足的缺陷,引入一种“进化逆转算子”。通过实例仿真,优化后的结果表明,在储位优化方面显著提高了货架的稳定性,并且提高了货物的出入库效率。
自动化立体仓库;固定货架;储位优化;改进遗传算法
引言
自动化立体仓库是现代物流、仓储、自动化与计算机技术高度集成的产物,它集存储、输送、分发、管理等功能于一体,具有存储量大、占地面积小、节省人力、作业快速准确等优点,是现代物流的重要环节[1]。自动化立体仓库以巷道堆垛机来存取货物,通过周围的装卸搬运设备,自动进行出入库存取作业,提高仓库的利用率,节省了人力,降低了成本,提高了仓库的工作效率[2]。
如何对入库货物的货位进行科学有效的分配是提高货架存取率的关键,货位分配和进出库调度管理的合理安排将能使货架受力良好,同时可以减少堆垛机的工作量[3]。拣选作业优化的要求是合理确定拣选顺序,使拣选作业运行路径最短[4]。因此,通过研究自动化立体仓库调度的优化管理,来提高运行效率及加快仓储作业,对于方便企业仓库管理和增加企业的竞争优势具有重大的应用价值和现实意义[5]。针对自动化立体仓库实际运行模式,寻找收敛性能满足实时要求、收敛速度快的遗传算法,实现对自动化立体仓库的储位优化,具有重要的实际意义和理论价值[6]。
1 储位优化模型的建立
假设立体仓库有a排固定货架,每一排有b列、c层。自定义离出入库口最近的一排为第1排,且离出入库口最近的列为第1列,货架的最底层为第1层。假设该立体仓库可储存不同尺寸,不同重量,不同类型的货物。用pi表示第i种货物的周转率,mi表示第i种货物的质量,储位的单元格长度为L0,这里假设储位长宽高都是L0。
在建立储位优化模型前,提出如下假设:
(1)所有货物类型已知,不同货物形状和体积一样,但质量不同。并假设所建模型中储位单元格长宽高一样,巷道的宽度忽略不计。
(2)为了便于计算,只考虑叉车将货物由入库口送至货架上所消耗的时间。
(3)假设各个货架上托盘尺寸是一致的,不同的是托盘上所储存货物的质量。
按照做出的假设,取坐标为(x,y,z)的储位,且用(0,0,0)表示出入库口的位置坐标,则该货物由出入库口移动到储位的总距离为:

该货物移动到储位所消耗的时间为:

考虑到货物的出入库周转率,需要在离出入库口较近的位置放置周转率高的货物。则坐标为(x,y,z)储位上存储的货物在某个周期内的出入库过程中实际消耗时间可表示为:

最终建立的目标函数如下:

考虑到货架的稳定性,得出如下的目标函数:
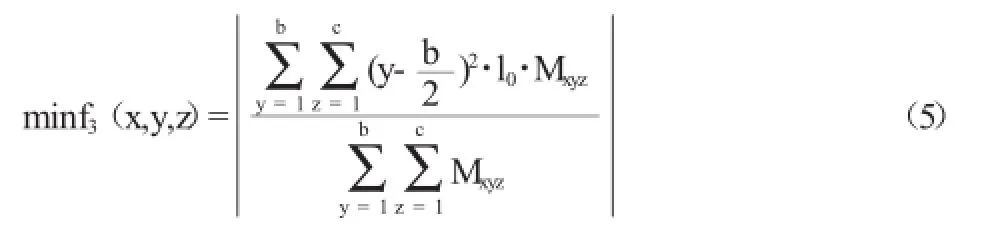
则最终得到的储位优化数学模型为:

模型中的变量:
Pxyz为储位(x,y,z)存储货物的周转率,为已知量;
l0为储位单元格的长度,为已知量;
Mxyz为储位(x,y,z)存储货物的质量,为已知量;
vx,vy,vz分别为叉车在X轴,Y轴,Z轴方向上的移动速度,为已知量;
a,b,c分别为立体仓库货架的排数、列数和层数,为已知量。
2 求解储位优化问题
货物入库时,若不按照一定的规则而随机进行存储,会使得入库时间长效率低下,且货架的稳定性无法保证,因此使用遗传算法进行优化,可有效改善这方面的问题。遗传算法是一种具有“生成+检测”迭代过程的随机搜索算法[7],改进遗传算法求解的过程如下。
2.1进行染色体编码
采用整数排列编码方式。用每个货位点的坐标来表示一个基因位,将一条染色体划分为M段,则表示在这个区域内可存储M种货物。
假设选择的优化区域中有五件货物,将编号为1~5的货物分别储存在(1,9,3),(2,5,4),(3,11,1),(1,13,5),(3,7,3)的储位上。则该染色体“19325431111135373”就代表了一个可行解,构成了一种储位指派方案。
2.2确定适应度函数
目标函数是求最小值,适应度函数为目标函数的倒数,由于该模型为多目标规划,采用简单加权和方法进行求解,因此,该模型对应的适应度函数可表示为:

m,n的取值视具体情况而定,且m+n=1。
2.3进行选择操作
以一定概率从旧群体中选择个体到新群里中,这里采用高级选择函数select,并调用低级选择函数sus,且在选择操作中引入代沟ggap,使得部分优良种群中的个体直接遗传到下一代。
2.4进行交叉操作
交叉算子是遗传算法中种群产生新个体的主要方法,其是指两个父代个体的结构加以替代重组而生成新个体的操作[9],采用部分交叉映射,两两分组后将父代样本按以下方式重组(假设每一个父代个体有15个基因)。
产生两个[1,5]区间内的随机数r1和r2,对由这两个数确定的位置进行交叉,例如r1=2和r2=3。
19325431111135373
21252361412142167
交叉后为:
1932361411135373
212525431112142167
2.5进行变异操作
随机选取两个点,将其对换位置。产生两个[1,5]范围内的随机整数r1和r2,确定两个位置,将其对换位置,如r1=2,r2=3。
19325431111135373
变异后为:
19331112541135373
2.6进化逆转操作
这里逆转算子具有单方向性,即只有经过逆转后,适应度值有提高的才接受下来,否则逆转无效[9]。产生两个[1,5]范围内的随机整数r1和r2,确定两个位置,将其对换位置,如r1=2,r2=4。
19331112541135373
进化逆转后为:
19311352543111373
2.7算子终止准则
通过对父代种群中的个体进行适应度值的计算,选择出适应度值大的个体进入下一代,然后进行交叉、变异和进化逆转操作,并不断循环这个操作,通过设定循环条件来判断是否满足最大遗传代数,不满足则继续进行适应度值的计算,否则结束遗传算法。
3 仿真实验及结果分析
以某个自动化立体仓库为例,将入库货位参数设置如表1。

表1 基本参数
现随机产生15种入库货物,其初始存储方案如表2所示。

表2 货物初始存储方案
在该优化模型中,通过综合考虑,对于该多目标规划遗传算法采用简单的加权和方法进行求解。将出入库效率和货架稳定性的权重系数分别定为0.6和0.4。优化后的结果如表3所示。将优化前和优化后的数据分别带入出入库效率和货架稳定性两个模型中,将两个方面所求的值进行对比得到表4。
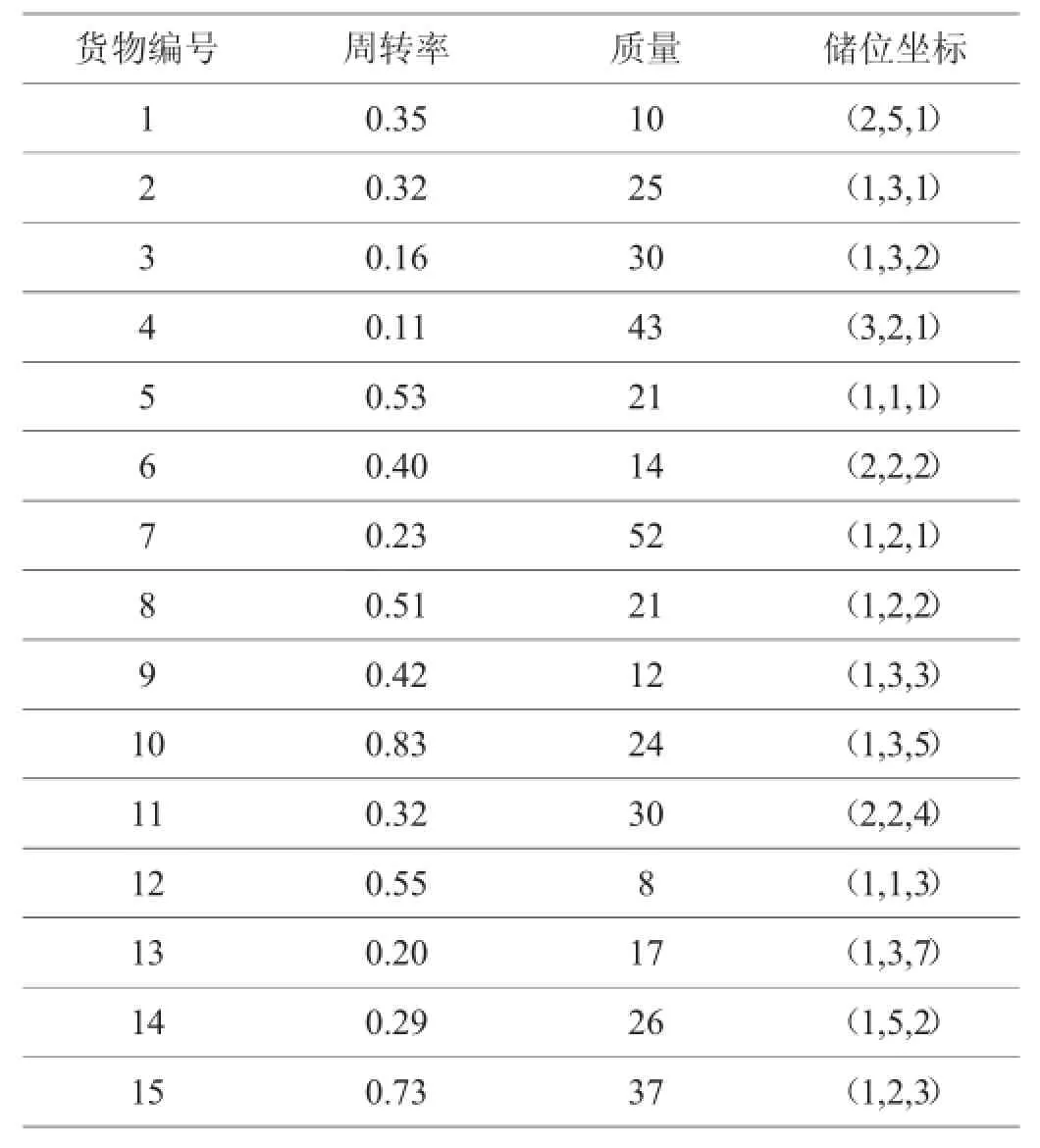
表3 货物优化后的存储方案
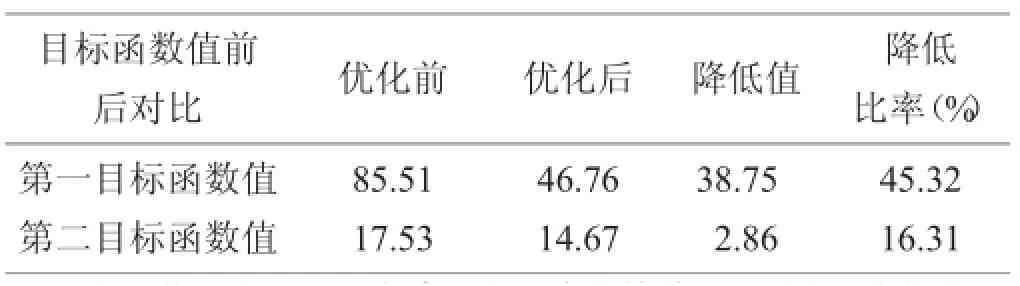
表4 优化前后两个目标函数值的对比
上述数据表明,通过采用改进遗传算法进行求解,货物的入库时间值降低了38.75,降低比率为45.32%;且货架的稳定性有了很大的改善,重心值降低了2.86,降低比率为16.31%,这既提高了货物的出入库效率,又提高了货架的稳定性,达到了全局优化的目的。
4 结论
(1)优化后的结果满足提高自动化立体仓库出入库效率和货架稳定性的要求,实现了货位的合理优化。
(2)改进遗传算法有清晰的求解思路和较好的收敛速度,因此,采用基于改进遗传算法的Matlab求解储位优化问题具有很高的实用价值,可有效避免因随机存储而造成的出入库效率低下、货架不稳定问题。
[1]宗晓萍,齐兴敏,王培光,朱玲玲.自动化立体仓库拣选作业优化研究[J].企业物流,2014(3):403-405.
[2]刘卉,李新,黄杨波.自动化立体仓库固定货架货位的优化研究[J].计算机与信息技术,2009,31(2):247-248.
[3]吴钟鸣,卢军锋,智淑亚.自动化立体仓库货位优化研究[J].装备制造技术,2011(12):23-25.
[4]柳赛男,柯映林,李江雄等.基于调度策略的自动化仓库系统优化问题研究 [J].计算机集成与制造技术,2006(9):1438-1443.
[5]云中,孙小明,潘尔顺.立体仓库库位号与堆垛机运作效率关系的探讨[J].工业工程与管理,2000(6):29-33.
[6]庞龙,陆金桂.基于蚁群遗传算法的自动化体仓库拣选路径优化[J].计算机工程与科学,2012,34(3):148-151.
[7]代桂平,王勇,侯亚荣.基于遗传算法的TSP问题求解算法及其系统[J].微计算机信息,2010,(4):15-19.
[8]DukicGoran,OluicCedomir.Order-pickingroutingpolicies:Simpleheuristicsadvancedheuristicoroptimalalgorithm[J].Journalof MechanicalEngineering.2004,50(11):530-535
[9]雷英杰,张善文,李续武等.MATLAB遗传算法工具箱及应用[M].西安:电子科技大学出版社,2005:20-35.
