磁流变弹性体阻尼器的磁路优化及有限元分析
2015-11-03徐文娟王加有
徐文娟,王加有,张 赛
(黑龙江科技大学 工程训练与基础实验中心,哈尔滨 150022)
磁流变弹性体阻尼器的磁路优化及有限元分析
徐文娟,王加有,张赛
(黑龙江科技大学 工程训练与基础实验中心,哈尔滨 150022)
为优化磁流变弹性体MRE阻尼器的磁路性能,选取线圈、弹性体、导磁体等关键尺寸作为优化参数,应用ANSYS参数化语言APDL,对MRE阻尼器模型进行了优化设计,分析不同输入电流值对磁感应强度的影响。结果表明:磁流变弹性体中节点的最大磁感应强度从0.72 T增加到0.98 T;当线圈中通入0~2 A的控制电流时,随着电流值的增大,磁流变弹性体的磁感应强度不断增加并优先达到磁饱和;在输入最大控制电流2 A时,磁流变弹性体的磁感应强度达到饱和值0.8 T,比优化前的0.7 T增加了14.29%,磁滞效应得到有效发挥。
磁流变弹性体阻尼器;磁路参数;优化;有限元分析
0 引 言
磁流变弹性体作为一种新型的智能材料,具有刚度可控,性能稳定、响应速度快、可逆性好、无沉降以及无需考虑密封等特性。国内外相关研究表明,磁流变弹性体MRE非常适用于作为阻尼器中的吸振元件对振动进行控制[1-7],因此,磁流变弹性体阻尼器的研究和应用受到了越来越广泛地关注。
一直以来,国内外的研究人员设计的MRE阻尼器主要是基于剪切工作模式。然而LERNER[8]等人通过对基于不同工作模式的磁流变弹性体进行研究后认为,就磁流变弹性体本身而言,它在挤压工作模式下所发生的磁致效应比剪切工作模式更充分。因此,基于挤压工作模式的MRE阻尼器具有更好的减振和移频效果,近年来受到研究人员的重视。
考虑具体的应用环境及磁流变弹性体的性能,理想的MRE阻尼器其磁路应满足四方面要求:
(1)MRE阻尼器内部磁路必须闭合,且穿过磁流变弹性体的有效磁力线较多,漏磁少。
(2)当MRE阻尼器的线圈中通入控制电流时,磁流变弹性体部分应能够产生比较均匀的磁场,并且磁感应强度能够随着控制电流的增大而增大,以确保磁流变效应达到一个可观的调控范围,从而使阻尼器能产生需要的移频效果。
(3)磁路中磁饱和顺序合理,磁流变弹性体处磁动势最大,且优先达到磁饱和,以充分发挥磁流变弹性体的磁致效应。
(4)磁路结构紧凑,使阻尼器的外形结构和尺寸大小能够满足在实际使用中的安装要求。
为优化磁流变弹性体(MRE)阻尼器的磁路性能,笔者选取线圈、弹性体、导磁体等关键尺寸作为优化参数,应用ANSYS参数化语言APDL,对基于挤压模式设计的MRE阻尼器模型进行优化设计,并采用ANSYS软件进行电磁场仿真分析和不同输入电流值对磁感应强度的影响分析。
1 磁路分析
MRE阻尼器结构如图1所示[8]。
由图1可知,该MRE阻尼器的磁路主要由上导磁体、下导磁体、铁芯、线圈、磁流变弹性体、间隙和套筒组成。
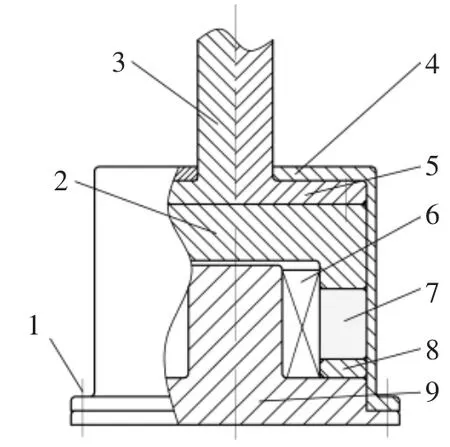
图1 挤压式MRE阻尼器结构Fig.1 Structure of magnetorheological damper based on extrusion modle
当线圈中通入最大允许电流I=2 A时,阻尼器中铁芯部分首先达到磁饱和,根据电磁场的饱和理论可知,当磁路中的某一部分达到磁饱和以后,即整个磁路出现了瓶颈,其他部分便不会再出现磁饱和的情况,若磁流变弹性体不能最先达到磁饱和,则其磁致效应不能达到最大,则阻尼器不能发挥最大的减振性能。
2 磁路优化
应用ANSYS参数化语言APDL编程,对MRE阻尼器的磁路进行优化[6-9],使铁芯和弹性体同时达到磁饱和或弹性体优先达到磁饱和,以优化该MRE阻尼器的性能。
2.1磁路结构简化与优化参数的设定
为方便参数化建模,建立MRE阻尼器的磁路结构。由于该MRE阻尼器的结构对称,其磁路简化后的结构如图2所示。
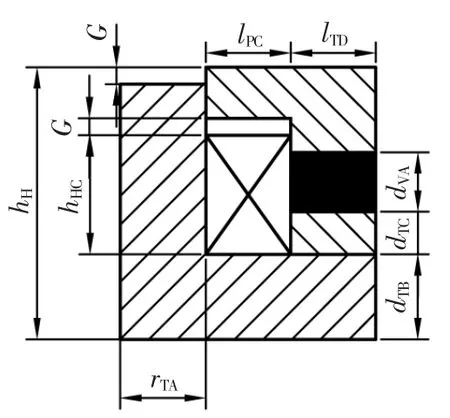
图2 MRE阻尼器磁路结构Fig.2 Structure of magnetorheological damper magnetic circuit
影响MRE阻尼器磁场强度的参数主要有铁芯半径、套筒的高度、上导磁体、下导磁体的高度及径向尺寸、线圈槽深、线圈高度等。在MRE阻尼器磁路优化中,为了使弹性体的面积具有一个合适的调节范围,文中将铁芯的半径rTA定为定值15 mm;为了保护铁芯处缠绕的线圈,将线圈上部与铁芯上部的空隙G设定为定值;弹性体的厚度dVA对整个磁路的磁阻变化影响较大,故也将其设定为定值,具体的初始参数设定见表1。磁流变弹性体的径向尺寸lTD、线圈高度hHC、线圈的径向尺寸lPC以及上、下导磁体的高度hTB设定为设计变量。将磁流变弹性体节点处的最大磁感应强度作为目标函数STRB,铁芯处的最大磁感应强度作为约束条件STRA。优化参数设置如表2所示。

表1 初始参数设定Table 1 Iinitial parameters mm

表2 优化参数设置Table 2 Optimization parameters
2.2磁路优化步骤
(1)分析文件的生成
分析文件的建立是运用ANSYS进行优化的关键,采用系统编辑器在分析文件中建立MRE阻尼器的参数化模型、网格划分、加载和求解以及提取结果并赋值给相应参数等命令。
(2)优化过程数据库参数的建立
通过读入建立的分析文件,在ANSYS中即可完成整个模型的数据库,便于定义优化变量。
(3)进入OPT,指定分析文件名
通过Command:/OPT命令直接进入优化处理。
(4)指定优化变量
指定MRE阻尼器模型的设计变量、状态变量和目标函数等,文中选定的设计变量为磁流变弹性体的径向尺寸rTD、线圈高度hHC、线圈的径向尺寸lPC以及上、下导磁体的高度dTB;状态变量为铁芯处的最大磁感应强度,以STRA表示。以磁流变弹性体节点处的最大磁感应强度作为目标函数STRB,具体的程序:
OPVAR,TB,DV,7e-3,15e-3,0.01e-3,
OPVAR,HC,DV,15e-3,30e-3,0.01e-3,
OPVAR,PC,DV,6e-3,15e-3,0.01e-3,
OPVAR,TD,DV,7e-3,12e-3,0.01e-3,
OPVAR,STRA,SV,0,2.5,0.01e-3,
OPVAR,STRB,OBJ,,,0.001。
(5)优化及结果输出
采用单步运行法与零阶方法相结合的方法,优化方法选定后,ANSYS就会通过优化方法进行优化运算,当后一步的优化结果小于前一步的优化结果,则目标函数收敛,优化结束。通过图形指示的方式显示目标函数、设计变量随迭代次数的变化情况,可用以下方法实现。
命令:PLVAROPT
GUI:Main Menu>Design Opt>Graphs/Tables
2.3磁路优化结果与分析
目标函数经过16次迭代得到设计变量的优化结果,为了使该MRE阻尼器便于加工,对各设计变量的尺寸进行圆整,圆整后dTB=9 mm,hHC=22 mm,lPC=6 mm,lTD=8 mm。
目标函数及各设计变量的迭代次数变化如图3所示,由图3可以看出,目标函数的值由原来的
0.72T增加到了0.98 T,增加了36.11%。同样磁流变弹性体的磁感应强度值也有较大地增加,各设计变量随目标函数收敛而逐渐平缓变化。通过优化前后结果的对比,优化后不仅减小了线圈的匝数,而且同样的励磁电流得到的磁感应强度值也比优化之前大,从而降低了能量的消耗,提高了MRE阻尼器的灵敏度与可控性。
优化前后的磁感应强度分布如图4、图5所示。由图4、图5可知,优化前磁流变弹性体的平均磁感应强度值为0.7 T,而经过优化之后的磁感应强度分布图有了明显改善,弹性体的平均磁感应强度值为0.8 T,增加了14.29%。铁芯的磁场分布更加均匀;磁流变弹性体没有出现磁饱和的情况,故弹性体的磁感应强度可以随着电流的增加而增加。同时,经过优化之后的结构体积降低了11.2%,阻尼器的磁路更加紧凑。
3 MRE阻尼器的电磁场仿真
对MRE阻尼器进行磁场仿真分析,得到MRE阻尼器的磁力线分布图、磁流密度分布图以及节点磁流密度分布图,对优化之后的MRE阻尼器的磁路结构进行综合评价。
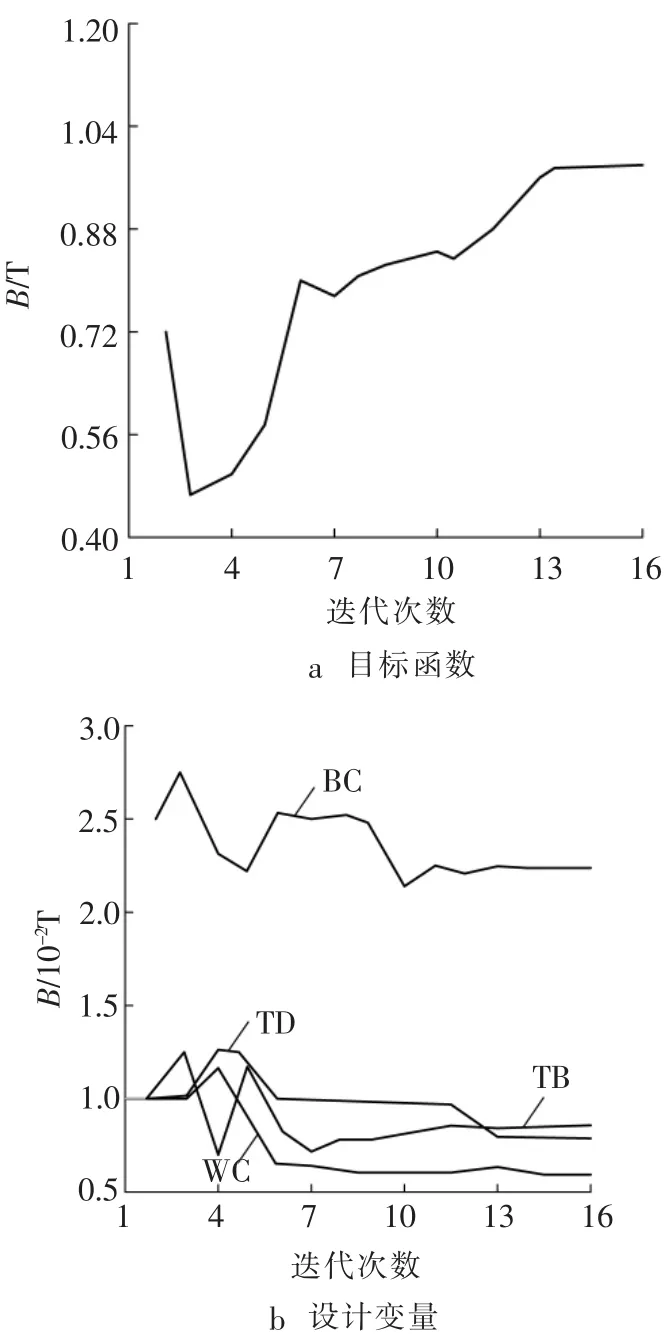
图3 优化参数Fig.3 Iterative map of parameter optimization
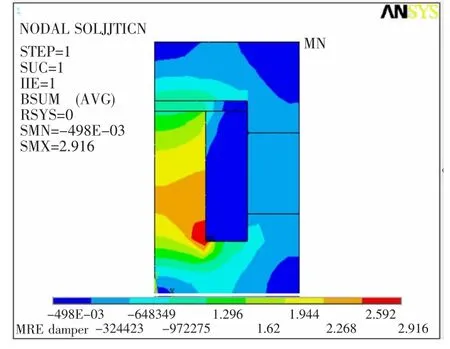
图4 优化前磁感应强度分布Fig.4 Magnetic induction intensity distribution before optimization
由于该MRE阻尼器是轴对称结构,故按2-D轴对称模型进行分析。由于线圈中施加的是稳态(DV)电流,故以通过的电流密度的形式输入。假设模型边缘边界与磁通量平行,用“flux parallel”施加模型的边缘边界条件。具体分析过程如下:
(1)创建物理环境
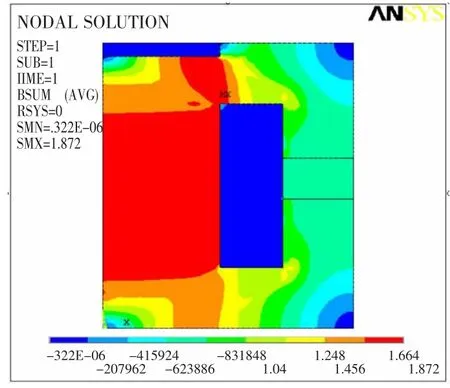
图5 优化后磁感应强度分布Fig.5 Magnetic induction intensity distribution after optimization
通过Main Menu>Preference弹出的菜单对话框,选中“Magnetic-Nodal”来创建分析过滤界面,并在使用菜单中完成工作标题的命名;在“Element Types”对话框中选定“PLANE13”单元类型,并将单元类型修改为对称结构。在“Define Material Model Behavior”对话框中完成材料属性的定义。
(2)建模、赋值及网格划分
在“Scalar Parameters”对话框中完成模型参数的输入,在“Creatangle by Dimension”矩形对话框中完成几何模型的创建,并通过“MeshTool”对话框对模型进行材料赋值和网格的划分。
(3)施加边界条件和载荷
在Apply JS on Elems电流密度对话框中,输入施加电流 “jdens/(0.01** 2)”,并在 Utility Menu> Select>Entities弹出的对话框中完成外围节点的选取,在On Nodes对话框中施加磁力线平行条件。
(4)求解
在Main Menu>Solution>Solve>Electromagnet>Static Analysis>Opt&Solv操作之后弹出的求解设置对话框中,直接点击“OK”开始求解运算,出现“Solution is done”对话框时,表示求解结束。
(5)后处理
在Main Menu>Genral Postproc>Plot Result中的选项对话框中,提取出磁力线、磁流密度等结果,如图6所示。
由图6a的MRE阻尼器中磁力线分布图可以看出,磁力线全部分布在模型中,无泄漏情况。铁芯、上导磁体、下导磁体、磁流变弹性体的磁力线分布均匀。由图6可以看出,MRE阻尼器中铁芯的磁感应强度最大,分布均匀,说明磁路中磁场利用率较高。磁路中磁流变弹性体首先达到磁饱和,达到了预期要求。
通过对优化后的MRE阻尼器的电磁场仿真分析可知,该MRE阻尼器的磁路结构得到了较大的改善;修正了磁路中的磁饱和顺序,同时提高了磁流变弹性体的磁感应强度值。

图6 MRE阻尼器仿真结果Fig.6 Simulation results of MRE damper
4 电流对MRE阻尼器的影响
MRE阻尼器主要是通过改变线圈中电流的大小来调节磁流变弹性体的磁感应强度,进而控制磁流变弹性体的刚度和阻尼。为了研究电流变化对MRE阻尼器的影响,文中对不同电流输入时磁流变弹性体的磁感应强度进行分析。这里只分析电流单因素的影响,故将其他参数设为定值;由于线圈中允许通入的最大电流值为2 A,因此,将电流分为0、0.25、0.5、0.75、1.0、1.25、1.5、1.75和 2 A等九种情况,其他参数保持不变,应用ANSYS的电磁场单元进行电磁场仿真,通过仿真结果提取出磁流变弹性体的磁感应强度值,如表3所示。为了进一步说明线圈中输入电流的大小对磁流变弹性体的影响,将不同输入电流值与磁流变弹性体的磁感应强度值同时输入到Matlab中进行处理,得到电流与磁感应强度值的数值曲线图,如图7所示。

表3 不同电流值时弹性体处的磁感应强度Table 3 Magnetic induction intensity under different current value
由图7可知,随着线圈中输入电流的不断加大,磁流变弹性体的磁感应强度值不断上升,当通入电流为2 A时,磁流变弹性体达到了磁饱和。说明整个磁路结构比较稳定,磁流变弹性体的磁场比较均匀,从而可以通过改变电流的大小来控制MRE阻尼器的刚度和阻尼。
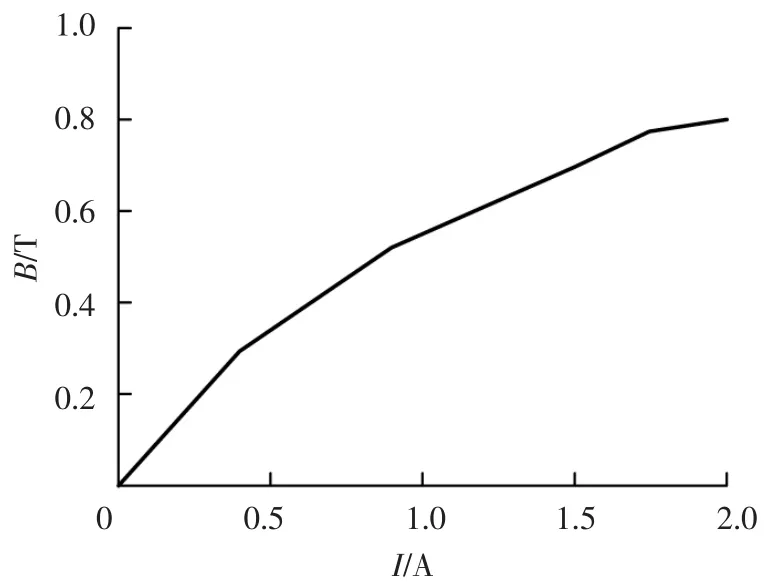
图7 磁感应强度值关系曲线Fig.7 Relationship about magnetic induction intensity values
通过对电流与磁感应强度变化曲线的分析可知,在通入1 A以内的电流时,磁流变弹性体的磁感应强度值上升比较快,说明磁流变弹性体的磁敏感度较高,在很小的磁场条件下就能发挥磁滞效应;但随着电流的不断加大,尤其是接近于饱和磁感应强度时,磁感应强度值的增速变缓,说明随着磁场的不断加大,磁流变弹性体的磁敏感度降低。
5 结 论
⑴优化后,该MRE阻尼器的磁路结构得到了较大的改善,铁芯、上导磁体、下导磁体、磁流变弹性体的磁力线分布更加均匀,说明磁路中磁场利用率较高。
⑵在线圈中输入最大控制电流2 A时,磁流变弹性体优先达到磁饱和,从而修正了磁路中的磁饱和顺序,且磁流变弹性体内的节点最大磁感应强度值比优化前提高了36.11%。
⑶当线圈中通入1 A以内的电流时,磁流变弹性体的磁感应强度值上升比较快,说明磁流变弹性体的磁敏感度较高,在很小的磁场条件下就能发挥磁致效应;但随着电流的不断加大,尤其是接近于饱和磁感应强度时,磁感应强度值的增速变缓,说明随着磁场的不断加大,磁流变弹性体的磁敏感度降低,这对MRE阻尼器的实际应用具有指导意义。
[1]龚兴龙,邓华夏,李剑锋,等.磁流变弹性体及其半主动吸振技术[J].中国科学技术大学学报,2007,37(10):1192-1203.
[2]吴平.磁流变弹性体智能器件研究[D].武汉:武汉理工大学,2011.
[3]王宇飞,何琳,杨雪,等.不着磁流变弹性体的研究现状及工程应用[J].材料科学与工程学报,2010,28(4):633-636.
[4]李季,赵韩,梁天也,等.新型磁流变弹性体隔振器关键技术[J].噪声与振动控制,2014,3(6):184-187.
[5]魏克湘,孟 光,夏 平,等.磁流变弹性体隔振器的设计与振动特性分析[J].机械工程学报.2011,47(11):69-74.
[6]刘春生,王庆华,李德根.镐型截齿截割阻力谱的分形特征与比能耗模型[J].煤炭学报,2015,40(11):2623-2628.
[7]叶伟强,曹宽宽,邓益民,等.磁流变弹性体汽车减振实验装置设计及实验研究[J].机械科学与技术,2011,30(6):1011-1015.
[8]LERNER A A,CUNEFARE K A.Performance of MRE-based vibration absorbers[J].Journal of Intelligent Material Systems and Structures,2008,19(5):551-563.
[9]XU W J,REN Z,WANG J Y,et.al.Magnetorheological elastomer damper design and finite element analysis[C]//Manufacturing and Engineering Technology,ICMET2014,2014:393-397.
(编辑李德根)
Magnetic circuit optimization and finite element analysis of MRE damper
XU Wenjuan,WANG Jiayou,ZHANG Sai
(Center for Engineering Training&Basic Experimentation,Heilongjiang University of Science& Technology,Harbin 150022,China)
This paper is an effort to optimize the magnetic circuit performance of MRE damper. The study achieves this optimization by choosing the key dimensions such as coil,elastomer and the guide magnet as the optimized parameters and using ANSYS parametric language APDL and thereby achieving an optimal design of MRE damper model;and performing the simulation analysis of the electromagnetic field and the influence of different input current values on the magnetic induction intensity.The results show that an increase from 0.72 T to 0.98 T takes place in the joints of the maximum magnetic induction intensity;connecting the coil to the control current of 0~2 A with an increased current value allows a constant increase in the magnetic induction intensity of the MRE and a consequent priority for magnetic saturation;inputting 2 A maximum control current results in the saturation value 0.8 T in the magnetic induction intensity of the magnetic rheological elastomer—a 14.29%increase over 0.7 T before the optimization,contributing to a significant hysteresis effect.
MRE damper;magnetic circuit parameter;optimization;finite element analysis
10.3969/j.issn.2095-7262.2015.06.021
TM141;TB535
2095-7262(2015)06-0681-05
A
2015-09-15
黑龙江省教育厅科学技术研究项目(12541732)
徐文娟(1963-),女,满族,辽宁省抚顺人,教授,硕士,研究方向:机械设计及理论,E-mail:xwj9707@sohu.com。
