V形网壳结构屋盖风荷载模拟分析

张俊杰，　袁文涛

（黑龙江科技大学 建筑工程学院，哈尔滨 150022）

V形网壳结构屋盖风荷载模拟分析

张俊杰，袁文涛

（黑龙江科技大学 建筑工程学院，哈尔滨 150022）

为研究V形网壳结构屋盖的风压分布规律，应用ANSYS-CFX软件对该结构进行风荷载数值模拟。对V形网壳结构屋盖进行实体建模，选取计算流域，进行网格划分，设定边界条件，并选取SST湍流模型对该结构进行数值模拟计算，分析V形网壳结构屋盖分别在0°、45°和90°风向角下的风压分布规律。结果表明：45°为该结构最不利风向角；由于45°和90°风向角下的结构表面整体负压值较大，所以应着重验算45°和90°风向角的局部负压和整体负压；不论风向角怎样变化，风吸力是此屋盖结构的主要荷载，其最大值一般出现在迎风结构面的边缘，结构边缘处风压梯度变化较大，屋盖V形折点区域局部风压较缓端局部风压大。

V形网壳结构；屋盖风压分布规律；风荷载；网格划分；湍流模型；数值模拟

0　引　言

随着社会的进步和科学技术的发展，传统的屋盖形式已不能满足人们对建筑结构功能的使用要求，因此，出现了许多新型的屋顶结构形式［1］。风荷载是屋顶结构的控制荷载，我国现行的GB50009—2012《建筑结构荷载规范》［2］中，只列出了一些常见结构形式屋盖的风荷载体型系数，对于一般性的复杂体型结构还需要做深入分析。风洞实验是研究结构风载的重要手段，它能够在一定程度上还原真实环境中风荷载对结构物的影响。但风洞实验持续时间较长、资金消耗较大，并且无法提供相应的流场信息。随着计算机技术和流体力学的迅速发展，以流体动力学为基础的数值模拟方法克服了风洞实验的不足。数值模拟方法［3］是利用计算机技术模拟建筑物周围风场，计算结构风压的一种方法。计算风工程也被称为数值风洞［4］，其研究成果需要在一些假设的基础上完成。湍流模型用来模拟风绕建筑物的流动形式，其具体形式是流体在流域内随时间与空间的不断波动，目前，常用的几种湍流模型在风荷载模拟中都存在一些缺陷，可以说计算风工程技术的水平高低与湍流模型技术的水平密不可分［5］。同时，在数值模拟过程中，模拟方法、网格划分及计算流域等也对模拟结果有直接的影响［6］。总体来说，利用数值模拟方法研究风载荷对屋顶结构的影响具有重要意义。

1　模型建立与计算流域选取

数值模拟第一步建立建筑模型和流体域模型。首先，采用Design Modeler软件进行实体建模，模型为V形网壳结构屋盖形式，模型长60 m，宽56 m，高15 m。接着，进行计算流域的选取，计算流域的尺寸与数值模拟精度关系密切，计算流域的尺寸太小，会影响结构表面风压分布；尺寸选取过大，则会增加计算网格数量，从而导致资源的浪费，并且影响计算精度的提升［7］。一般的计算流域选取原则［8］如下：设模拟实体对象的高度为h，对于高度较低的建筑物，风场流动的主要形式为顶面绕流，流域的入口一般设定在离结构物4h～5h的位置。流域的出口边界，需要保证尾流充分发展，否则会有回流，计算不收敛。但是由于结构体远端网格体积大，湍流能耗散较快且对入口端影响较小，因此，在进行建筑物风荷载模拟时，可以将出口与结构体之间距离适当缩短，综合以上两点出口边界一般设定在离建筑物背风面2h～3h的位置。计算流域侧边缘与结构物之间的距离应为3h～4h，阻塞率应小于3%。文中模拟对象为低矮建筑结构，流域大小选取按上述原则进行。此外，模型和流域均为对称结构，在建模时只建立了几何模型的一半区域，具体尺寸，L=210 m，H=68 m，W=94 m，所建模型及流域选取如图1所示。

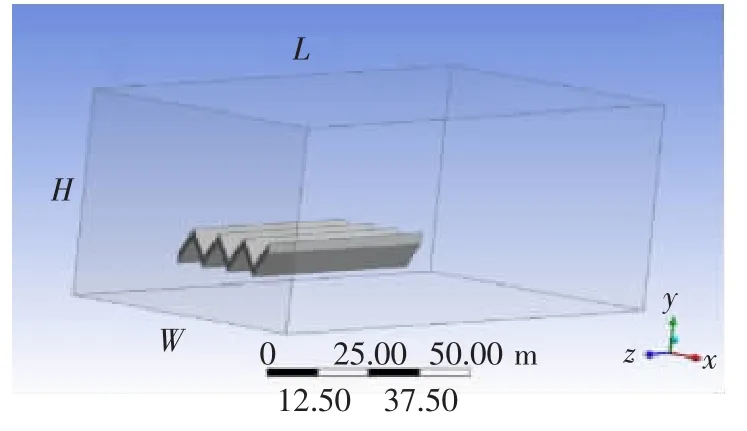
图1　屋盖几何模型与计算流域Fig.1　Roof geometry model and calculation of basin

2　计算网格划分

数值模拟第二步进行网格划分。网格是应用有限元的思想来离散连续的计算区域，并将连续的计算区域划分为若干个子区域进行计算，同时确定子区域中的节点［9］。网格一般从其大小和质量两方面判断其优劣程度。较差的网格划分会导致模拟计算无法进行或中止模拟计算，而较好的网格划分可以使计算结果的正确性和精确性得到有效提高。

文中采用 ANSYS12.0中的网格划分软件ICEM进行划分，软件中网格有四面体和六面体两种形式，如图2所示。

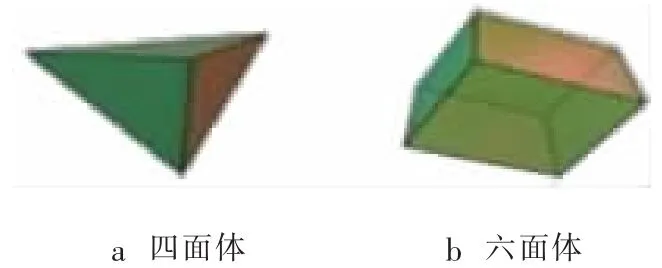
图2　ICEM中的网格形式Fig.2　Grid form in ICEM

计算精度的控制因素之一是网格的质量，网格的质量主要是网格类型的选取。网格分为结构化和非结构化网格两种，结构化网格［10］是指每个网格区域中的节点有相同的毗邻单元。与结构化网格的定义相比，非结构化网格［11］是指每个网格区域中的节点不具有相同的毗邻单元，并且采用随机数据生成网格节点，即不同的网格划分区域中的节点相连的网格数目也不同。一般体型的建筑结构常采用结构化网格划分建筑物，而体型复杂的常采用非结构化网格。结构化网格可以很容易地实现区域的边界拟合，适于流体和表面应力集中等方面的计算，网格生成的速度快、质量好，但适用的范围比较窄，对求解复杂区域适应性差。非结构网格生成过程中采用一定的准则进行优化判断，因而能生成高质量的网格，容易控制网格大小和节点密度，采用随机的数据结构有利于进行网格自适应。但在满足同样流场计算条件下，它产生的网格数量要比结构网格大得多。

此外，网格的数量在划分网格中是另一个重要的控制因素，网格数量过多会导致模拟计算时间过长，造成不必要的浪费；数量少则会使计算结果不够精确。因此，对远离建筑物的流体计算区域可以适当减少网格的数量，对于建筑结构表面区域及其相邻近的计算流域需要进行网格的加密。

针对模拟实体结构，综合考虑以上因素，采用四面体非结构网格对V形网壳结构屋盖进行网格划分。结构体及计算域采用四面体网格（个别位置采用楔形体或锥体），面网格采用三角形网格，运用ICEM网格编辑中的adjust mesh density对V形网壳屋盖结构进行加密处理，从而得到10 486个节点和66 954个体单元。具体划分情况如图3所示。

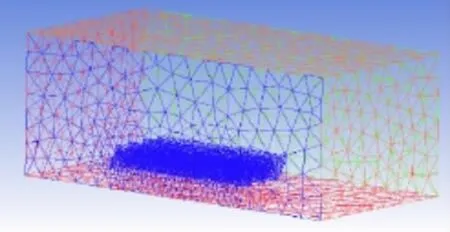
图3　V形网壳结构屋盖网格划分Fig.3　Mesh structure of V-shaped dome

3　边界条件与湍流模型

将已划分好网格的流体模型在CFX前处理中定义为流体域。流体域设定完成后，设定边界条件，边界类型包括入口边界、出口边界、无滑移壁面边界和自由滑移壁面边界。

3.1入口边界

入口边界条件的设定是在流域的入口处指定模拟所需的各类参数，设定入口面边界类型为inlet，并设置相关参数。入口边界为设定风场的平均速度和用于模拟的湍流模型。在设定边界信息时，空气模型选用理想不可压缩气体模型，质量与动量选定Normal Speed，速度值设定为15 m/s。

3.2出口边界

出口边界条件的设定是在流域的出口处指定模拟所需的各类参数，设定出口面边界类型为outlet，并设置相关参数。使用outlet出口边界是认为流体在出口处的流动情况由流域内部向外部发展得到，即认为流体完全发展，对上游流体流动没有影响。考虑到风场在出口边界需要充分发展，设置在垂直于出口面方向上的变量梯度值为零。设定出口边界处质量与动量为Static Pressure，相对压强值为0 Pa。

3.3壁面边界条件

壁面边界条件的设定是在流域的各侧面（非入口面与出口面）指定模拟各面的边界类型并设置相关参数，壁面边界条件类型为wall，其类型划分为无滑移的壁面条件 （No slip wall）和自由滑移壁面条件（Free slip）。计算模型为对称结构，建模时只需建立其对称的一半区域；将结构模型的表面和计算域底面设定为无滑移的壁面条件，即认为流体在近壁面处的速度为零；为了模拟大气边界层条件，将计算域顶部和一侧设定为自由滑移的壁面条件，即认为近壁面处的流体流动不受壁面边界的影响。

3.4湍流模型

湍流模型用来模拟风绕建筑物的流动形式，其具体过程是流体在流域内随时间与空间的不断波动［12］。湍流形式往往取决于流体本身的性质，如果流体本身的惯性力大于黏性力，湍流就会发生，常用雷诺数［13］来表明湍流的状态，具体表达为

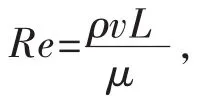
式中：ρ——流体的密度；

μ——流体的黏度；

v——流体表征速度；

L——流体表征长度。

雷诺数较小，表明流体的黏性力大于惯性力时，流体内各质点平行于流域内壁进行规则的流动，此时流体为层流状态；雷诺数较大，表明流体的惯性力大于黏性力，流体内各质点的流动状态为杂乱的无规则流动，此时流体为紊流状态。湍流模型的发展是以确定影响湍流运动规律的因素以及根据湍流运动规律寻找附加条件和关系式为基础的。由于在模拟过程中很多风场环境不能表述清晰，所以，为了还原真实的风场环境，对湍流模型的运用显得尤为重要。

常用的湍流模型有标准k-ε模型和SST（Shear Stress Transport）两种。在计算复杂湍流场时，标准kε模型不能模拟出风场的真实环境，风绕建筑物流动为复杂的绕流场，因此，建筑计算风工程中不宜采用标准k-ε模型。SST模型能较好地模拟复杂湍流场，并且适用于复杂体型结构的模拟。根据模拟环境，采用SST模型进行计算。

4　结果与分析

由于气流绕流特性的不同会造成屋盖表面风压分布的差异，所以在此类结构的实际设计过程中，需要分析不同来流方向对屋盖风荷载分布的影响。模型为对称结构，只选取具有代表性的0°，45°和90°三种风向角，对V形网壳结构屋盖进行风荷载数值模拟，模拟结果如图4所示。

图4　不同风向角下的风压分布Fig.4　Pressure distribution under different wind angles

由图4可知，0°风向角为风的流向垂直于屋盖前缘，风流在屋盖前缘分离，此时，屋盖表面整体负压值偏小，最大风吸值出现在迎风屋面边缘的V形最低折点处，而随屋盖坡度上升风吸值逐渐减小，屋盖前缘的风压梯度变化较大。45°风向角时，与0°风向角不同的是最大风吸值出现在迎风屋面边缘的V形最高折点附近，在远离屋盖前缘的中部，风压出现正值。90°风向角时，与上两种风向角不同的是V形屋盖后边缘出现了最大风吸值。

5　结　论

（1）根据三种风向角下风压分布对比，45°风向角下结构出现最大负压值，并且结构边缘风压梯度变化最大，因此45°为最不利风向角。

（2）45°和90°风向角下的结构表面整体负压值较大，因此，应着重验算45°和90°风向角的局部负压和整体负压。

（3）不论风向角怎样变化，风吸力是该屋盖结构的主要荷载，其最大值一般出现在迎风结构面的边缘，各风向角下结构迎风面周边区域的局部风压较其他区域大，屋盖V形折点区域局部风压较缓端局部风压大。在实际工程的设计中，V形折点处风荷载的验算应重点考虑。

（4）所建模型未考虑其自身变形，视为刚性模型。该研究避免了风洞实验的不足，具备模拟真实环境的能力，具有周期短、费用低的特点。

［1］塔尼娅·布罗屈克.屋顶构造［M］.北京:中国建筑工业出版社，2010：56－57.

［2］中华人民共和国住房和城乡建设部.GB50009—2012建筑结构荷载规范［S］.北京：中国建筑工业出版社，2012.

［3］孟兮.大跨度空间结构风荷载的数值模拟计算与分析［D］.北京：北京交通大学，2010：63－70.

［4］孙瑛.大跨度结构风荷载特性研究［D］.哈尔滨：哈尔滨工业大学，2007：27－42.

［5］姚志东.基于数值模拟方法的大跨度结构表面风荷载的计算与分析［D］.北京：北京交通大学，2008：36－47.

［6］吴迪，武岳，孙瑛，等.大跨度铁路站房屋盖结构风洞试验与等效静风荷载研究［J］.建筑结构学报，2011，33（1）：43-50.

［7］李鸿基.体育馆大跨度悬挑屋盖结构的风荷载数值模拟［D］.南宁：广西大学，2012：40-50.

［8］刘思为.大跨度空间结构风荷载数值模拟及风振响应研究［D］.西安：西南交通大学，2011：54-69.

［9］顾明，黄鹏，杨伟，等.上海铁路南站平均风荷载的风洞试验和数值模拟［J］.建筑结构学报，2004，25（5）：43-47.

［10］王莹.大跨度空间结构风荷载数值模拟研究［D］.天津:天津大学，2012：25-47.

［11］LILLY D K.Proposed modification of the Gemano subgrid-scale closure method［J］.Phys Fluid A，1992，4（3）：633-635.

［12］李雪丹.基于CFD技术建筑结构风荷载数值模拟研究［D］.广州:华南理工大学，2013：59-69.

［13］楼文娟，孙斌，卢旦，等.复杂型体悬挑屋盖风何载风洞试验与数值模拟［J］.建筑结构学报，2007，28（1）：107-112.

（编辑徐岩）

Numerical simulation analysis of wind load on V reticulated shell structure

ZHANG Junjie，YUAN Wentao
（School of Civil Engineering，Heilongjiang University of Science&Technology，Harbin 150022，China）

Thi s paper is directed at investigating the law underlying the distribution of wind pressure acting on roof with V-shaped reticulated shell by a numerical simulation of the wind load on this structure using ANSYS-CFX software.The numerical simulation is performed by selecting the grid and calculating the boundary conditions；using the SST turbulence model to provide the numerical simulation of the structure in study；and using the SST model to analyze the law behind the distribution of wind pressure on the shell roof，as in the case of various wind direction from 0-degree to 45-degree and 90-degree.The study shows that 45 degrees is the most unfavorable wind direction for the structure；the greater overall negative pressure value of the structural surface under 45-degree and 90-degree wind direction dictates a focus on the checking calculation of the local negative pressure and negative pressure of the 45-and 90-degree wind direction；and despite any change in wind direction，the wind suction remains a main load acting on the roof structure，a load whose maximum value typically occurs in the windward structure edge subjected to a greater gradient change in wind pressure；produces a greater local wind pressure in V-shaped folded point area than in the gentler slope of roof structure.

V reticulated structure wind pressure distribution law；wind load；grid division；turbulence model；numerical simulation

10.3969/j.issn.2095-7262.2015.06.017

TU339

2095-7262（2015）06-0660-04

A

2015－10－09

张俊杰（1965-），女，黑龙江省哈尔滨人，副教授，硕士，研究方向:土木工程，E-mail:120611966@qq.com。