方形与圆形管道内多孔介质渗流的实验研究

章晓伟,　王海桥, 2,　陈世强, 2,　罗聪亮,　彭　莹

(1.湖南科技大学 能源与安全工程学院, 湖南 湘潭 411201;2.湖南科技大学 湖南省矿山通风与除尘装备工程技术研究中心, 湖南 湘潭 411201)



方形与圆形管道内多孔介质渗流的实验研究

章晓伟1,王海桥1, 2,陈世强1, 2,罗聪亮1,彭莹1

(1.湖南科技大学 能源与安全工程学院, 湖南 湘潭 411201;2.湖南科技大学 湖南省矿山通风与除尘装备工程技术研究中心, 湖南 湘潭 411201)

为了研究压差与填充物料堆积形态对多孔介质渗流流动的影响,进行方形与圆形管道陶粒填充渗流实验。利用自主搭建的实验装置,分别测定两组方形管道和两组圆形管道渗流压差与渗流速度。应用线性与非线性渗流理论,分析该四组实验数据,得到线性与非线性渗透率和非达西因子。结果表明:随着压差的增大,流动从线性逐渐过渡到非线性;随着填充密实程度的增加,非线性渗流渗透率变小,非达西因子变大。

多孔介质; 渗透率; 非线性流; 非达西因子

渗透率是多孔介质渗流中最重要的基本参数[1]。采用宏观流体力学理论和方法,雷树叶等[2-3]得出了颗粒填充多孔介质中渗透率与孔隙率和粒径之间的经验关系式。随着多孔介质堆积形态等条件的不同,多孔介质中孔隙率、渗透率和粒径之间的关系也会随之变化。至今,尚未见一个普适的关系式可以描述三者间的关系[4-5]。笔者利用自主搭建的实验装置,实测陶粒填充的方形与圆形管道流动参数,讨论线性与非线性渗流态下的渗透率和非达西因子。

1　实验系统与方法

为了对比陶粒填充方形与圆形管道多孔介质渗流情况,自主设计了多孔介质渗流实验系统，原理如图1所示。

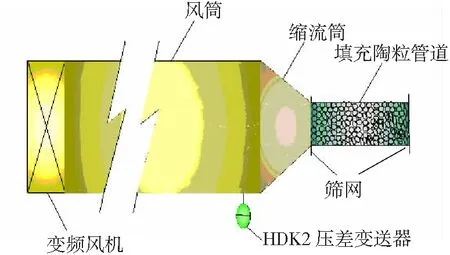
图1　空气渗流实验系统原理

实验采用变频风机,首先,将管道中填满陶粒,陶粒呈椭球形,长轴为39～42 mm,短轴为20～24 mm,管道两端用筛网封堵,将其用螺丝安装固定在缩流筒上。开启风机,待管道出口端风流稳定后,在管道出口端均匀选取九个点,用TSI9565P型风速计测量九个点的速度,取其平均值作为空气渗流的速度。由HDK2压差变送器自动记录下压力值;将风机的频率逐渐调高,依次测十组数据。然后,再将管道的陶粒倒出,在管道无填充陶粒的情况下,按照上述步骤,在相同的风机频率下依次测量十组数据。将两种状态相同风机频率下HDK2压差变送器测得的压力值依次相减,即得到在风机不同频率下多孔介质空气渗流的压差。由于变频风机转速比与频率比的非线性关系[6-7],所以，为尽量保证风机每次变频风量等量递增,风机调频频次依次为25%、30%、40%、45%、50%、60%、70%、75%、85%、90%。根据实验方法,测量四组管道的渗流压差与渗流流速,其中，圆形管直径D分别为200和400 mm两组,方形管边长L分别为200和400 mm两组,各组管道长度均为2 m。

2　线性与非线性渗流理论

流体在多孔介质中渗流且为线性渗流时,渗流符合达西定律:

(1)

式中:v——渗流速度,m/s;

k——渗透率,m2;

Δp——渗流压差,Pa;

μ——流体动力黏性系数,Pa·s;

L1——管道长度,m。

当渗流中流体惯性力相比黏性力不能再被忽略时,多孔介质中渗流将进入非线性流阶段。此时,渗流不能作为线性流来处理,否则，误差就会偏大。非线性流的公式有多种形式,其中应用较广泛的一维非线性流方程[8]为

(2)

ρ——流体密度,kg/m3;

β——非达西流因子,m-1。

式(2)中,μ取1.86×10-5Pa·s。

3　实验数据与结果分析

3.1线性渗流的压差与渗透率

利用实验装置,分别测得各组实验渗流压差和渗流速度，如表1所示。

将表1中各组测得的渗流压差与渗流速度用达西定律进行分析,根据式(1)的线性流公式,分别计算出各组渗透率,如表2所示。

分析表2,可以得出,L200方形管与D200圆形管相比,前者渗流压差略微小于后者,但前者渗流速度却略微大于后者,表明方形管更有利于渗流发生。分析两组管道断面形状,方形管边缘各向与中心不等距,且四边交接处为直角,使得陶粒填充不饱满;圆形管边缘为圆滑的弧形,且边缘各向与圆心等距,相对于方形管,圆形管内试样分布更加均匀且饱满[9];由于圆形管内试样孔隙率低于方形管,所以空气在方形管内渗流比在圆形管内更容易,导致口径大小相同的管道中圆形管渗透率比方形管渗透率小。L400方形管与D400圆形管亦是如此。L200方形管与L400方形管相比,后者渗流压差与速度均增大,但渗透率却显著减小。这是因为当管道口径增大时,填充陶粒总重量增加,使得陶粒间挤压得更加严实,从而陶粒分布密实度增加,不利于渗流发生,导致渗透率减小;另外,当管道口径增大时,陶粒粒径与管径比减小,也会使陶粒分布密实度增大[10],不利于渗流发生，导致渗透率减小。不同管径的圆形管亦是如此。

表1实验测得的压差与渗流速度

Table 1Differential pressure and seepage velocity of measurements

L200方形管Δp/Paυ/m·s-1D200圆形管Δp/Paυ/m·s-1L400方形管Δp/Paυ/m·s-1D400圆形管Δp/Paυ/m·s-115.410.8416.380.7638.031.2840.151.2118.751.0820.810.9951.211.6353.111.5024.231.3927.171.2983.502.0986.431.9931.791.7535.851.63109.002.54114.232.3945.582.3750.612.24140.112.96145.982.8356.242.8263.322.67200.083.63207.743.4271.473.2778.533.12271.114.32281.264.1787.123.7295.203.58305.134.71317.124.48102.664.20112.454.04345.955.01364.354.83121.184.71132.184.53390.895.35409.125.21

表2达西定律下的压差与渗透率

Table 2Differential pressure and permeability applied by Darcy law

L200方形管Δp/Pak/10-5m2D200圆形管Δp/Pak/10-5m2L400方形管Δp/Pak/10-5m2D400圆形管Δp/Pak/10-5m215.410.202716.380.172638.030.125240.150.112118.750.214320.810.176949.41*0.122752.76*0.110724.23*0.213427.17*0.176684.610.091986.430.085731.790.195435.850.1618109.000.0859114.230.077845.580.184450.610.1565140.110.0786153.980.072156.240.179263.320.1539200.080.0675222.740.061271.470.163978.530.1454271.110.0593292.260.055187.120.153295.200.1359305.130.0574327.120.0525102.660.1522112.450.1323345.950.0539368.350.0493121.180.1394132.180.1235390.890.0509415.120.0473

注:“*”为线性与非线性渗流压差临界点,且等于该值仍看成线性渗流的压差。

仔细观察各组渗透率,可以发现渗透率存在一个“跳跃”阶段,如图2所示。

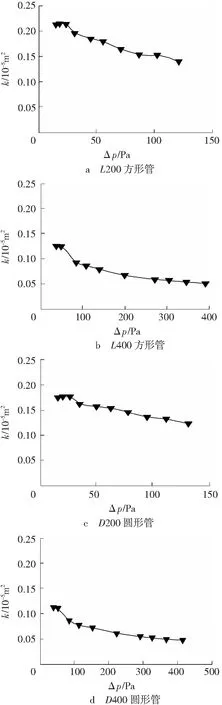
图2　管压差与渗透率的关系

Fig. 2Relationship between differential pressure of pipe and permeability

方形管L200与圆形管D200渗透率中,前三组渗透率趋向稳定,到第四组渗透率下降明显,呈“跳跃”变化特征,且此后渗透率保持下降趋势,渗透率变化的“跳跃”特征在方形管L400与圆形管D400表现尤为明显。观察图2各组渗透率变化曲线可知,曲线初阶段渗透率几乎保持不变,即压差与流速成线性关系,随后渗透率较之前陡然下降,且往后测点渗透率均保持下降趋势,压差增幅与流速增幅的比值呈递减趋势,即压差与流速成非线性关系,显然,该阶段渗流已经进入非线性流状态。

3.2非线性渗流的渗透率与非达西因子

将各组非线性流区域的渗流压差与流速数据进行非线性流分析,非线性拟合的关系式按式(2)处理,得到如下各组拟合方程:

(3)

(4)

(5)

(6)

根据式(3)～(6),利用各项系数,计算得到各组非线性流区域的渗透率k和非达西因子β,如表3所示。

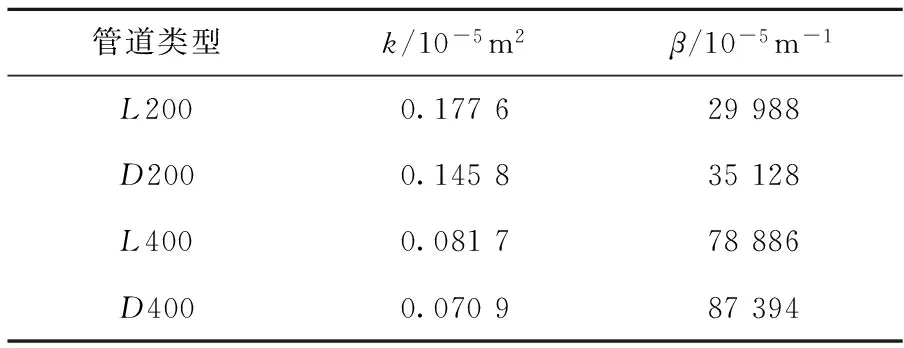
表3非线性渗流的渗透率与非达西因子

Table 3Permeability of nonlinear seepage and non Darcy factor

管道类型k/10-5m2β/10-5m-1L2000.177629988D2000.145835128L4000.081778886D4000.070987394

表3中,非线性渗流的渗透率依次递减,而非达西因子显著增加。对比表2与表3各组的渗透率,发现各组从线性流变成非线性流时,渗透率显著减小。分析认为,当渗流为非线性流时,流动相对线性流变得更加紊乱,使得流动压损非线性地增加,线性流流动难以维持,反应在渗透率的显著减小。

分别对比L200与D200的渗透率和L400与D400的渗透率,发现相同口径下方形管渗透率略微大于圆形管渗透率;分别对比L200与L400的渗透率和D200与D400的渗透率,发现随着管道口径的增大,渗透率显著减小。

4　结　论

(1)渗透率随着多孔介质堆积形态不同而变化。当陶粒分别填充在长度、口径相同而形状不同的管道内时,方形管的渗透率略微大于圆形管的渗透率;当陶粒分别填充在形状、长度相同而口径大小不同的管道内时,渗透率随着管道口径增大而显著减小。在非线性流阶段,非达西因子与渗透率成反比变化。

(2)线性流只在渗流的低流速阶段内才发生,随着压差与流速的增大,线性流状态便被破坏,转变为非线性流。

[1]LEI SHUYE, WANG BUXUAN. A practical seepage model for heat and mass transfer in porous media [C]//International symposium on transport phenomena in thermal engineering. New York: Begell House Inc, 1993: 221-226.

[2]ERGUN S. Fluid flow through packed columns[J]. Chemical Engineering Progress, 1952, 48(2): 89-94.

[3]雷树业, 王立群, 贾兰庆， 等. 颗粒床孔隙率与渗透率的关系[J]. 清华大学学报: 自然科学版, 1998, 38(5): 78-81.

[4]薛定谔. 多孔介质中的渗流物理[M]. 北京: 石油工业出版社, 1982.

[5]孙艾茵, 刘蜀知, 刘绘新. 石油工程概论[M]. 北京: 石油工业出版社, 2008.

[6]贾腾, 王海桥, 陈世强, 等. 矿用风机电机变频频率比与转速比的关系模型[J]. 黑龙江科技大学学报, 2014, 24(4): 397-400， 409.

[7]贾腾, 王海桥, 陈世强, 等. 固定频率下主通风机工频与变频运行时的对比实验研究[J]. 矿业工程研究, 2014, 29(4): 63-67.

[8]宋宜猛. 采空区分区渗流与煤自燃耦合规律研究[D]. 北京: 中国矿业大学, 2012.

[9]杨剑, 王劲, 步珊珊, 等. 颗粒有序堆积多孔介质对流换热实验研究[J]. 工程热物理学报, 2012, 33(5): 851-855.

[10]黄晚清, 陆阳, 何昌轩, 等. 刚性散粒体随机堆积的三维数值模拟[J]. 公路交通科技, 2006, 23(12): 21-24.

(编辑徐岩)

Comparison experiment on porous medium seepage flow in rectangle and circular pipes

ZHANGXiaowei1,WANGHaiqiao1, 2,CHENShiqiang1, 2,LUOCongliang1,PENGYing1

(1.School of Mining & Safety Engineering, Hunan University of Science & Technology, Xiangtan 411201, China; 2.Hunan Province Engineering Research Center of Mine Ventilation & Dust Removal Equipment, Hunan University of Science & Technology, Xiangtan 411201, China)

This paper is concerned with an experiment on the seepage flow fields in the rectangle and circular pipes with the ceramsite filling to study the effects of the differential pressure and the filling material accumulation morphology on the porous media seepage flow. This study does so by using independently designed experimental apparatus to perform the measurements of the differential pressures and velocities of the seepage flow in two sizes of the rectangle pipe and in two sizes of the circular pipe respectively, analyzing the data of four size pipes applying the linear and nonlinear seepage flow theory, and thereby deducing the linear, nonlinear permeability and non-Darcy factors from the data. The results show that the regime of seepage flow experiences a gradual transition from the linear to nonlinear due to the increase of differential pressure; and an increase in the filling compacting degree in a pipe results in a decrease in permeability of nonlinear seepage flow, but an increase in the non-Darcy factor.

porous media; permeability; nonlinear flow; non-Darcy factor

2015-08-21

国家自然科学基金项目(U1361118);湖南省自然科学基金项目(2015JJ2061);湖南省教育厅资助项目(14C0425)

章晓伟(1990-),男,江西省上饶人,硕士,研究方向:矿井通风与安全,E-mail:604801006@qq.com。

王海桥(1962-)，男，湖北省武汉人，教授，博士，研究方向：工业通风及空气洁净技术，E-mail：hqwang1962@126.com。

10.3969/j.issn.2095-7262.2015.05.005

TD724; O357.3

2095-7262(2015)05-0489-04

A