基于径向基网络模型的机床主轴箱咖误差模型研究

牟 菊，马术文

（1.中航工业成都飞机工业（集团）有限责任公司，成都 610091；2.西南交通大学机械工程学院，成都 610031）

基于径向基网络模型的机床主轴箱咖误差模型研究

牟 菊1，马术文2

（1.中航工业成都飞机工业（集团）有限责任公司，成都 610091；2.西南交通大学机械工程学院，成都 610031）

由于机床主轴转速相对机床其它运动部件的运动速度较高，所以机床主轴热误差在机床热误差中占有很大的比例，严重影响数控机床的加工精度。机床热误差建模在热误差补偿过程中具有非常重要的意义，文章针对某立式三轴加工中心的主轴箱，利用径向基神经网络模型理论，研究机床主轴箱关键测温点温升和机床热误差之间的关系模型。通过和线性回归模型对比分析，表明径向基神经模型能有效地提高热误差模型的精度。

径向基神经网络；主轴热误差；热误差模型

0 引言

数控机床运行过程中的热误差占机床总误差的75%［1］，在精密加工中甚至达到80%。在机床热误差中，由于主轴转速相对其它运动部件的速度更高，所以主轴轴承摩擦发热引起的热误差是机床热误差的主要组成部分。

为了有效进行机床热误差补偿，必须建立正确的机床热误差模型。最常用的机床热误差模型是利用统计理论，建立测温点温升和热误差的多元线性回归模型［2-3］。多元线性回归模型简单，在热误差补偿实现方面相对比较容易，但机床上各个测温点的温升和热误差之间不是简单的线性关系，限制了多元线性回归模型的精度。Dong Soo Lee应用机床主要热源相关的测温点温升作为热误差输入，建立基于热误差和测温点温升的多元二次回归模型，据报道在实际机床上补偿结果表明可以将Z向热误差从155.5μm降低到3.5μm［4］。张奕群等在对数控机床热特性分析的基础上，认为主轴轴承摩擦生热是最大的内热源，对热误差起主要作用，主轴轴承的摩擦热与主轴转速有直接的关系，因此建立基于主轴转速及的热误差线性差分方程模型［5］。张国雄和Yiding Wang利用灰色系统理论建立热变形误差的线性微分方程，通过求解微分方程建立热误差模型，证明可以补偿70%的热误差［6］。由于人工神经网络系统可以通过学习的方法来不断地修正模型以逼近实际系统，所以可以逼近任意非线性系统，并在机床热误差建模中也得到了较为广泛的应用。Narayan Srinivasa和Christopher D应用模糊ARTMAP（Adaptive Resonance Theory Modules Map）神经网络算法通过两次热工作循环的训练学习来预测机床的动态热误差［7-10］。

由于径向基人工神经网络系统结构简单，从而可以降低模型计算热误差的时间，提高误差补偿的实时性，所以本文针对某型号的立式加工中心的主轴箱部件，应用径向基神经网络模型对机床主轴的热误差模型进行研究。

1 研究对象及测温点的选择

本文以如图1所示的立式加工中心的主轴箱为研究对象，其主轴箱的结构如图2所示。虽然采用了油冷装置对该机床主轴部件进行冷却，但在运行过程中由于主轴轴承的摩擦，仍然在主轴部件上产生了较大的温升，破坏了机床的加工精度。机床运行结果表明，当主轴转速达到3000r/min时，机床在Z方向上存在较大的热误差达到109μm，Y方向的误差最大值为34μm，在X方向上由于左右对称，热误差量较小，没有必要进行补偿。

径向基人工神经网络热误差模型的输入为加工中心主轴箱上测温点的温升。如果输入变量增多，在使数据采集系统和神经网络模型的结构复杂化，增加运算的时间，降低补偿的实时性。通过初步试验，首先在机床主轴箱上选择了8个温升比较明显的测温点，通过模糊聚类算法把这八个测温点进行优化，最终选择测温点1和3的温升作为热误差模型的输入。

图1 立式加工中心结构图

图2 机床主轴测温点分布示意图

2 热误差补偿的神经网络模型研究

2.1 热误差神经网络模型结构

通过对径向基神经网络的分析，并结合对机床主轴箱的具体分析，建立热误差补偿的径向基人工神经模型如图3所示。

第一层为径向基层，其径向基函数选用高斯函数，表达式如下式：

式中ti为基函数的中心，σi高斯函数的方差，ΔT为测温点的温升向量。

第二层是线性层，选用线性传递函数，如Z向误差的传递函数可用下式表示：

式中：a1，a2，…，aq为隐层的输出值，线性层的输入值；w2z1，a2z2，…，a2zq为线性层的权值；bz为阈值。

图3 热误差径向基神经网络模型

2.2 热误差神经网络模型隐层节点数的确定

在应用径向基神经网络求解热误差模型时，需要确定隐层神经元的个数。如果隐层神经元数目太少，网络不具备必要的学习能力和信息处理能力，无法准确建立热误差模型；如果隐层神经元数目过多，在增加网络结构的复杂性和计算时间的同时，会使网络的泛化能力下降。对非训练的样本产生非期望的错误结果。本文参考文献［11］应用模糊聚类方法确定隐层的神经元数目。

（1）根据训练样本数据建立新型的数据样本集

训练样本集中的数据由测温点温升和Y、Z向热误差的实验数据组成，输入部分为（ΔTi，k），输出为（ΔYi，l）（i=1，2，…，n，为样本数目，k=1表示测温点1的温升，k=3表示测温点3的温升，l=1表示Y向热误差，l=2表示Z向热误差）。

把输入温升数据和输出热误差数据映射成一个n行4列的数据矩阵，前两列依次为测温点温升，后两列为Y向和Z向热误差值：

（2）对数据样本规格化处理

对矩阵（3）的数据应用均值处理的方法进行规格化处理，得到如下矩阵：

其中

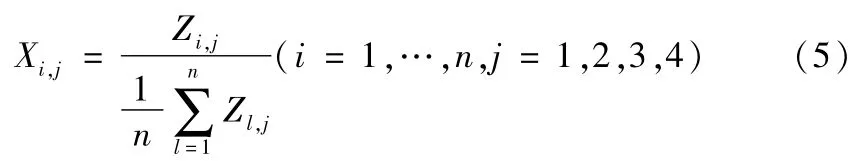
（3）计算相似性程度

计算相似程度的方法很多，选用相似系数法度量任意两个训练样本之间的相似性，即

（4）构造相似矩阵并确定样本分类数

根据相关系数可以确定出相似矩阵R=（rij）n×n，根据相似矩阵，取P个阈值λi（i=1，2，…，n），λi为R中第i行中除对角线上的元素外的最大元数。然后对λi排序，根据λi发生显著变化的次数加1作为隐层神经元的个数。

2.3 热误差神经网络模型的参数的确定

在建立热误差径向基神经网络模型过程中需要确定基函数的中心、高斯函数的方差和线性层的权值和阈值。这些参数的选取实际上就是神经网络的训练过程。

（1）中心点的确定

在应用模糊聚类原理对训练样本分类之后，基函数的中心点可以取为第i类训练样本的温升点的均值，即

NL为属于ZL的样本的数目。

（2）方差的确定

高斯函数的方差σi可以取第i类训练样本的均方差，即：

（3）权值和阈值的确定

在确定了中心点和方差后可以根据训练样本的输入向量和输出向量，利用最小二乘法计算线性层的线性传输函数的权值和阈值。

2.4 热误差与温升之间的神经网络关系模型

根据径向基神经网络的结构图和参数，可以建立热误差神经网络的关系模型，如Z向热误差关系模型：

3 人工神经网络模型在加工中心的仿真结果分析

为了识别径向基神经网络模型的参数，在机床冷启动的情况下，让主轴分别以1500r/min和3000r/min的转速运行，测量测温点的温度和主轴在Y和Z方向的热误差。在测量Y方向热误差时，在主轴上安装一刀杆，分别测量刀杆上端和下端的热误差，其数据如表1所示。把表1的实验数据作为训练样本，通过模糊聚类分析，所有样本按水平值排序，以水平值λ变化超过0.001作为显著变化，可以把41个样本分为7组，如表2所示。

表1 试验测量的样本数据

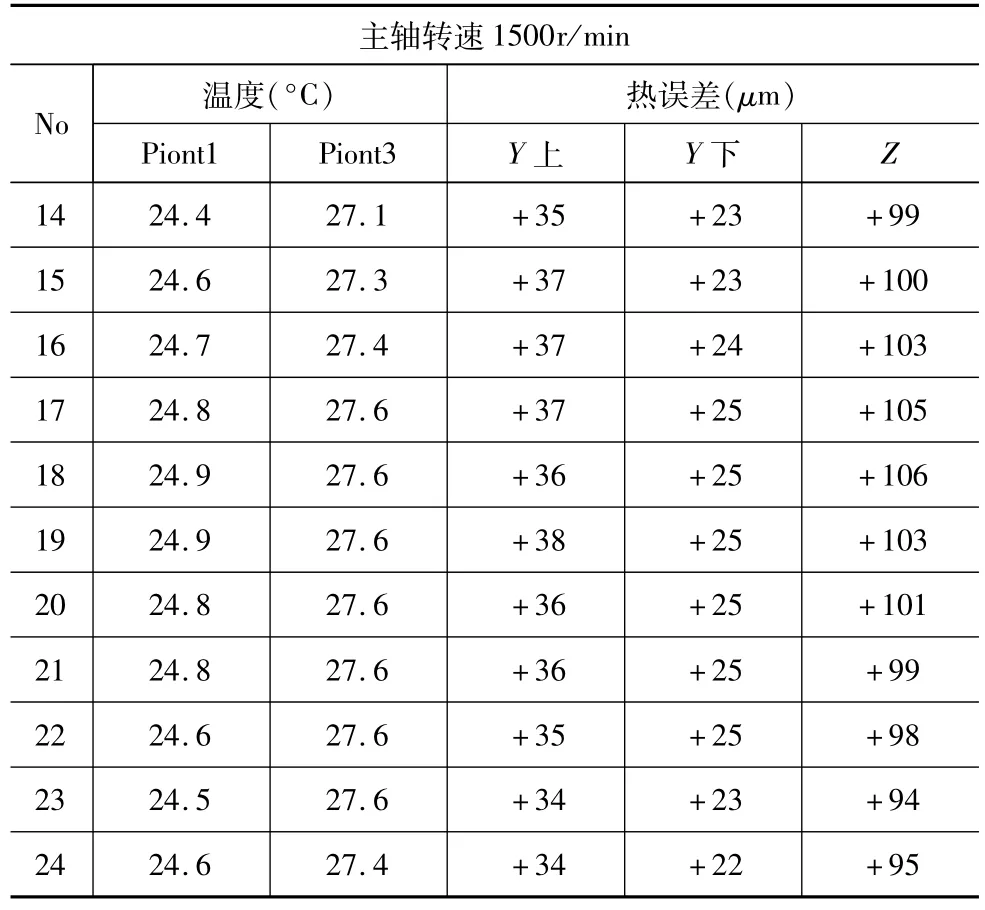
续表

表2 训练样本的模糊聚类后水平值λ排序

根据表2的训练样本分类结果，对每一类计算中心点和方差，可得表3的结果。

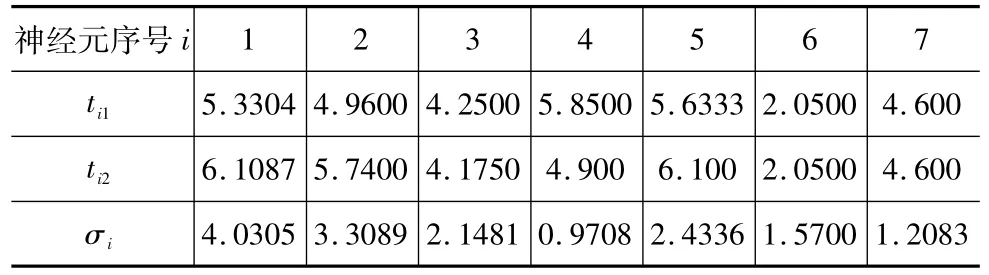
表3 径向基函数的中心和方差

根据训练样本值及中心点、方差，利用线性回归算法计算得到线性传输函数的权值和阈值如表4所示。

表4 线性层传递函数的权值和阈值

把表1的测温点数据，以测温点1和测温点3的温升作为径向基神经网络的Z向热误差模型的输入向量，计算热误差补偿量，，与真实测量值比较，计算其残差为 406.1，应用线性回归模型计算的残差为469.4。说明人工神经网络模型可以更精确地逼近真实的热误差模型，提高热误差补偿精度，降低热误差。

4 结束语

本文针对某型号三坐标立式加工中心的主轴，研究了径向基神经网络在主轴热误差建模中的应用。首先，确定了测温点温升和热误差的径向基神经网络模型的总体结构；其次，利用模糊聚类分析理论对训练样本进行了分类，根据分类结果确定径向基隐层神经元的数目及径向基函数的参数，并在此基础上利用回归分析的最小二乘算法来确定了线性层的权值和阈值；最后根据对某加工中心主轴箱上的温升和热误差数据进行数据分析，并将分析结果和线性回归分析结果进行比较，说明径向基神经网络模型能够更好地逼近实际的热误差模型，从而降低热误差。

［1］SR Postlethwaite，J P Allen，D G Ford.Machine tool thermal error reduction—an appraisal［J］.Proc Instn Mech Engrs.1999，213：1-10.

［2］Jianguo Yang，Jingxia Yuan，Jun Ni，Thermal error mode analysis and robust modeling for error compensation on a CNC turning center［J］.International Journal of Machine tool& Manufacture，1999，39：1367-1381.

［2］马术文，徐中行，刘立新，等，XH718加工中心的热误差补偿研究［J］.机械科学与技术，2007，26（4）：511-514.

［4］D SLee，JY Choi，DH Choi.ICA based thermal source extraction and thermal distortion compensation method for a machine tool［J］.International Journal of Machine Tools& Manufacture，2003，43：589-597.

［5］Shuhe Li，Yiqun Zhang，Guoxiong Zhang.A Study of Pre-Compensation for Thermal Errors of NC Machine Tools［J］.International Journal of Machine Tools&Manufacture，1997，37：1715-1719.

［6］Yiding Wang，Guoxiong Zhang，Kee SMoon，et al.Compensation for the thermal error of amulti-axis machining center［J］.Journal of Materials Processing Technology，1998，75：45-53.

［7］Narayan Srinivasa，John C Ziegert.An Application of Fuzzy ARTMAP Neural Network to Real-time Learning and Prediction of Time-Variant Machine Tool Error Maps［C］.IEEE，1994：1725-1730.

［8］Narayan Srinivasa，Jhon C Ziegert.Automated measurement and compensation of thermally induced error maps in machine tools［J］.Precision Engineering，1996，19：112-132.

［9］Christopher D Mize.Evaluation of Thermal Models on a machining Center［D］.the Degree of Doctor of Philosophy in U-niversity of Florida，1998.

［10］Christopher D Mize，John C Ziegert.Neural network thermal error compensation of a machining center［J］.Journal of International Societies for Precision Engineering and Nanotechnology，2000，24：338-346.

［11］吴成茂，范九伦.确定RBF神经网络隐层节点数的最大矩阵元法［J］.计算机工程与应用，2004（20）：77-79.

（编辑 赵蓉）

Research on the Thermal Error Model of Spindle Based on Radial Base Function Neural Network

MOU Ju1，MA Shu-wen2
（1.AVIC Chengdu Aircraft Ind.（Group）Ltd.，Chengdu 610091，China；2.School of Mechanical Engineering，Southwest Jiaotong University，Chengdu 610031，China）

For the spindle revolves in higher speed than other motion parts，the thermal error of spindle is the most major proportion of the thermal error of a NC machine tool.The machining accuracy will be reduced severely.So modeling and compensating thermal error are very important works in precision machining.In this paper，the relation model between thermal error and temperature rise on temperature measuring points has been researched through radial base function（RBF）neural networks in a spindle box of a 3 axis vertical center.RBF neural network can improve the accuracy of thermal error than multiple regression through simulation analysis.

radial base function neural network；thermal error of spindle；thermal error model

TH166；TG65

A

1001-2265（2015）06-0083-04 DOI：10.13462/j.cnki.mmtamt.2015.06.023

2015-01-28；

2015-03-26

牟菊（1980—），女，四川乐山人，中航工业成都飞机工业（集团）有限责任公司工程师，从事飞机制造工艺设计工作；通讯作者：马术文（1968—），男，四川眉山人，西南交通大学副教授，工学博士，研究方向为数控机床加工精度，（E-mail）mashuwen@home.swjtu.edu.cn。