基于IMF熵的多传感器网络融合滚动轴承故障诊断方法研究*

任学平，辛向志，庞 震，邢义通，王建国

（内蒙古科技大学机械工程学院，内蒙古包头 014010）

基于IMF熵的多传感器网络融合滚动轴承故障诊断方法研究*

任学平，辛向志，庞 震，邢义通，王建国

（内蒙古科技大学机械工程学院，内蒙古包头 014010）

经验模态分解（Empirical Mode Decomposition，EMD）方法可使滚动轴承振动信号根据自身尺度自适应的分解为若干个固有模态分量（Intrinsic Mode Function，IMF），信息熵能反映系统的不确定程度，滚动轴承发生故障会导致信息熵发生变化，结合EMD与信息熵，提出了EMD空间状态特征谱熵和IMF奇异谱熵，将其作为概率神经网络的特征向量，构建多传感器系统的多个概率神经网络的初级诊断网络。由于概率神经网络累加层输出结果为属于每一种模式的概率值，用概率神经网络的累加层输出结果构建D-S证据理论的mass函数，通过D-S证据理论进行决策级融合诊断。将该方法用于滚动轴承故障模式分类，试验结果表明该方法的可行性与有效性。与单一传感器诊断相比，提高了故障诊断精度。

多传感器；网络融合；滚动轴承

0 引言

滚动轴承故障诊断通常是通过加速度传感器采集其振动信号，而如何有效的分解信号并从中提取出有效识别故障的特征是滚动轴承故障诊断与识别的关链［1-2］。滚动轴承故障振动信号具有非平稳、非线性的特点，EMD（Empirical Mode Decomposition）方法是一种时频分析方法，能够将信号自适应的分解为若干个IMF（Intrinsic Mode Function），将非平稳信号转化为平稳信号［2］。

奇异值熵［3-5］可以评估信号的组成成分和分布特征，信号能量越集中，信号越确定，信号的奇异值熵越小。文献［4-5］提出了EMD奇异值熵，分别应用于转子系统的故障诊断和刀具磨损状态识别中。上述EMD奇异值熵的构造方法虽能区分不同故障，但区分度不大。针对此问题，本文通过构造EMD空间能量矩阵，对EMD奇异值熵进行改进，并命名为EMD状态空间特征谱熵，应用于滚动轴承故障诊断识别中，能非常好地区分不同类型的故障特征。EMD奇异值熵或是本文提出的EMD状态空间特征谱熵都是对信号总体特征的定量描述，并没有反映信号经EMD分解后的的局部信号特征，所以本文提出将主要IMF分量用来构造IMF奇异谱熵，来评估信号的局部特征。

概率神经网络（Probabilistic Neural Network，PNN）是神经网络的一种。与BP网络相比训练时间仅仅略大于读取数据时间；可以对复杂问题进行分类，并能得到贝叶斯准则下的最优解；需要增加或减少训练数据时，无需重新进行长时间训练；适用于小样本、非线性的模式识别［6-7］。D-S（Dempster-Shafer）证据理论是信息融合技术经典方法，但存在基本概率分配函数很难构建的问题，大多数都是采用不同的算法来构建。由于PNN累加层输出结果为属于各个类别的概率值，提出用其直接用来构建基本概率分配函数，从而解决了难于构建基本概率分配函数的问题。

将上述优点结合，本文从奇异值熵与EMD方法的角度出发，将滚动轴承振动信号先进行EMD分解得到若干个IMF分量，然后构造时频域的EMD空间状态特征谱熵和IMF奇异谱熵，并将其作为多传感器PNN的特征向量，通过各个单一PNN进行初步诊断，然后由D-S证据理论进行决策层融合诊断，取得了令人满意的效果。

1 基本理论

1.1 EMD方法

EMD方法可以把非平稳信号分解成一系列不同时间尺寸特征的IMF分量和残余分量之和。每一个IMF分量要达到2个条件［8］：①每一IMF其极值点个数与过零点个数要相等或者最多相差一个，②其局部极值上下包络线的的平均值要为零。

设原始信号为x（t），EMD方法的具体步骤是［8］：

（1）确定信号中所有的局部极大值点和极小值点，然后用三次样条曲线分别拟合上、下包络线，用m1代表上、下包络线的平均值，得出

求出的h1如果满足IMF条件，则h1就是x（t）的第1个IMF分量。

（2）若h1不满足IMF条件，就把h1作为原始数据，重复执行步骤（1），可以求出上下包络线的平均值m11，再判断h11=h1-m11是否满足IMF的条件，如其不满足，则重新循环（1）直到产生满足第1个分量条件的IMF。

（3）将c1从信号x（t）中分离出来，则

以r1作为原始数据，重复进行步骤（1）～（3）而最终得到信号x（t）的n个IMF分量和一残余分量rn，即

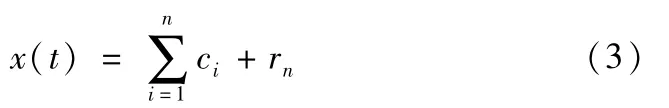
由式（3）可知，x（t）经EMD分解得到了n个IMF分量和一个残余分量rn之和，固有模态分量c1，c2，…，cn分别代表信号从从高频到低频的不同频段成分，残余分量rn代表信号的平均趋势。

1.2 EMD空间状态特征谱熵和IMF奇异谱熵

1.2.1 Shannon信息熵

信息熵可以定量评价系统的不确定性，反映系统的复杂度，刻画系统的自身成分。而滚动轴承工作过程中存在不同的故障时，其振动信号的确定性程度不同，所以信息熵值可以定量的反映滚动轴承运行中的振动信号的不确定性程度。

香农（Shannon）在自信息理论的基础上，将自信息中的数学期望定义为信息熵，表示为信息源的平均信息量：

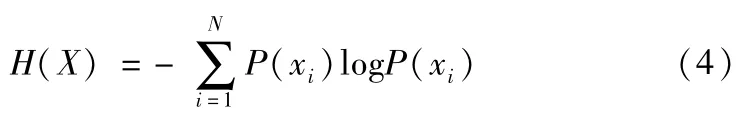
式中，设X=｛xi，i=1，2，3，…q｝为有q个状态的信源，P=｛Pi，i=1，2，3，…q｝为各状态出现的概率。

1.2.2 EMD空间状态特征谱熵

EMD奇异值熵虽能提取故障特征［4］，但却分度不大，故对其进行改进，定义为EMD空间状态特征谱熵。构建方法如下：

对于离散信号｛xt｝进行EMD分解，得到n个IMF分量c1，c2，…，cn和一个残余分量rn。EMD是将一维时域信号按从高频到低频自适应地映射到EMD空间上，EMD奇异值熵采用初始特征向量矩阵A=［c1c2…cn］T构建，并不能完全体现能量特征。因此，可定义由IMF分量和残余分量构成的EMD空间能量矩阵S，如下：

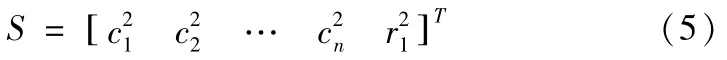
则S是对信号在时频域的一种划分，对S进行奇异值分解，则可以定义时频域的EMD空间状态特征谱熵为

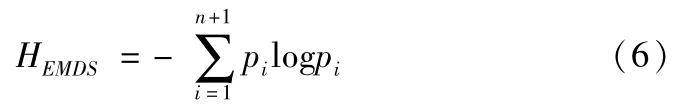
按上述方法计算正常、具有滚动体故障、具有内圈故障和具有外圈故障的滚动轴承振动信号的EMD空间状态特征谱熵，并按文献［4］的方法计算，结果如表1所示。

表1 不同工作状态滚动轴承的EMD熵

表中结果表明正常轴承的EMD熵值要大于故障状态时熵值，这是因为滚动轴承在正常状态下，其振动信号相对较小且平稳，能量分布相对平均和不确定。当出现故障（滚动体故障、内圈故障或外圈故障等）后，在相应的频带就会出现故障共振频率，此时，振动能量大部分集中在这个频带内，减小了能量分布的不确定性，从而使熵值减小。不同故障的共振频率不同，振动能量也不同，所以不同故障状态下的熵值也不同。所以，可以用该熵值识别不同故障状态。

同时，本文方法和文献［4］方法虽然都能区分不同故障，但本文方法区分度更大，识别效果更好；本文方法的熵值与文献［4］相比要小很多，由信息熵性质可知，本文方法降低了不确定性，可信度更高。

1.2.3 IMF奇异谱熵

对原始信号进行EMD分解得到的n个IMF分量c1，c2，…，cn，其中前几个IMF分量集中了信号中大多数的信息，称为主要IMF分量。利用延时嵌陷技术，分别对前几个IMF分量信号映射到嵌入空间，设空间的长度为M，则得到一个的N-M行M列的轨迹矩阵A，即

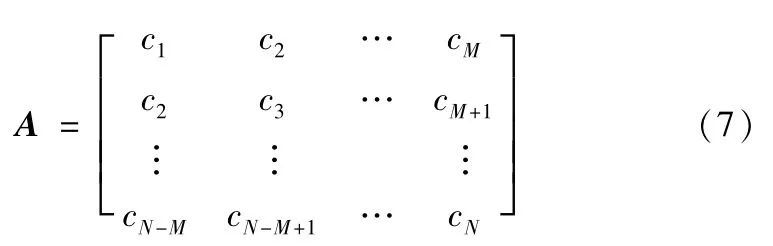
式中c为所选IMF分量值，本文中信号分解的IMF分量有7～10个，选前4个IMF分量重构。

对矩阵A进行奇异值分解，得到其奇异值δi，i= 1，2，…，M，则δi构成了IMF分量的奇异值谱。奇异值谱｛δi｝是对IMF分量的一种划分。所以我们可以定义IMF奇异谱熵为

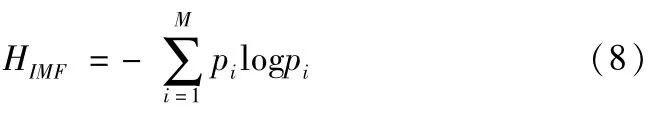
IMF奇异谱熵反映的是信号经过EMD分解后得到的平稳信号的复杂程度，滚动轴承发生不同的故障时，各个IMF分量不同，经相空间重构后奇异值分解会敏感地捕捉到信号的微弱变化，所以，IMF奇异谱熵可以敏感地反映滚动轴承的故障程度。

1.3 概率神经网络

PNN由Specht［6］提出，是以Parzen窗口函数为激活函数的一种前馈网络模型。融合了径向基神经网络与经典的概率密度估计原理的优点，常用于模式分类。图1为PNN网络结构图，PNN通常由输入层、模式层、累加层、输出层组成，各层主要功能如下。

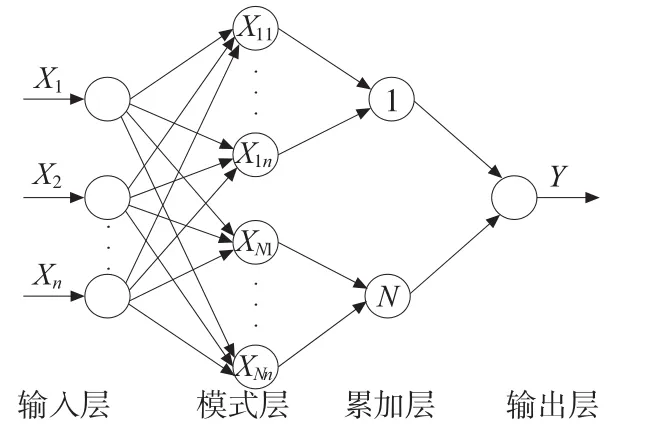
图1 PNN网络结构图

（1）输入层：这一层的作用只是将输入信号X用分布的方式表示，其传递函数是线性的，把同样的输入值提供给模式层的所有神经元。其中X=［x1，x2，…，xn］，n为输入单元总数。

（2）模式层：模式层与输入层之间通过权值ωij相连接，该层第j个神经元的实际输入为

这层的传递函数是

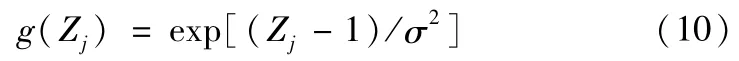
式中，σ为平滑参数。

（3）累加层：将属于每一模式的概率相加，计算每一模式的概率值。

（4）输出层：将累加层的结果通过竞争函数判别输出结果。

1.4 D-S证据理论

（1）基本概率分配

设Θ是一个样本空间，又称假设空间。在样本空间Θ上的BPA（Basic Probability Assignment基本概率分配，简称BPA）是一个2Θ→［0，1］的函数m，称为mass函数［9-10］。并且满足

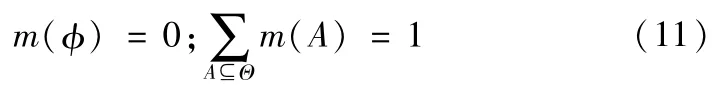
其中，满足m（A）＞0的A称为焦元。

信度函数Bel定义为

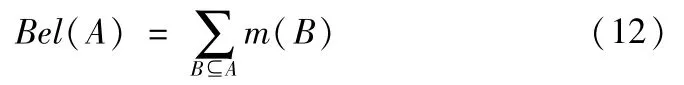
Bel（A）表示对A的信任度，也称为下限函数，表示命题成立的最小不确定性函数。

（2）证据组合原理

对于∀A⊆Θ，在样本空间Θ上的有限个mass函数如m1，m2，…，mn的Dempster合成规则为

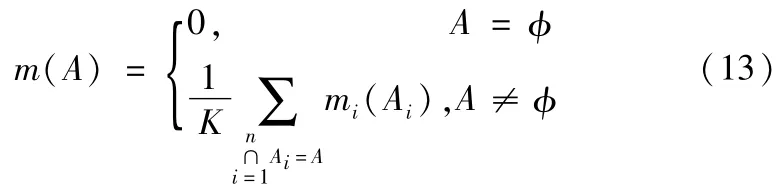
2 PNN与证据理论的融合故障诊断

基于PNN与D-S证据理论的融合滚动轴承故障诊断流程如图2所示，主要步骤如下：

（1）计算每一传感器振动信号的EMD空间状态特征谱熵和IMF奇异谱熵；

（2）分别由每个传感器的特征参数作为PNN的特征向量构建3个PNN初级诊断网络；

（3）3个PNN分别得出初级诊断结果；

（4）分别提取出3个PNN累加层输出结果，由DS证据理论将其进行融合，得出最终的决策级融合诊断结论。

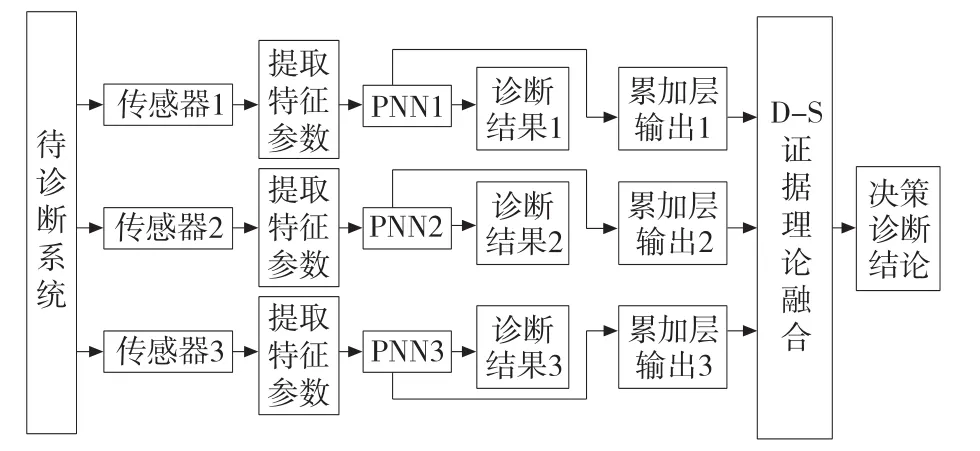
图2 PNN与D-S证据理论的融合故障诊断流程图

3 试验分析

本试验采用的试验设备是机械故障综合模拟试验台，由美国Spectra Quest公司生产制造，其主要研究的是基于振动响应的校准、平衡、共振和轴承故障等问题，试验台与传感器测点的位置如图3所示。试验的测试系统选用的是ZonicBook/618E型测试系统。

图3 实验平台

试验采用的故障轴承为MB ER-10K圆球滚子轴承，结构参数如表2所示。振动信号由安装在轴承座上的3个加速度传感器来采集，振动信号采样频率为2560Hz，分析频率为1000Hz，分析试验数据所使用的采样个数为2048个，采样时间为0.8s。

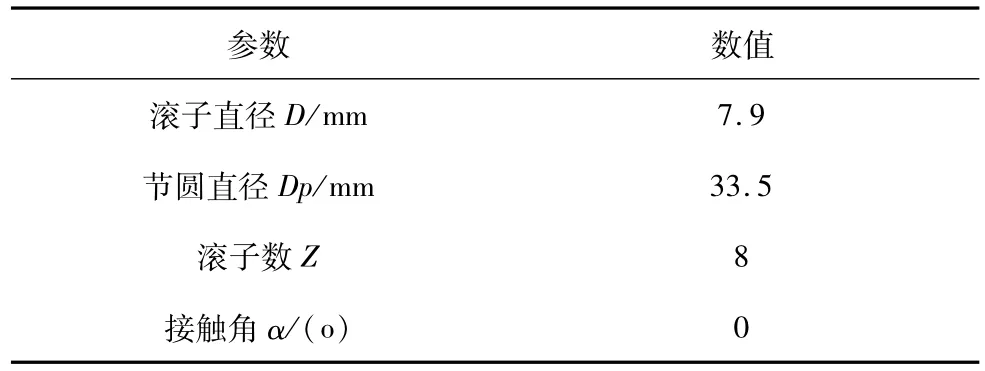
表2 轴承结构参数

试验用3个加速度传感器同步从3个不同方向测量试验轴承信号，转速为1260和1380r/min时分别测量10组，共对4种状态（正常状态、滚动体故障、内圈故障、外圈故障）轴承测得 80组数据。1260r/min时各传感器采集的4种状态轴承的信号如图4～图6所示。

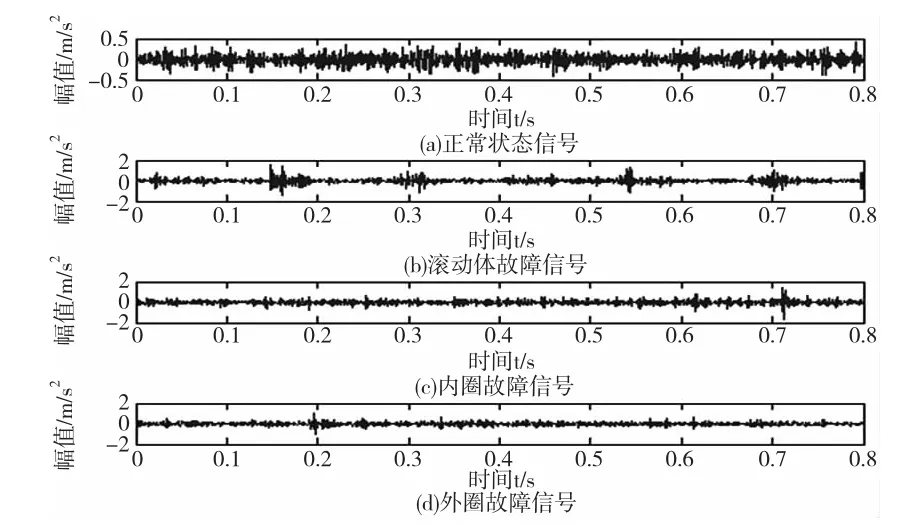
图4 传感器1滚动轴承信号时域振动波形

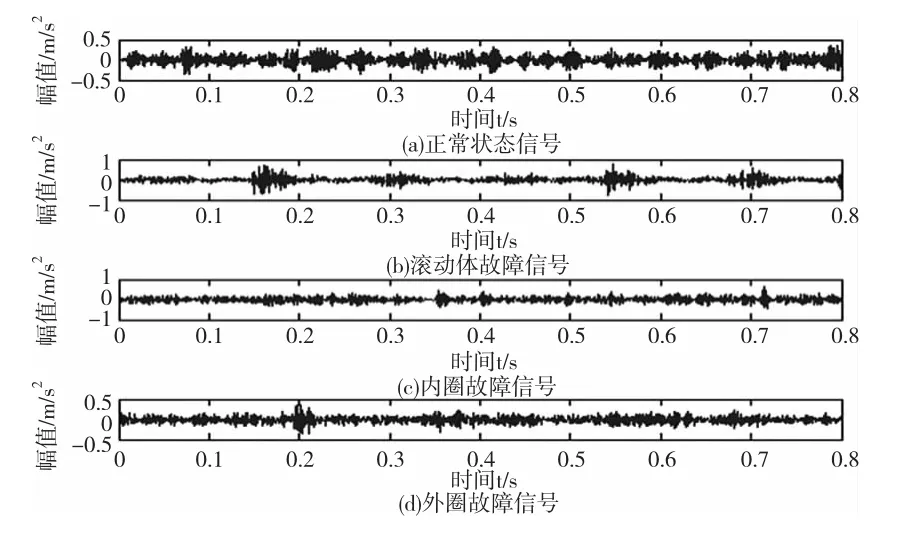
图5 传感器2滚动轴承信号时域波形

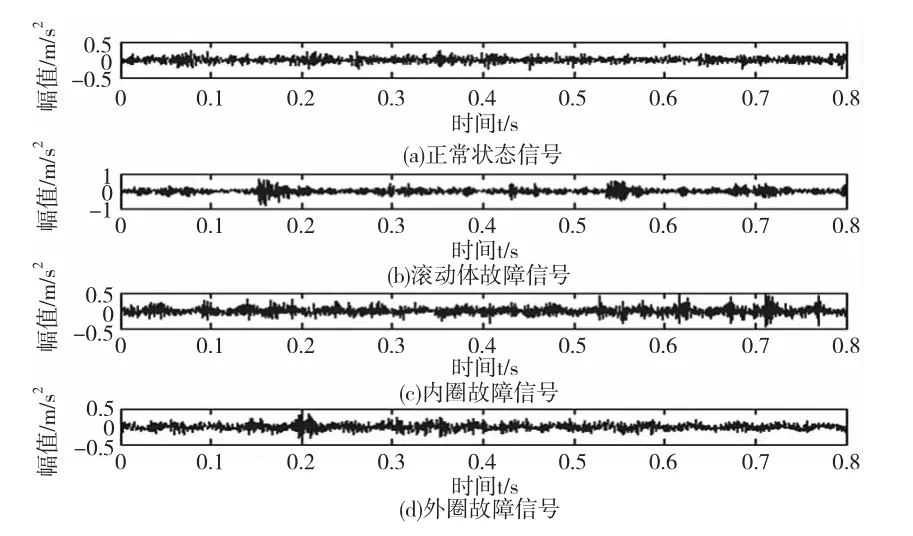
图6 传感器3滚动轴承信号时域波形

以第1个传感器采集的滚动体故障信号为例，EMD分解的前4个IMF分量信号如图7所示。可以看出前四个IMF已反映出主要振动特征。

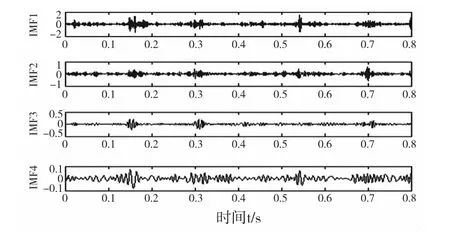
图7 滚动体故障轴承信号EMD分解结果

将1260r/min的数据作为PNN训练样本，1380 r/min的数据作为测试样本。首先分别从训练样本和测试样本中提取特征，分别计算EMD空间状态特征谱熵和IMF奇异谱熵，将所有数据进行归一化处理作为PNN的输入特征向量。表3为四种状态信号的部分特征向量。

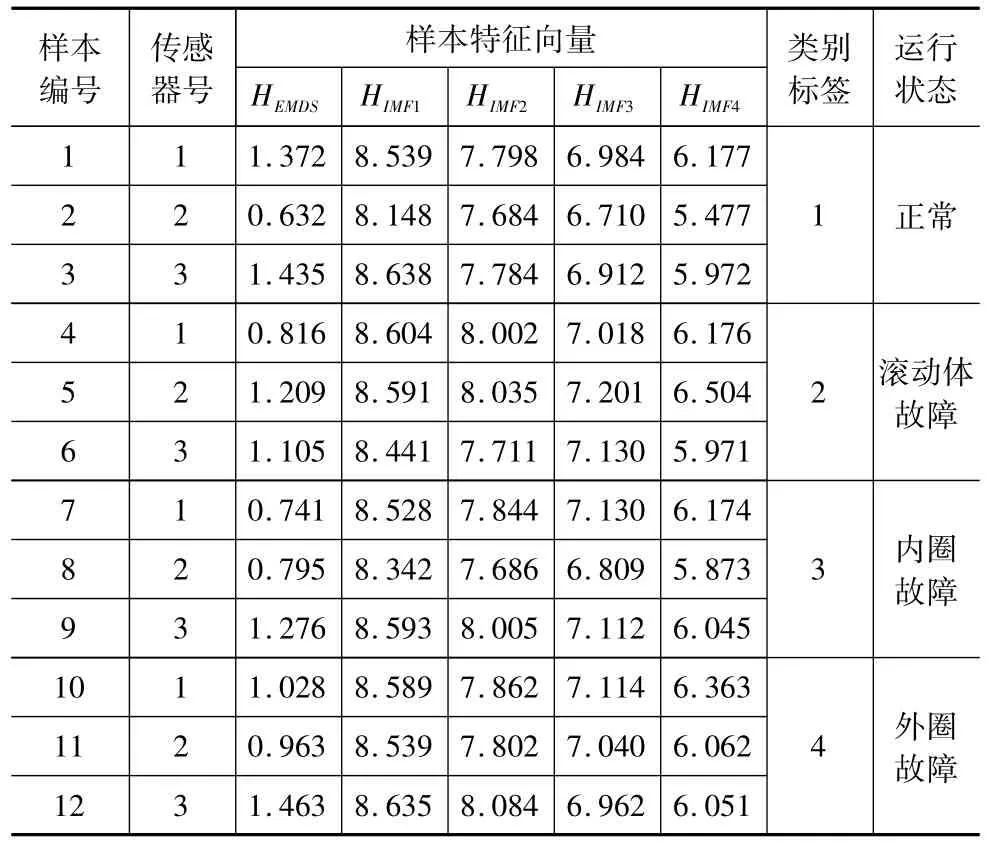
表3 部分特征向量样本

分别用传感器1、2、3的1260r/min的数据，将其归一化处理后训练PNN1、PNN2、PNN3，通过循环确定PNN1、PNN2、PNN3的最优平滑参数分别取σ1=0.2、σ2=0.1、σ3=0.1，然后分别用传感器1、2、3的1280r/min的数据测试训练好的PNN1、PNN2、PNN3，故障识别正确率如表4所示。

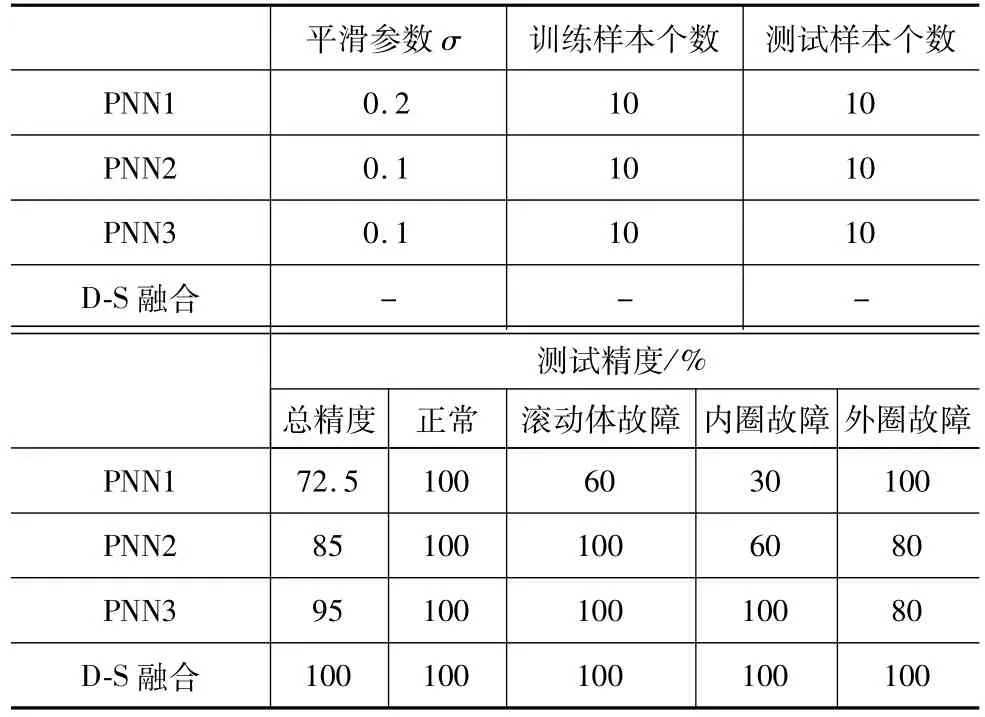
表4 PNN测试与D-S证据理论融合识别精度

通过表4中PNN初步诊断结果，分析比较可知，三个传感器对应的三个PNN的识别总精度以及对每一种状态的识别精度不等。传感器1对正常和外圈故障较敏感，PNN1对其识别精度达到100%，传感器2对正常和滚动体故障较敏感，PNN2对其识别精度达到100%，而传感器3对正常、滚动体故障和内圈故障较敏感，PNN3对其识别精度达到100%，但三个PNN中总识别精度最高95%，最低72.5%，差异较大，并且存在个别类别识别精度很低的问题，单一网络诊断效果不是很理想。

通常滚动轴承故障诊断信号是从x、y、z三个方向来获取，但没能通过计算给出综合的诊断结果。所以本文要通过构建融合模型来融合多传感器诊断系统，综合给出诊断结果，从而更加全面、综合地进行诊断。

由于PNN累加层输出结果为属于每一类的概率值，所以再将三个PNN累加层输出结果分别进行归一化求出属于每类的概率值，将其用作构建D-S证据理论的mass函数。将PNN1、PNN2和PNN3累加层输出通过D-S证据理论融合，融合后结果识别精度如表4所示，识别精度达到100%，达到了非常理想的效果。

4 结论

（1）改进了EMD奇异值熵，定义为EMD空间状态特征谱熵，改进前与改进后对滚动轴承不同的故障的识别结果表明：改进后的EMD奇异值熵相对于改进前对不同故障的区分度大幅度提升，效果明显；

（2）针对D-S证据理论的基本概率分配函数构建难的问题，提出将PNN累加层输出结果用来构建基本概率分配函数，从而简化了基本概率分配函数的构建过程，也使基本概率分配赋值符合了实际情况；

（3）将EMD空间状态特征谱熵和IMF奇异谱熵作为PNN特征向量，提出了多PNN—D-S证据理论的多传感器网络融合模型，试验验证表明该模型的有效性，提高了故障诊断的精度，对滚动轴承的故障诊断具有一定的指导意义。

［1］雷高伟，张清华，马春燕，等.基于信息融合的二重并发故障诊断方法［J］.组合机床与自动化加工技术，2014（5）：114-116，120.

［2］刘自然，熊伟，颜丙生，等.EMD方法和倒频谱在齿轮箱故障诊断中的应用［J］.组合机床与自动化加工技术，2014（9）：102-104.

［3］申弢，黄树红，韩守木，等.旋转机械振动信号的信息熵特征［J］.机械工程学报，2001，37（6）：94-98.

［4］于德介，陈淼峰，程军圣，等.基于EMD的奇异值熵在转子系统故障诊断中的应用［J］.振动与冲击，2006，25（2）：24-26，34.

［5］李庆，宋万清.IMF奇异值熵的刀具磨损状态诊断［J］.制造业自动化，2013（24）：52-55.

［6］Specht Donald F.Probabilistic neural netwoeks and polynomial Adaline as complementary techniques for classification.IEEE Transactions On Neural Networks，1990，1（1）：111-121.

［7］陈英俊，陈庆华.径向基函数神经网络在高速铣削表面粗糙度预测中的应用［J］.组合机床与自动化加工技术，2013（6）：6-8.

［8］王磊，张清华，马春燕，等.基于GA和EMD包络谱分析的滚动轴承故障诊断［J］.组合机床与自动化加工技术，2014（4）：53-56，59.

［9］叶汉民，肖尊定，宋子航.信息融合技术在异步电机故障诊断中的应用［J］.组合机床与自动化加工技术，2013（12）：86-89.

［10］秦海勤，徐可君，隋育松，等.基于系统信息融合的滚动轴承故障模式识别［J］.振动.测试与诊断，2011，31（3）：372-376，400.

（编辑 赵蓉）

Research of Rolling Bearing Fault Diagnosis Method Based on IMF Entropy and Multi-sensor Networks Fusion

REN Xue-ping，XIN Xiang-zhi，PANG Zhen，XING Yi-tong，WANG Jian-guo
（School of Mechanical Engineering，Inner Mongolia University of Science&Technology，Baotou Inner Mongolia 014010，China）

A rolling bearing vibration signal can be decomposed into a number of intrinsic mode function（IMF）adaptively according to its own scale with the empirical mode decomposition（EMD）method.The information entropy can reflect the uncertainty degree of the system.The rolling bearing failure w ill change the information entropy.EMD space state feature entropy and IMF singular spectrum entropy are proposed by combining EMD and information entropy.In the multi-sensor system，primary diagnosis network of multiple probabilistic neural networks was constructed and the feature vector of probabilistic neural network is EMD space state feature entropy and IMF singular spectrum entropy.Because output of accumulation layer of the probabilistic neural network are each kind of model of probability values，mass functions of D-S evidence theory can be built using these probability values.The fusion diagnosis of decision level proceeded by the D-S evidence theory.Using this method for rolling bearing fault pattern classification，the results of experiments show the feasibility and effectiveness of the method.Compared with the single sensor method in the diagnosis，it improved the accuracy of fault diagnosis.

multi-sensor；networks fusion；rolling bearing

TH16；TG506

A

1001-2265（2015）06-0078-05 DOI：10.13462/j.cnki.mmtamt.2015.06.022

2014-09-16；

2014-10-19

国家自然科学基金资助项目（21366017）；内蒙古自治区自然科学基金资助项目（2012MS0717）

任学平（1963—），男，河北阳原人，内蒙古科技大学教授，博士，研究方向为机械工程测试与故障诊断，（E-mail）rxp@imust.cn；通讯作者：辛向志（1989—），男，内蒙古赤峰人，内蒙古科技大学研究生，研究方向为机械故障诊断与信息融合技术研究，（E-mail）xinxiangzhi@126.com。