数控铣床进给伺服系统误差补偿的PID控制*

张 蕾，黄美发，林振广

（1.桂林电子科技大学机电工程学院，广西桂林 541004；2.桂林机床股份有限公司，广西桂林541001）

数控铣床进给伺服系统误差补偿的PID控制*

张 蕾1，黄美发1，林振广2

（1.桂林电子科技大学机电工程学院，广西桂林 541004；2.桂林机床股份有限公司，广西桂林541001）

进给伺服系统是数控机床的重要组成部分，但常规的PID控制器具有整定不良、性能欠佳和适应性差等缺点，不能满足实际加工的精度要求。对某型号数控铣床进给伺服系统常规PID控制器存在的问题进行分析，提出了加入全闭环控制和支持向量机PID控制系统的方法。通过补偿运动部件位移产生的误差，并将各传感器测量值反馈支持向量机PID控制系统，对PID控制参数进行自整定。通过仿真实验证实了该方法缩短了系统的调节时间，提高了系统抗干扰能力和适应力。

伺服进给系统；PID控制；支持向量机

0 引言

数控机床的伺服系统是实现机床进给运动、主轴运动及位置控制的关链的系统之一［1］。而进给伺服系统作为一个典型机电系统，涉及机械传动间隙、摩擦阻力、切削变形、负载惯量、温度变化、冲击振动、死区等非线性因素，成为提高伺服系统定位精度、跟踪精度及动态性能的瓶颈。这使得进给伺服系统难以建立精确的数学模型，而且传统的PID控制往往整定不良，性能欠佳，对机床运行工况的适应性很差。近10多年来，在常规PID控制基础上引入智能控制，形成所谓智能PID控制。这种新型控制器已引起人们的普遍关注和极大兴趣，并已得到较为广泛的应用［2］。

通过对企业某型号数控铣床的伺服系统的分析，该数控铣床采用半闭环控制，原有的编码器不能检测反映传动链上的间隙，传统PID控制的进给伺服系统不能解决实际加工过程中的非线性因素，对伺服系统的各项精度和动态性能有很大影响。针对上述问题，本文在前人理论研究的基础上，提出在运动部件上加入光栅尺传感器形成全闭环控制，反馈的位置和速度量输入支持向量机智能PID控制系统，实时补偿进给系统的位移误差，自动调节PID控制参数以优化时变和非线性的动态进给伺服系统，从而达到提高铣床加工精度的目的。

1 数控铣床误差补偿控制的实现

大多早期数控铣床的半闭环控制伺服电机上的编码器既作速度环，也作位置环，不能反映传动链上的各种间隙和误差。为了能获得更高的控制精度，在铣床工作台增加检测精度更高的光栅尺来测量运动机构位移量，以此实现数控铣床的误差补偿控制。

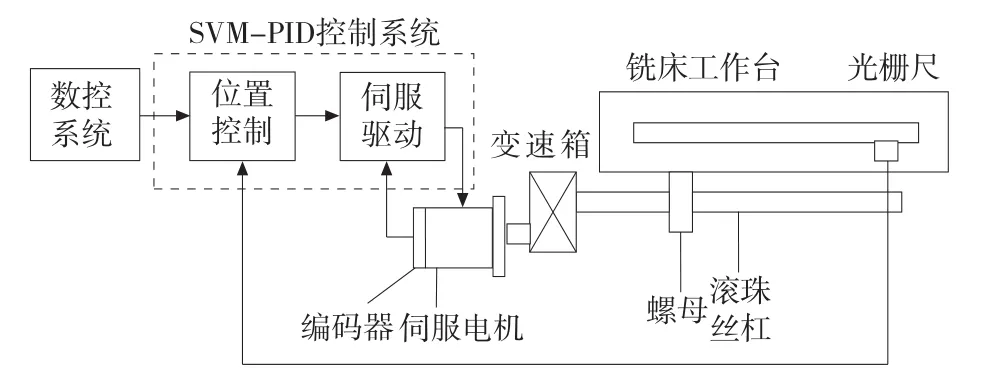
图1 数控铣床误差补偿控制系统组成

数控铣床进给伺服系统误差补偿控制工作原理如图1所示。伺服驱动控制伺服电机并通过编码器反馈速度量，从而实现数控车床的速度调节。光栅尺直接测量运动部件的实际位移量，减少机械系统因磨损、热膨胀、受力变形带来的位置误差，同时将其转换为电脉冲信号，并反馈到智能PID控制系统中，根据指令位置和实际位置之差，补偿运动部件的实际位移产生的误差，最后根据系统的输入、输出、位移和速度量，通过支持向量机实时优化PID的参数，减小加工过程中的非线性不确定性、时滞、随机扰动等产生的误差，并使伺服系统调节时间减少，响应速度加快，提高抗干扰和适应能力。

2 PID控制算法原理及其智能化改进

2.1 增量式PID控制算法

传统PID控制器采用增量式PID控制算法，其公式为：

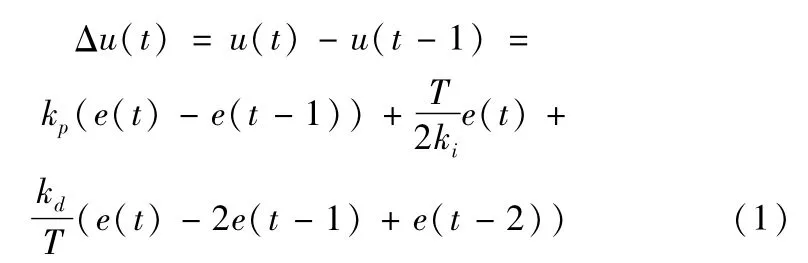
式中，kp、ki、kd分别为比例、微分、积分系数，e（k）为系统输入值与实际输出值的偏差，T为采样周期。重写上式：

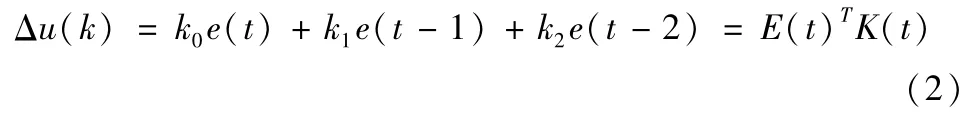
其中

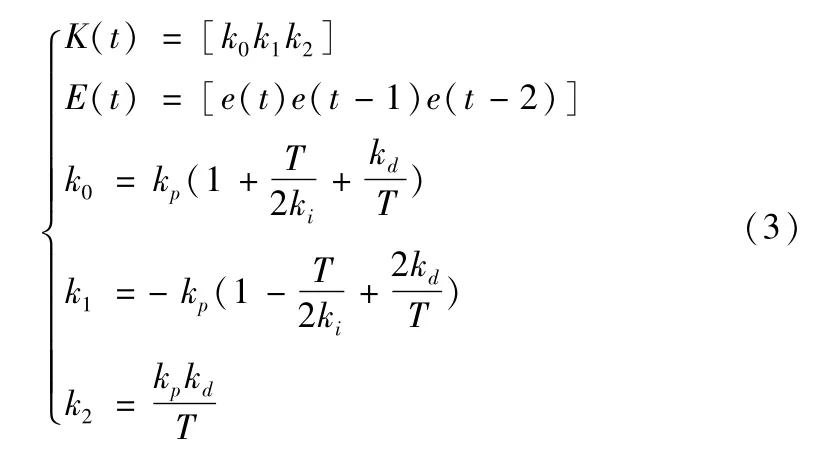
2.2 支持向量机PID参数自整定

为了解决传统PID控制无法满足数控铣床实际加工需要的问题，控制领域已经提出很多改进算法的PID控制器参数整定方法，其中，支持向量机PID控制是对常规PID控制的一种改进和优化。

支持向量机具有可靠的数理统计理论基础，可解决非线性的回归问题，通过SVM在线学习，可以得到数控铣床进给伺服系统PID控制的最优参数。基于SVM的PID控制系统结构如图2所示。

PID控制器通过编码器与光栅尺反馈的速度和位置量直接对进给伺服系统进行闭环控制，支持向量机回归系统根据伺服进给系统的速度与位置误差，调节PID控制器的参数，以使数控铣床实时加工效果达到最优。

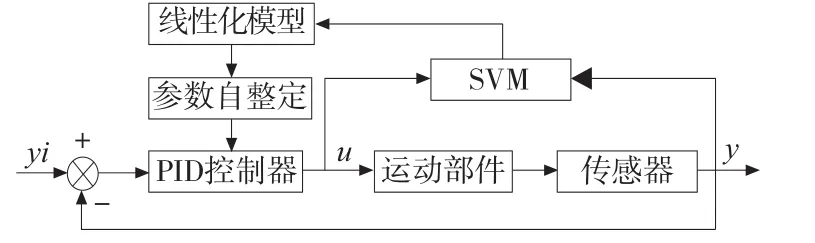
图2 支持向量机的PID控制系统结构

PID控制系统是让u（t）能够在（t+1）时刻使伺服系统的输出量与实际加工需要的输出量的差最小，因此目标函数可以这样构造：

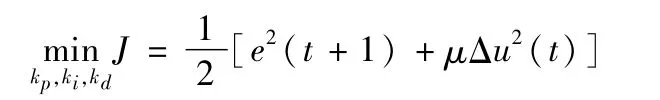
其中，e（t+1）=r（t+1）-y（t+1），上式右边第二项表示对控制信号的变化Δμ（t）的控制，u为惩罚系数。用瞬时线性模型来取代得：

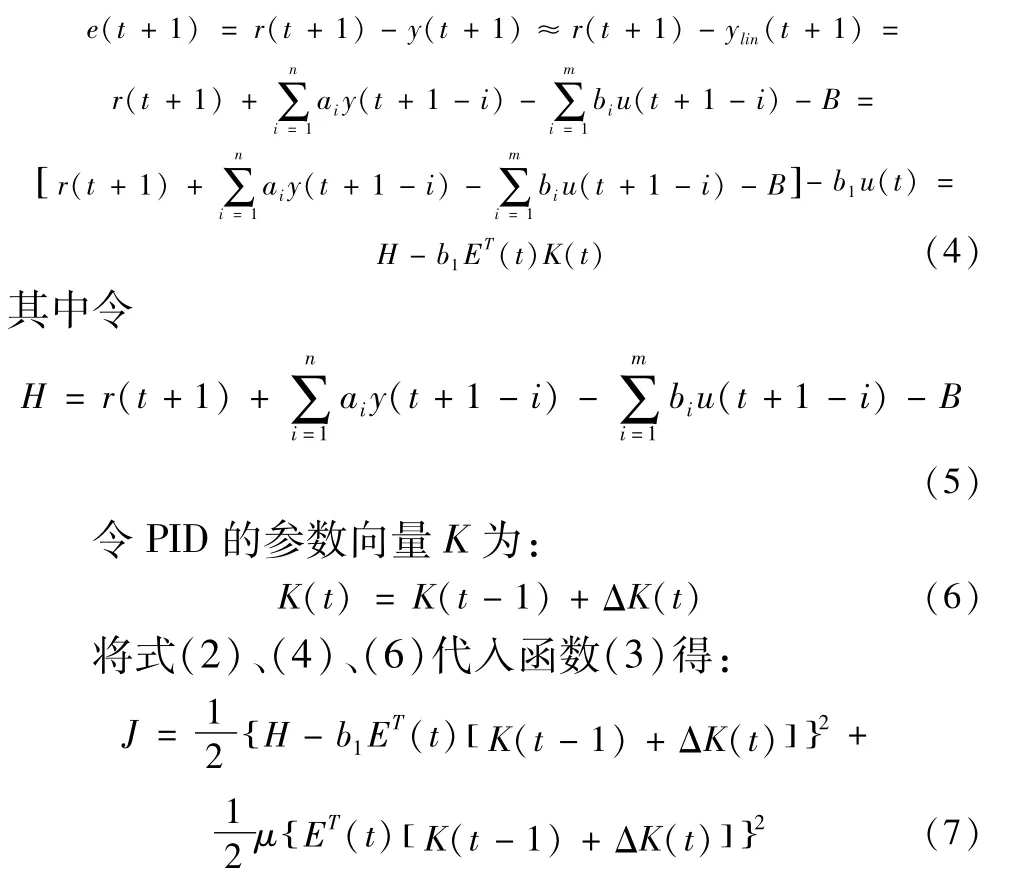
上式对ΔK求导并使之为0，可得J最小时ΔK的转化规则，即获得在最小化方差意义下最优的PID参数。

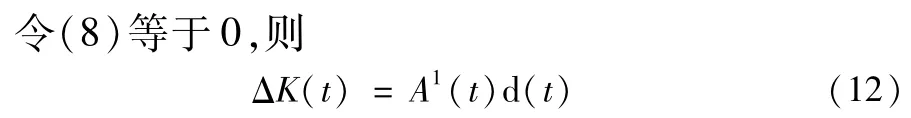
由式（12）、式（6）和式（3）可计算出PID控制器的参数为：

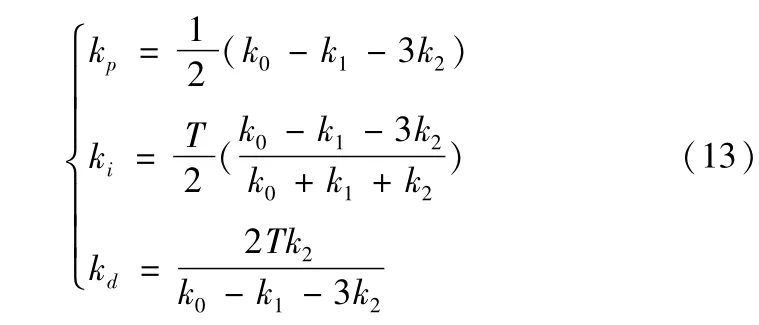
由（13）得到PID参数有可能出现负值，在实际应用中，要求PID参数为非负值，因此根据（13）可以确定PID参数的取值范围及约束条件如下：

这时目标函数仍然为（3）表示的二次函数，在上述线性不等式的约束下，利用二次规划的方法同样可以求取最优的PID控制器参数。

3 仿真实验

在磁场定向（id=0）控制方式下，数控铣床进给伺服系统的数学模型可以用以下传递函数来近似表示：

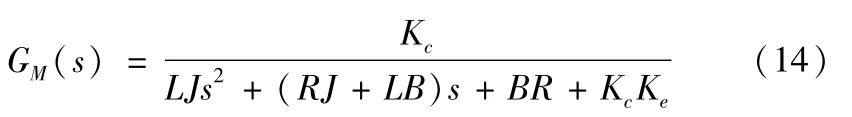
参考数控铣床资料，选定的仿真系数为电感L= 8.5×10-3（H），电阻R=2.857（Ω），总的转动惯量J=0.8×10-3（km·m2），总的粘性阻尼系数为B= 0.02（N·m（rad/s）），磁极pn=4，永磁磁通φf= 0.175（Wb），将上述参数代入式（14）得

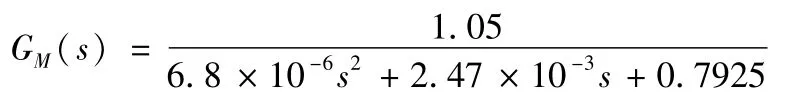
根据2.1中PID控制原理和2.2中所述控制器参数整定的步骤，得到数控铣床进给伺服系统支持向量机自整定PID控制与传统PID控制相比较的仿真结果如图3所示。

仿真结果表明，采用支持向量机自整定PID控制算法的数控铣床进给伺服系统与采用经典PID控制算法相比，系统调节时间减小，响应速度加快，抗干扰和适应能力都优于常规PID控制进给伺服系统。

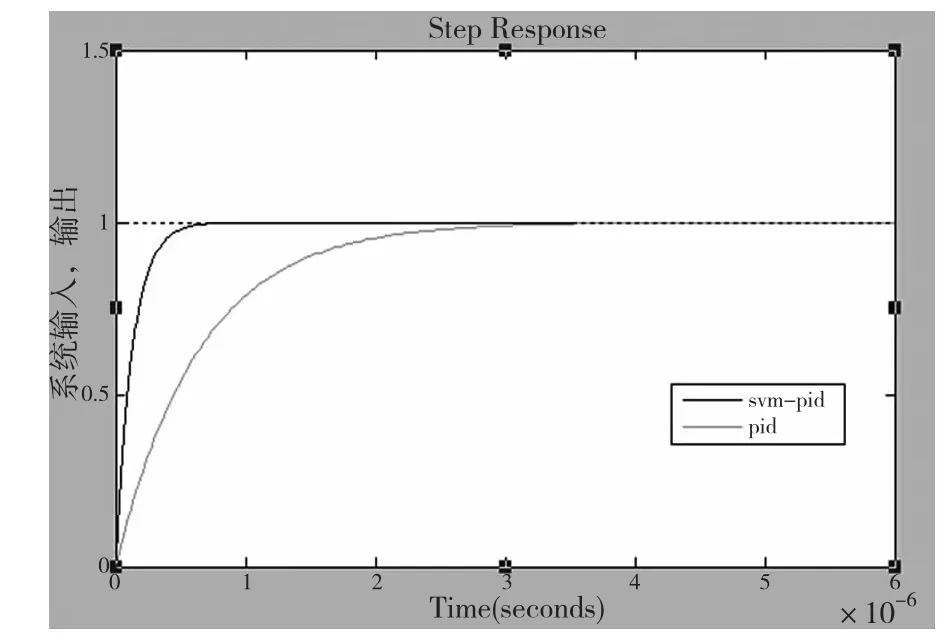
图3 系统阶跃响应曲线

4 结论

本文针对某型号数控铣床进给伺服系统上存在的问题，通过加入全闭环控制，减小了传动链上的间隙误差，并通过支持向量机PID控制系统，实时调节PID的参数使进给伺服系统达到最优，并通过仿真和对比实验来验证其有效性和优越性。

［1］王辉.CK6136数控车床交流伺服进给系统的分析与仿真［D］.浙江：浙江工业大学，2009.

［2］陶永华等编著.新型PID控制及其应用［M］.北京：机械工业出版社，1998.

［3］成文华.具有间隙非线性的伺服进给系统对轮廓加工误差的影响机理［J］.浙江大学学报：工学版，1999，33（6）：608-611.

［4］刘强，尔联洁，刘金现.摩擦非线性环节的特性、建模与控制补偿综述［J］.系统工程与电子技术，2002，24（11）：46-52.

［5］张学工.关于统计学习理论和支持向量机［J］.自动化学报，2000，26（1）：32-42.

［6］丁世飞，齐丙娟，谭红艳.支持向量机理论与算法研究综述［J］.电子科技大学学报，2011，40（1）：2-10.

［7］CHANGA W D，HWANGBR C，HSIEHA JG.A.self-tuning PID control for a class of nonlinear systems based on the Lyapunov approach［J］.Journal of Process Control，2002，12（2）：233-242.

［8］石文兵.数控机床进给伺服系统PID参数自整定仿真研究［D］.武汉：华中科技大学，2007.

［9］刘金琨.先进PID控制及其MATLAB仿真［M］.北京：电子工业出版社，2003.

［10］宋现春，林明星，艾兴，等.激光反馈螺纹磨床误差补偿系统的智能PID控制［J］.工具技术，2001，35（10）：13-15.

［11］左健民，王保升，汪木兰，等.超精密数控机床进给系统非线性分析及误差补偿研究进展［J］.南京工程学院学报（自然科学版），2007，5（1）：1-7.

（编辑 赵蓉）

CNC Milling Machine Feed Servo System Error Compensation of PID Control

ZHANG Lei1，HUANG Mei-fa1，LIN Zhen-guang2
（1.School of Mechanical and Electrical Engineering，Guilin University of Electronic Technology，Guilin Guangxi541004，China；2.Guilin Machine Tool Co.，Ltd.，Guilin Guangxi541001，China）

Feed servo system is an important part of cnc machine，and the conventional PID controller with setting bad，poor performance and adaptability，cannot satisfy the requirement of the actual processing precision.Analysis the problems of the existing conventional PID controller for a certain type of CNC milling machine feed servo system，put forward the method of adding the full closed loop control and support vector machine PID control system.By compensating the error of the displacement of the moving parts，and feedback the sensor measurements to support vector machine（SVM）PID control systems，self-tuning PID control parameters.Through the simulation experiments prove that the method can shorten the adjustment time of system，improve the system of anti-interference ability and adaptability.

feed servo system；PID controller；support vector machine

TH165；TG659

A

1001-2265（2015）06-0065-03 DOI：10.13462/j.cnki.mmtamt.2015.06.018

2014-09-14；

2014-10-11

国家自然科学基金（51365009）；广西制造系统与先进制造技术重点实验室主任课题（13-051-09-009Z）

张蕾（1987—），男，广西玉林人，桂林电子科技大学硕士研究生，研究方向为数控机床误差补偿，（E-mail）118052439@qq.com。