单面立式硬支撑动平衡测试机的设计研究

罗迪威，谢 轩，李 宾，曾 胜，顾超华

（浙江大学化工机械研究所浙大-集智研发中心，杭州 310027）

单面立式硬支撑动平衡测试机的设计研究

罗迪威，谢 轩，李 宾，曾 胜，顾超华

（浙江大学化工机械研究所浙大-集智研发中心，杭州 310027）

针对单面硬支撑动平衡测试机，进行了机器的动力学研究，分析了影响永久标定误差的因素，给出了板簧刚度、测力传感器安装刚度和预紧弹簧刚度的选取原则，制作了样机，进行实验测试以及最小可达剩余不平衡度测定。结果表明，按照设计方法设计的测试机具有较高的测试精度。

硬支撑；平衡测试机；刚度分配；永久标定

0 引言

按动力学特性，平衡测试机可分为硬支撑平衡测试机和软支撑平衡测试机。硬支撑平衡测试机的平衡测试转速远低于转子支撑系统的固有频率，从支撑测得的响应与转子的不平衡离心力成正比，所以它可直接反映出不平衡量，而毋需对具体转子进行针对性的标定工作。硬支撑平衡测试机适用于大中型转子的平衡测试。软支撑平衡测试机的平衡测试转速远高于转子支撑系统的固有频率，从支撑处测得的响应为振动位移信号，其振幅接近于转子的偏心。软支撑平衡测试机在测量之前需要对具体转子进行标定，且适用于小型转子的平衡测试。

现今关于两种支撑的平衡测试机的原理与结构形式已经非常成熟，市场上有各类丰富的产品可供选择。李顶根等［1］应用振动理论和最优化原理与方法，建立了摆架振动结构参数的优化数学模型，制出了具有静偶分离特性的新型式动平衡测试机的摆架结构。钟沈江等［2-3］以MCB-980通用硬支撑平衡机为基础，分离了各种测试方法的信号特点，建立了一种新的刚性转子的双面动平衡的数学模型，分析了求取动不平衡量大小和相位的原理，在此基础上开发了一种以工控机为主机的硬支撑动平衡测试机。但上述文献均未对平衡测试机的具体设计和实施案例进行详细解释。

课题组对包含平衡测试机的全自动平衡修正设备有多年研究［4-6］，探讨了软支撑平衡测试机的设计方法和实施案例，研发出了基于软支撑测试机的多工位全自动平衡修正设备，成功地应用到了批量生产的小型电机转子。对于大中型转子的平衡，由于需用硬支撑平衡测试机，故而本文将从机械结构的动力学出发，探索在使用压电传感器的情况下时，各参数对盘状立式硬支撑平衡测试精度的影响，通过实施案例及测试数据进行验证，为立式硬支撑全自动平衡修正设备的研发打下基础。

1 立式硬支撑平衡测试机结构

立式平衡测试机由主支承架、板簧、压板、振动体支座和旋转主轴组成，如图1a所示。旋转主轴固定在振动体支座上，两者构成振动体，振动体通过带有压板的两片板簧支承在刚性的主支承架上。测量时，被测转子工件通过夹具固定在振动体上。硬支撑平衡测试机振动系统的固有频率要比平衡转速高出数倍，因而采用较刚性的板簧。在支承架跟振动体支座之间，安装有仅能测量压力的压电陶瓷测力传感器。为了使传感器输出良好的不失真振动波形，可通过预紧弹簧，使其对传感器施加一定的预紧力。此时，板簧、传感器和预紧弹簧构成并联结构，平衡测试机总刚度是板簧刚度、传感器安装刚度和预紧弹簧刚度之和。这个总刚度决定了整个平衡测试机的固有频率。如何选择板簧刚度、预紧弹簧刚度、传感器安装刚度以及预紧弹簧的预压缩量，是硬支撑平衡测试机设计中比较重要的环节。

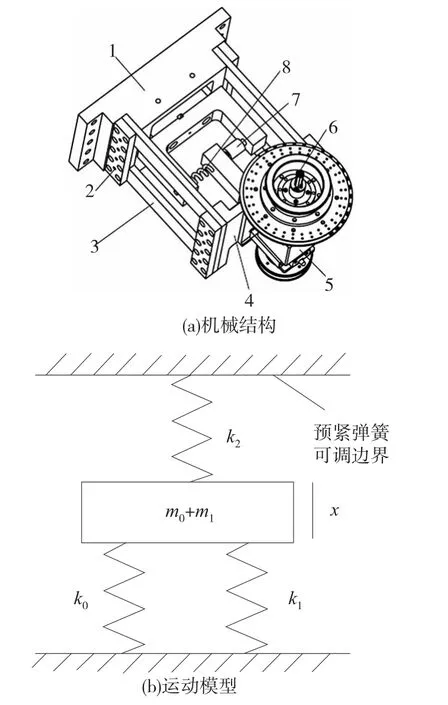
图1 平衡测试机支承结构

2 立式硬支撑平衡测试机动力学特性

2.1 运动方程

图1a中的平衡测试机可以简化为图1b所示的运动模型。其中振动体的质量为m0，被测转子工件的质量为m1，板簧的横向刚度为k0，传感器的安装刚度为k1，预紧弹簧的刚度为k2。当具有偏心e的被测转子工件以角速度ω旋转时，离心力m1eω2将使振动体发生振动，假设振动体在预紧弹簧预紧方向的位移为x，则振动体的运动方程为

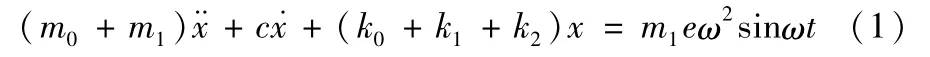
设M=m0+m1，K=k0+k1+k2，，ξ=，代入上式并求解，则可得到板簧、传感器和预紧弹簧受到的动态回复力之和Kx与离心力m1eω2幅值和相位差之间的关系

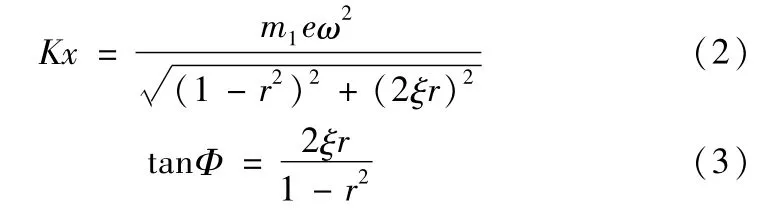
由于测力传感器仅承受部分回复力k1x，所以其输出为

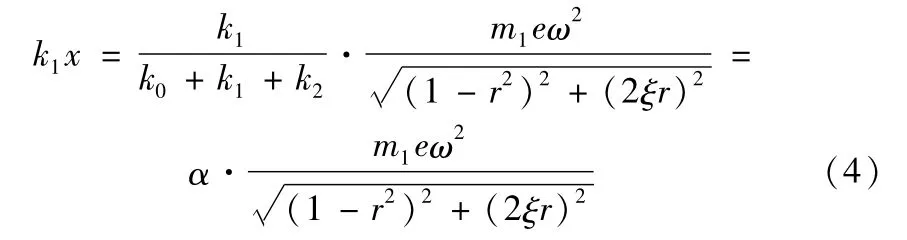
式（4）中，α=k1/（k0+k1+k2），为测力传感器安装刚度占总刚度的比例，或称刚度配比。

当k1x除以转速ω的平方后得到

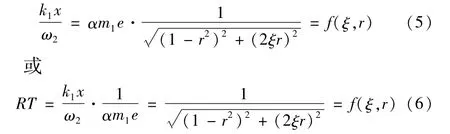
以频率比r为横坐标，阻尼比ξ为参变量，作出的RT=f（r，ξ）曲线，如图2所示。

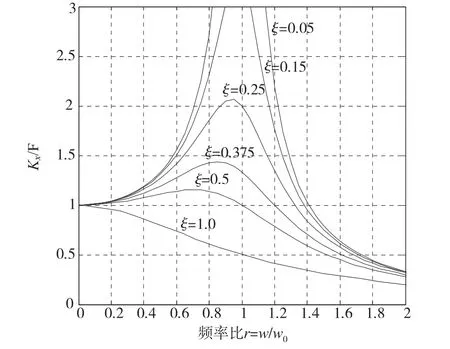
图2 RT=f（r，ξ）的响应曲线

2.2 硬支撑平衡测试机的永久标定

硬支撑平衡测试机推荐的频率比r≤0.3［7］，由于其没有特别的阻尼装置，故阻尼比ξ很小，ξ＜＜1。从图2可以看出，在频率比0＜r≤0.3和ξ≤0.5范围内：①当频率比r≤0.1时，RT趋近于1，且当阻尼比ξ=0时，RT与1的偏离达到最大值，偏差百分比约为1%；随着阻尼比ξ增大，偏差百分比逐渐减小；②当频率比0.1＜r≤0.3时，RT与1的偏离的值随频率比r增大而增大；特别地，当r=0.3且ξ=0时，两者差值最大，约达到10%。由于测力传感器的输出k1x仅和Kx相差常系数α，所以k1x与αωm1e之间也满足上述关系。

硬支撑平衡测试机具有永久标定的特点，其依据为：由于r≤0.3，故r2＜＜1，忽略r的影响（也就是忽略振动过程中惯性力的影响），式（6）中RT≈1，因故在某一转速ω下标定回复力k1x与不平衡量m1e之间的关系得到常系数α

在其他转速下，不管被测转子工件的质量m1的大小，都根据式（7）由常系数α、转速ω和回复力k1x计算不平衡量m1e。

根据上述分析，硬支撑平衡测试机在频率比0＜r≤ 0.3范围内，永久标定的最大误差约为10%；在频率比r≤0.1范围内，最大误差为1%。如果进一步减小频率比r，则最大误差继续减小。从这个意义上说，提高平衡测试机的固有频率，以降低频率比r，有利于降低测试误差。

当平衡测试机的振动体质量m0取得尽量小时，要提高其固有频率只能增加支撑刚度K。其中最有效的是增加板簧的横向刚度k0。但是这样做会使系数α减小，降低振动信号的灵敏度，所以需要根据支撑刚度K的组成，进行各分量的刚度分配。

2.3 硬支撑平衡测试机刚度分配

硬支撑平衡测试机的测力传感器一般采用压电材料作为敏感元件，其结构决定了传感器只能测量压力而不能测量拉力。被测转子产生的不平衡离心力m1eω2是一个周期力，因而需对测力传感器进行预紧，使测量得到的振动力信号有一正向偏置。为了使信号不失真，进行预紧的预紧力F预紧应大于最大不平衡力给予传感器的分量，即

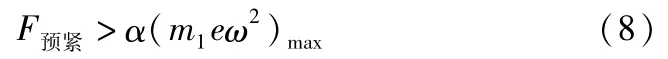
假定平衡测试机安装完毕后，预紧弹簧的预紧量为Δx′，板簧和测力传感器的预紧位移为Δx，则有

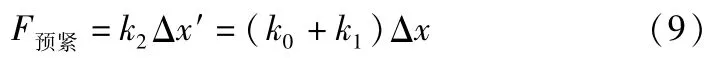
结合式（4）、式（8）和式（9），为了保证整个测试机构的刚度和强度，要求板簧刚度k0足够大；为了准确地测量不平衡量产生的离心力，测力传感器的安装刚度k1必须占总刚度较大比例，即提高系数α。所以可以选用刚度较小的预紧弹簧来提高系数α的值，使测量结果更加准确。由此应在满足刚度和强度的情况下，使k0与k1有相当量级，且k0＞＞k2，k1＞＞k2。

3 测量电路

测力传感器中的压电材料可以分为压电晶体、压电陶瓷和新型压电材料三类。石英类压电晶体的压电常数d11=2.31pC/N，而锆钛酸铅系压电陶瓷（PTZ）的压电常数是石英晶体的好几百倍，达到d33=200～500pC/N，所以选用PTZ作为测力传感器的材料更为合理。压电陶瓷产生的电荷量Q与外力F成比例关系，即Q=d33·F，其中d33为压电系数。

由于压电陶瓷制作的传感器的内阻很大，输出信号很微弱，所以要求负载电阻RL值必须很大。为了减小测量误差，通常把传感器的输出信号先接入一个高输入阻抗的前置放大器，然后再接入一般的滤波放大电路。前置放大器一般是电荷放大器。

根据文献［8］可知，电荷放大器的输出电压Uo与压电陶瓷产生的电荷量Q存在式（10）的关系

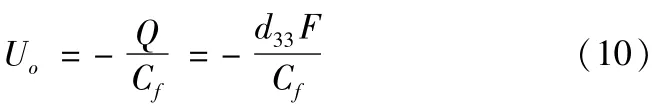
其中Cf为反馈电容。将式（4）代入式（10），得到输出电压Uo与测试转速ω之间的关系

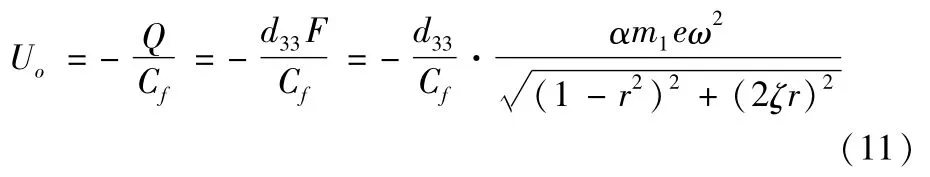
根据式（11）可知电荷放大器的输出电压Uo与电荷成正比，与不平衡激励力成正比，在不平衡量m1e一定时与转速ω的两次方成正比。

电荷放大器后接的滤波放大电路采用与文献［9］中类似的八阶有源带通滤波器。

4 设计案例

设计一台立式硬支撑平衡测试机，振动体的质量m0=31.2kg，旋转主轴盘的质量m1=5.4kg，测试转速范围为600～900rpm（10～15Hz）。在未安装传感器时测试的固有频率为71.7Hz，相当于板簧的横向刚度k0=7.42e6N/m。选用的预紧弹簧刚度k2=3.5e4 N/m，安装预紧量为6mm。加装传感器后，平衡测试机实测的固有频率提升到132.7Hz，这相当于传感器提供的安装刚度k1=18.0e6N/m，较板簧提供的主刚度k0大得多。系数α=k1/（k0+k1+k2）=0.71，为较好的刚度分配比。该平衡测试机设计的测量工件质量范围为小于20kg的盘状转子。当测量工件达到最大20kg时，其固有频率计算值为106.6Hz，实测值为104Hz。测试机的频率比r≤0.144，由式（6）计算的永久标定可产生的误差为2%。

在平衡测试机上进行数据测试，不平衡量则采用影响系数法来计算得到，步骤如下：①考察测试数据的重复性；②将测试机的初始不平衡量尽量减小；③在旋转频率10～15Hz的整频率点上测量平衡测试机输出的初始振动信号；④在旋转主轴盘的周向90°半径110mm的位置加3.182g的质量，相当于350gmm；⑤在10～15Hz的整频率上测量振动信号；⑥去掉3.18g的试重，在主轴盘的周向45°半径110mm的位置加5.80g的质量，相当于638gmm；⑦在10～15Hz的整频率点上测量振动信号。

步骤①中的数据见表1，步骤②～⑦的数据见表2。

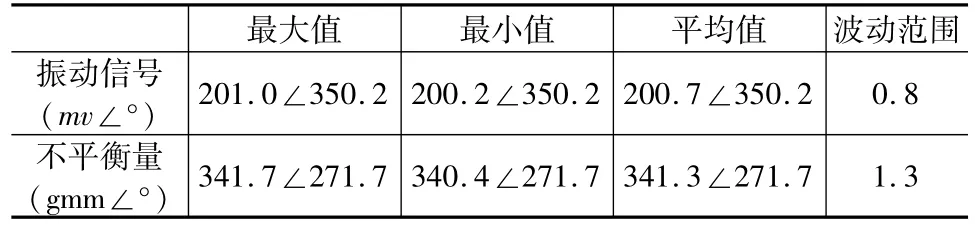
表1 同一不平衡量的多次测量数据

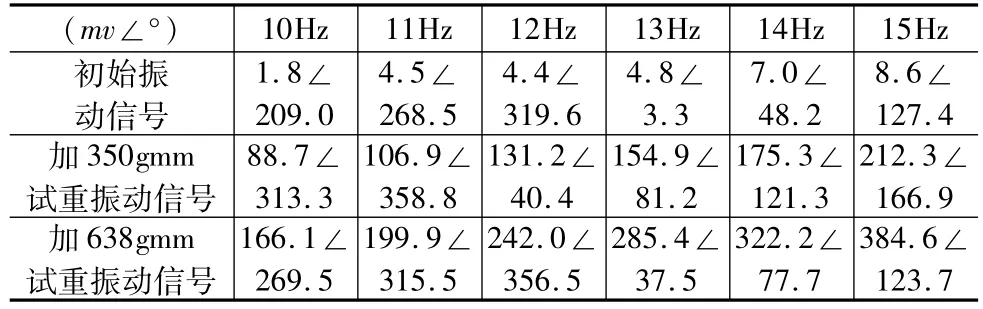
表2 不同转速下同一不平衡量的测量数据

4.1 测试数据的重复性

表1中的数据是在转速为900rpm（15Hz）时，对同一不平衡量产生的振动信号进行20次的测量，从中找出的最大值、最小值和平均值。用后续步骤得到的影响系数换算出来的不平衡量也示出作为参考。数据表明测试具有很好的重复性。

4.2 振动信号与转速关系

表2中两次加试重后的增量振动信号的幅值与转速频率间的关系如图3所示，图3中还包括对增量振动信号幅值进行二次曲线拟合后的曲线，其表达式见式（12）。可以看出振动信号幅值基本与不平衡量成正比，与转动频率的平方成正比；图中拟合曲线在测试点的相对误差都小于2%。

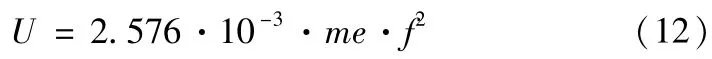
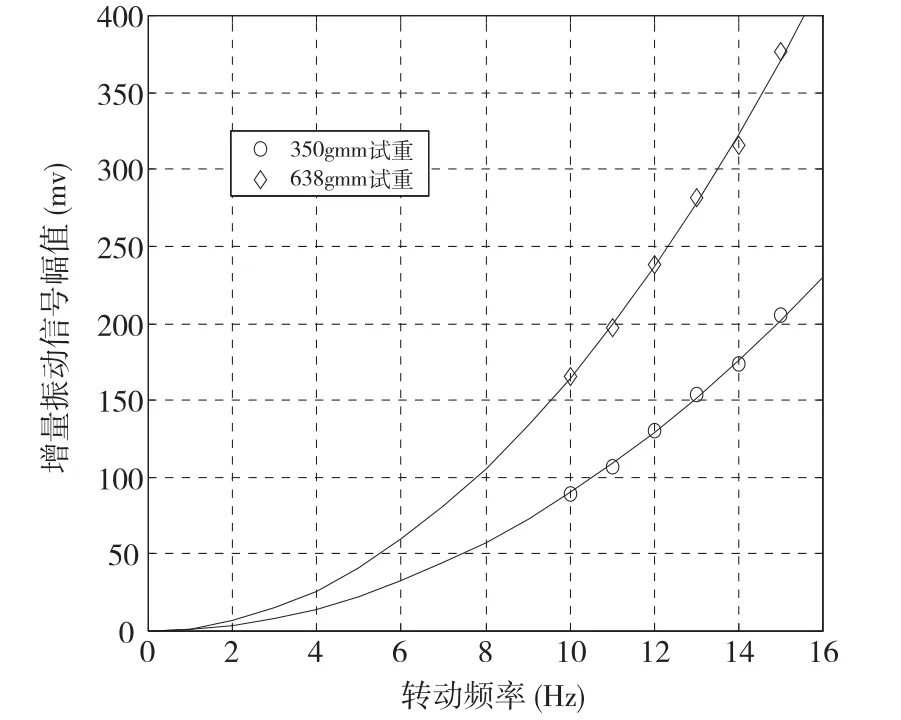
图3 增量振动信号幅值与转动频率的关系

4.3 永久标定分析

对表2中的数据进行进一步分析，得到表3数据。表3中：行①为表2中由初始振动信号和加350gmm试重振动信号计算的在不同转动频率下的影响系数；行②为由影响系数和初始振动计算得到的初始不平衡量；行③为由影响系数和加638gmm试重振动信号计算得到的测试不平衡量；行④为测试不平衡量与已知试重638gmm的误差率；行⑤为按15Hz转动频率永久标定后进行其他转动频率下的不平衡量测试数据；行⑥为永久标定时的误差率。

表3中的标定分析数据表明：按不同转动频率标定后进行的不平衡量测试，其精度误差率除10Hz在1.6%外，其他都小于1%；按15Hz转动频率永久标定后进行的不平衡量测试，其误差率在14Hz时最高达到3.3%。总体看来设计的立式硬支撑平衡测试机的测试精度较高，其原因为刚度配比系数α较大，达到了0.71，可产生信噪比高的信号。另外机器固有频率高使得频率比r较小，降低了永久标定的误差。

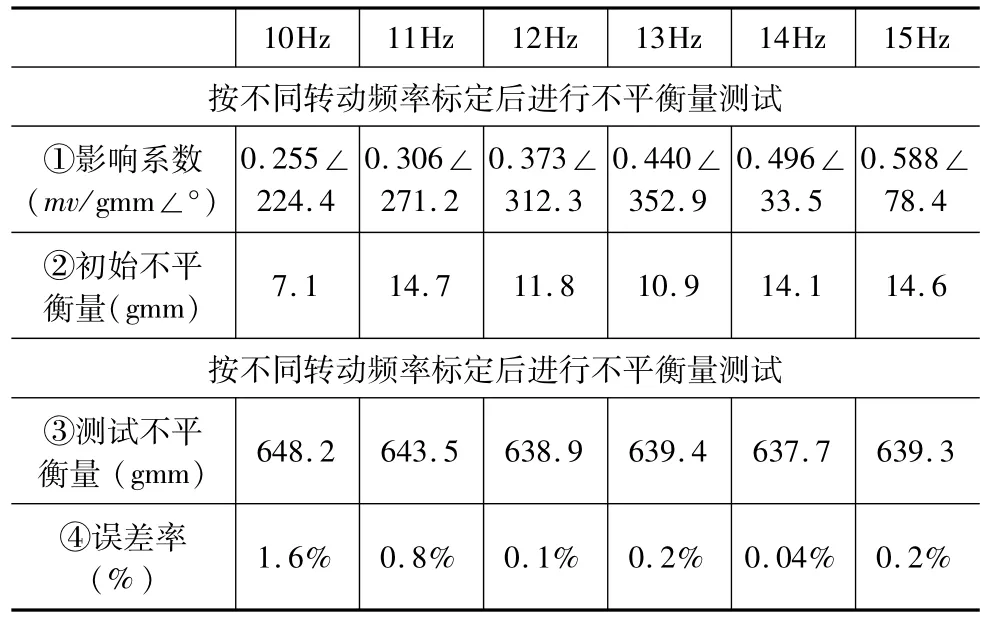
表3 标定分析

续表

5 最小可达剩余不平衡度emar

最小可达剩余不平衡度emar是平衡机能使转子达到的剩余不平衡量的最小值，为衡量平衡机平衡能力的指标，单位为gmm/kg或μm。文献［10］介绍了测量方法，归纳为：①采用规定的至少有8个均布螺纹孔的标准校验盘状转子，将其平衡到5emar以下；②根据所选标准校验转子的质量m1、试重安装半径r和被测平衡机预先估计最小可达剩余不平衡度emar指标，按式（13）计算试重10UPP；③用10UPP的试重分别加在标准校验转子的所有均布螺纹孔上，进行不平衡量测量，记录相应的不平衡量幅值Ui（g）和相位（°）；④计算Ui的算术平均值Umean；⑤如果所有的测试数据Ui都能满足0.88Umean＜Ui＜1.12Umean，则步骤②中预估的emar是合适的，否则需要重新估计emar并重复上述过程；⑥测试系统实际最小可达剩余不平衡度emar实际，可由式（14）来计算。

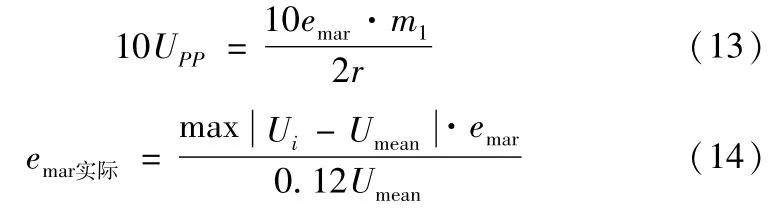
在试验机上确定转子的质量m1=12kg，预估emar为1μm，根据式（13）计算加重半径r=121.5mm上的试重10UPP=0.493g，实际取490mg。将试重加到转子的螺钉孔上，记录得到表4。由表4的数据分析可知，设计的平衡测试机最小可达剩余不平衡度为0.32μm，优于市场上可提供的大多数同类机器。

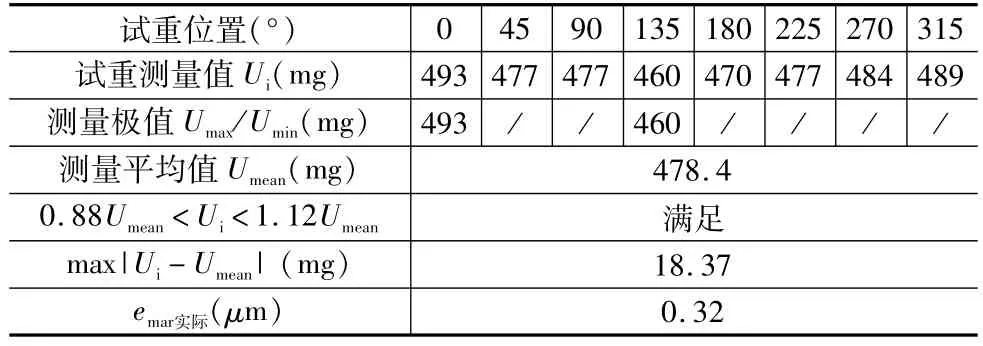
表4 最小可达剩余不平衡度emar测试数据

6 结束语

针对硬支撑动平衡测试机的设计，进行了机器的动力学研究，给出了板簧刚度、测力传感器安装刚度和预紧弹簧刚度的选取原则，分析了影响永久标定误差的因素，制作了样机，进行实验测试以及最小可达剩余不平衡度测定。工作表明，按照设计方法设计的测试机具有较高的测试精度。研究工作为立式硬支撑全自动平衡修正设备的研制打下了良好的基础。

［1］李顶根.新型立式动平衡机的研制与工件动不平衡量的测量［D］.武汉：华中科技大学，2004.

［2］钟沈江，许沧粟.立式硬支承动平衡机微机化测量系统的研究［J］.小型内燃机与摩托车，2003，32（3）：8-10，23.

［3］钟沈江.硬支承动平衡机微机化测量系统的研究［D］.杭州：浙江大学，2003.

［4］康成良，李慧敏，赵良梁，等.用于中小型电机转子的全自动平衡机的设计与实现［J］.组合机床与自动化加工技术，2007（2）：67-70.

［5］李常品，曾胜，康成良，等.四工位全自动转子平衡机的设计与实现［J］.制造技术与机床，2008（12）：89-92.

［6］程涛涛，曾胜.用于发动机曲轴的全自动平衡修正系统的设计研究［J］.组合机床与自动化加工技术，2012（8）：1-5.

［7］三轮修三，下村玄.旋转机械的平衡［M］.1版.北京：机械工业出版社，1980.

［8］李迎春，叶湘滨.传感器原理［M］.长沙：国防科技大学出版社，2004.

［9］曾胜，任意，李常品，等.一种可实现不平衡量快速测试的带通滤波器［J］.振动与冲击，2011，30（6）：36-40，66.

［10］于梅，于仲敏.平衡机最小可达剩余不平衡度测试方法的研究［J］.计量技术，2001（4）：16-18.

（编辑 赵蓉）

The Design Study of Single Plane Vertical Hard Bearing Dynamic Balancing Machine

LUO Di-wei，XIE Xuan，LI Bin，ZENG Sheng，GU Chao-hua
（Institute of Chemical Machinery，Zhejiang University，Zheda-Jizhi Research Centre，Hangzhou 310027，China）

In connection with the design of Single Plane hard bearing dynamic balancing measurement machine，a series of theoretical analysis was done，including the dynamics analysis of the machine，analyzing the factors influencing permanent calibration error and presenting a stiffness principle of spring board，sensor and preloaded spring.After this，the experiments of testing and minimum achievable residual unbalance are done with a prototype designed by the design scheme.The result demonstrates that the prototype has high measurement precision.

hard bearing；balancing measurement machine；stiffness proportion；permanent calibration

TH122；TG65

A

1001-2265（2015）06-0053-05 DOI：10.13462/j.cnki.mmtamt.2015.06.015

2014-09-15；

2014-10-21

罗迪威（1989—），男，浙江慈溪人，浙江大学化工机械研究所硕士研究生，研究方向为全自动平衡修正技术，（E-mail）luodiwei@zju.edu.cn；通讯作者：曾胜（1970—），男，江西全南人，浙江大学化工机械研究所研究员，博士，研究方向为全自动平衡修正技术，（E-mail）shengzeng@zju.edu.cn。