驱动桥主减速器齿轮多目标优化研究*

王丰元，程 明，杨朝会，纪建奕

（1.青岛理工大学汽车与交通学院，山东青岛 266520；2.青特集团有限公司技术中心，山东青岛266106）

驱动桥主减速器齿轮多目标优化研究*

王丰元1，程 明1，杨朝会2，纪建奕2

（1.青岛理工大学汽车与交通学院，山东青岛 266520；2.青特集团有限公司技术中心，山东青岛266106）

针对驱动桥主减速器齿轮研究，以主减速齿轮传动效率、传递扭矩能力和重合度为目标函数，建立了主减速器齿轮传动多目标优化数学模型，采用带精英策略的快速非支配排序遗传算法（NSGA-II），对主减速器齿轮传动进行了优化设计，得到了pareto最优解，从中选择了一个优化方案与原始设计方案进行对比，结果显示主减速器齿轮的传动效率有明显增加，传递扭矩能力和重合度都有一定的提升。

驱动桥；主减速器；多目标优化

0 引言

驱动桥主减速器是车辆传动系的重要组成部分，具有增矩减速的功用，有时还拥有改变转矩旋转方向的作用（发动机纵置）。随着主减速器技术逐渐进步、驱动桥市场用户需求等多方面综合因素的影响，汽车主减速器总体向着六高、二低、二化方向发展，即高承载、高精度、高齿面硬度、高可靠性、高速度、高传动效率，低成本、低噪声、标准化、多样化。在目前的中重型汽车驱动桥主减速器上，“格里森”（Gleason）制或“奥利康”（Oerlikon）制螺旋锥齿轮和双曲面齿轮等类型被广泛采用［1］。通常齿轮的传动效率与其功率损失成反比，它是评价齿轮传动质量的一个重要指标，其值可表示能耗程度且与用户经济利益相关；当齿轮传动效率低（齿轮功率损失大），齿轮啮合会产生大量的热量使主减速器润滑油温度急剧升高，破坏润滑系统，导致齿轮失效（齿面磨损、点蚀和胶合等）［2］。Sivakuma P等［3］对齿轮重合度进行相关试验，试验结果显示低重合度齿轮比高重合度齿轮的寿命短、振动和噪声大。快速非支配排序遗传算法（A Fast ElitistNon-dominated Sorting Genetic Algorithm NSGA-Ⅱ），是Deb和Pratap等人针对非支配排序遗传算法（Non-dominated Sorting Genetic Algorithm，NSGA）的不足进行改进［4］。作者在综合考虑齿轮传动效率最大、齿轮接触强度计算许用功率最大和齿轮重合度最大三者关系的基础上，采用带精英策略的快速非支配排序遗传算法（NSGA-II）对主减速器齿轮进行多目标优化，该方法是一种基于Pareto最优解概念的遗传算法，优化的结果是得到一个非劣解集，设计者可以根据设计目标选择合适的方案，以达到设计要求。

1 优化设计数学模型建立

1.1 目标函数建立

现代中重型汽车驱动桥主减速器的性能不断提高，对主减速齿轮提出了更高的要求。作者基于齿轮的传动功率损失、传递扭矩能力、以及传动平稳性和可靠性等研究，建立齿轮传动效率最大、传递扭矩最大和重合度最大三个目标函数。

1.1.1 主减速齿轮传动效率最大

目前国内外主要有两种方法可以计算弧齿锥齿轮和双曲面齿轮的啮合效率：①威尔斯·柯勒曼提出的锥齿轮传动效率计算公式；②根据格里森尺寸卡给出的齿轮效率值经过转换得到不同载荷下的齿轮传动效率［5］。作者在前两种计算方法基础之上，采用解析法，分别求出齿轮啮合时的各种损失。

驱动桥主减速器齿轮啮合功率损失可近似认为主要由齿轮的滑动摩擦功率损失和齿轮的滚动摩擦功率损失，则主减速齿轮总的功率损失为齿轮的滑动摩擦和滚动摩擦功率损失之和。

主减速齿轮的滑动摩擦功率损失［6］：

齿轮滚动摩擦损失：

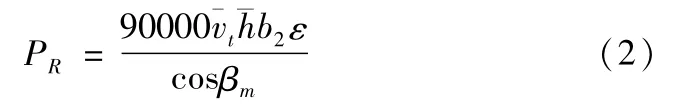
第一目标函数为：

1.1.2 主减速齿轮传递扭矩最大

为使主减速齿轮的传递扭矩大，应使主动齿轮接触强度计算的许用功率最大［7-8］，建立第二目标函数为：

式中：n1为主动齿轮转速；σHP为主动齿轮许用接触应力；dvm1为主动齿轮齿宽中点处锥齿轮当量齿轮的节圆直径；dm1为主动齿轮齿宽中点处节圆直径；ZH为节点区域系数；ZE为材料弹性系数；ZK为锥齿轮系数；Zεβ为接触强度计算的重合度与螺旋角系数；KA为使用系数；KV为动载系数；KHα、KHβ为接触强度计算的寿命系数和尺寸系数；ZLVR为润滑油膜影响系数；ZW为工作硬化系数；SHmin为接触强度的最小安全系数；σHlim为齿轮的接触疲劳极限应力。

1.1.3 重合度最大

重合度是评价齿轮传动质量的一项重要指标，齿轮采用高重合度设计可以减小传动时的振动和噪声，降低齿轮的动应力［9］。单对锥齿轮传动的重合度计算公式为：

端面重合度εα：

纵向重合度εβ：

第三目标函数为：

式中：αt为端面分度圆压力角；αvat1、αvat2为主、从动齿轮端面当量齿轮分度圆压力角；δ1、δ2为主、从动齿轮分锥角；βm为齿宽中点处螺旋角；b为齿轮齿宽（取主、从动齿轮齿宽最小）；mnm为锥齿轮中点法向模数。

2 设计变量

当驱动桥的工况和主减速器速比确定，主减速齿轮的传动效率、重合度和强度受齿轮端面模数m、主动齿轮齿数z1、从动齿轮齿数z2、齿宽系数ΦR、从动齿轮齿宽b2、齿轮中点螺旋角βm、主动齿轮变位系数x1等参数的影响。故优化设计变量为：

3 约束条件的确定

设计变量X的约束条件可以分为两大类：几何约束，如尺寸约束，形状约束等；性能约束，如应力约束。表1为设计变量的约束条件［10］。

表1 约束条件

4 优化方法

多目标优化问题（Multi-objective Optimization Problem，MOP），又称向量优化问题（Vector Optimiza-tion Problem），多准则优化问题（Multi-criteria Optimization Problem）或多性能优化问题［11］（Multi-performance Optimization Problem）。

大多数传统的多目标优化方法是将多个目标通过某种技术转换为一个目标的优化问题，然后再借助数学规划工具求解，将多目标转化为单目标通常需要人为设置一些参数，具有很大的主观性。一般情况下，多目标优化问题的各个子目标之间大多相互联系、制约，甚至互相矛盾，很难找到一个最优解使得不同的子目标同时达到最优。因此，对于多目标优化问题，往往存在一个折中解集合，对所有目标函数而言无法对解集中的解进行优劣比较，这样的解为非支配解（Non-dominated solutions）或Pareto最优解（Pareto Optimal solutions）。

NSGA算法是Srinivas和Deb于1995年提出的一种基于Pareto最优概念的多目标演化算法。NSGA在处理问题时存在计算复杂度高、需要人为指定共享半径等一些问题。针对NSGA算法的不足，Deb和Pratap等人对其进行了改进，并在其基础上提出了NSGA-Ⅱ算法。NSGA-Ⅱ与NSGA相比降低了算法的复杂度；其采用了拥挤度和拥挤度比较算子，代替了人为指定的共享半径，并在快速排序后采用拥挤度比较算子作为个体优胜劣汰的标准，使种群中的个体均匀分布到整个Pareto域，保持了种群的多样性；引入了精英策略，将父代与其子代种群进行组合，参照分布度和适应度选择更加优良的下代种群，使优良的个体不会被丢弃，并提高种群的水平。NSGA-Ⅱ算法流程如图1所示。

图1 NSGA-Ⅱ算法流程图

5 优化实例

作者对457车桥主减速齿轮传动进行优化，输入功率P=202kW，输入转速n1=1657r/min，主减速比i=4.44，主、从动锥齿轮材料20CrNiMo。

采用MATLAB软件中提供的函数gamultiobj，对驱动桥主减速器齿轮进行多目标优化。其中，函数gamultiobj是NSGA-Ⅱ的一种改进算法。对函数gamultiobj的参数进行设置：种群大小为150，最优前段个体系数为0.2，最大进化代数和停止代数都为200。经过200代优化，得到Pareto最优解集，根据设计目标从中选出一组优化方案与原始设计进行对比，如表2所示。

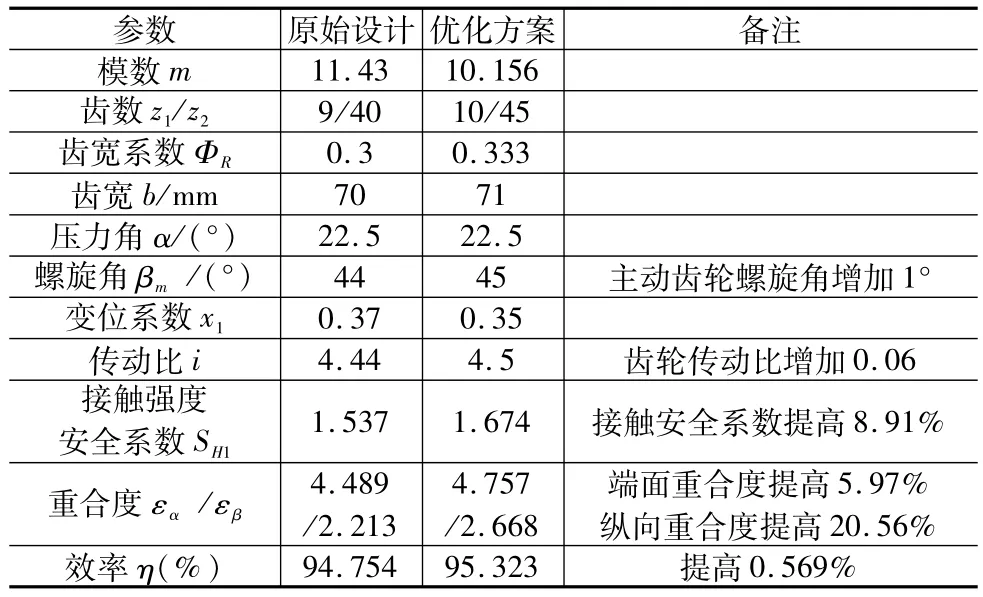
表2 优化前后参数对比

根据威尔斯·柯勒曼等对弧齿锥齿轮和双曲面齿轮效率的研究可知，齿轮螺旋角和传动比是齿轮效率的主要影响因素。由表2中数据知，优化后主减速器齿轮的一些结构参数发生了改变，其中主动齿轮中点螺旋角增加1°，齿轮传动比增加0.06，主减速齿轮效率提高了0.569%；与原始方案相比，优化后主减速齿轮的重合度和强度有一定的提高，尤其是纵向重合度，其值提高了20.56%，齿轮接触强度安全系数提高了8.91%。优化结果表明，对主减速齿轮进行优化使齿轮传动效率、传递扭矩和重合度达到最大是可行的。

6 结论

基于NSGA-II算法，综合考虑主减速齿轮传动效率、传扭能力和重合度等性能，建立驱动桥主减速器齿轮多目标优化设计的数学模型并进行优化。通过实例求解，体现了该方法的可行性。主减速齿轮多目标优化结果表明，多目标优化可以使多个优化目标同时达到最优化，从而得到高效率、高承载、高重合度的主减速齿轮。

［1］刘惟信.汽车车桥设计［M］.北京：清华大学出版社，2004.

［2］周哲波.弹流润滑状态下齿轮啮合效率的研究［J］.机械设计，2004，21（12）：40-43.

［3］Sivakuma P，Gopinath K，Sundaresh S.Performance evaluation of high-contact-ratio gearing for combat tracked vehicles-a case study［J］.Automobile Engineering，2009，224（5）：631-643.

［4］Kalyanmoy D，Amrit P，Sameer A，et al.A fast and elitist multiobjective genetic algorithm NSGA-II［J］.Evolutionary Computation，2002，6（2）：182-197.

［5］北京齿轮厂.格利森技术资料译文集：第二分册［M］.北京：机械工业出版社，1983.

［6］朱颖.锥齿轮传动箱效率计算方法比较研究［J］.机床与液压，2005（5）：63-64.

［7］梁华琪.弧齿锥齿轮传动的多目标优化设计［J］.现代机械，2004（6）：18-20.

［8］于广滨.航空用微小型减速装置多目标优化设计及性能分析［D］.哈尔滨：哈尔滨工业大学，2009.

［9］赵宁，杨杰.高重合度圆柱齿轮传动多目标优化设计［J］.机械传动，2012.36（7）：43-46.

［10］闻邦椿.机械设计手册［M］.北京：机械工业出版社，2010.

［11］马小姝，李宇龙，严浪.传统多目标优化方法和多目标遗传算法的比较综述［J］.电气传动自动化，2010，32（3）：48-50.

（编辑 赵蓉）

Study on Multi-objective Optimization of Drive Axle Main Reducer Gear

WANG Feng-yuan1，CHENG Ming1，YANG Chao-hui2，JI Jian-yi2
（1.School of Automobile and Transportation，Qingdao Technological University，Qingdao Shandong 266520，China；2.Center of Technique，Qingte Group Limited Corporation，Qingdao Shandong 266106，China）

Multi-objective optimization model of main reducer gear is established with efficiency of main reducer gear，torque transmission capability and degree of coincidence as objective function for drive axle main reducer gear，a fast elitist non-dominated sorting genetic algorithm（NSGA-II）is adopted.Optimized design has been carried out on main reducer gear，pareto optimal solution is obtained.An optimization scheme is chosen to compare with the original design，the results show that transmission efficiency of main reducer gear has been increased significantly，transmission torque capacity and degree of coincidence have been improved.

drive axle；main reducer；multi-objective optimization

TH132.422；TG506

A

1001-2265（2015）06-0033-03 DOI：10.13462/j.cnki.mmtamt.2015.06.009

2014-09-18；

2014-10-23

山东省科技攻关项目（2011GGX10317）

王丰元（1963—），男，山东青岛人，青岛理工大学教授，博士，研究方向为智能交通与智能车辆，（E-mail）fy58wang@126.com；通讯作者：程明（1991—），男，山东青岛人，青岛理工大学硕士研究生，研究方向为车辆现代设计理论，（E-mail）chengming636@126.com。