考虑开槽和高次谐波的永磁同步电机解析模型*

2015-11-03马琮淦左曙光

振动、测试与诊断 2015年2期

关键词：永磁体气隙同步电机

马琮淦，左曙光，孟　姝，孙　庆

（同济大学新能源汽车工程中心上海，201804）

考虑开槽和高次谐波的永磁同步电机解析模型*

马琮淦，左曙光，孟姝，孙庆

（同济大学新能源汽车工程中心上海，201804）

永磁同步电机6i阶（i∈N）转矩波动是电机总成与电动车车身阶次振动的主要振源。笔者提出了一种考虑定子开槽与高次谐波的永磁同步电机解析计算模型。建模过程基于瞬态气隙磁场分布的计算。当不考虑电流谐波时，电磁转矩具有6i阶（i∈N）转矩波动特性。最后，通过有限元计算验证了该解析计算结果。文中解析模型揭示了电动车用永磁同步电机转矩波动非线性的形成机理。

开槽；高次谐波；永磁同步电机；电动车；解析模型

引言

永磁同步电机（permanent magnet synchronous motors，简称PMSM）具有高功率密度和宽调速范围，被广泛应用于电动汽车的直接驱动。然而，其6i阶（i∈N）转矩波动造成了电机总成和电动汽车车身的阶次振动［1-2］。因此，研究永磁同步电机转矩波动是十分必要的。

当假设电枢绕组中通入正弦电流时，主要有两种因素引起转矩波动［3］：定子开槽和高次谐波。因此，在转矩波动的计算中应当考虑定子开槽引起的磁导变化和由永磁体产生的高次谐波。对于转矩波动的分析，Ree等［4］假设气隙磁场已知，提出了一种研究表贴式和内埋式永磁同步电机齿槽转矩和电磁转矩波动的方法；Takeo Ishikawa等［5-6］用有限元法分析了齿槽转矩和电磁转矩的总和；文献［7］提出了一种考虑电磁饱和参数来减小转矩波动的方法；文献［8］采用了一种两步设计过程，通过二维有限元分析减小转矩波动；为避免冗长的有限元分析计算，文献［9］提出了一种永磁电机解析建模方法；文献［10］分析了两种减小永磁同步电机伺服驱动转矩波动的方法。然而，绝大多数永磁同步电机控制系统都是基于不考虑开槽、高次谐波的永磁同步电机线性模型，不能反映电动车用永磁同步电机转矩波动非线性特性。

为此，笔者提出了一种考虑定子开槽和高次谐波的永磁同步电机非线性解析模型。所获得的转矩波形与二维有限元分析计算的波形吻合，证明了本解析法的准确性。

1 考虑开槽的永磁体磁场分布

本模型做了如下假设：a.忽略电磁饱和、磁滞和涡流的影响，电机为线性的磁性条件；b.电机电流为对称的三相正弦规律变化；c.定子开槽，槽是矩形或梯形。

定子开槽会导致磁路中磁导的变化，磁导会影响永磁体磁场的分布。开槽磁导依赖于转子位置，磁场波形也是随着转子位置变化的。为了获得气隙内永磁体磁场分布，笔者采用了与文献［11］中相似的方法。据文献［11］作者的观点，气隙内永磁体径向磁场分布可通过忽略定子开槽时永磁体磁场与气隙开槽时相对磁导的乘积求得：

其中：BPM-less（θ1）为不开槽定子的磁场分布函数；α为转子表面的角度；θ为转子位移角；θ1为相对于转子的角度；λ（α）为开槽气隙区域的相对磁导函数。

不开槽定子瞬态磁场分布函数BPM-less（θ1）的计算见文献［12］。在极坐标下通过求解气隙磁场的泊松方程组，当时，气隙内永磁体径向磁场分布为

其中：Br为永磁体材料的剩磁，αp为极弧系数；p为极对数；Rm为永磁体圆弧半径；Rr为转子铁心圆弧半径；Rs为定子铁心圆弧半径；r=Rs+g/2；μr为永磁体相对磁导率；B2i-1为磁场第（2i-1）次谐波幅值。

开槽以两种方式影响磁场。首先，减少了每极磁通，通常通过引入卡特系数kc计算此效应。其次，影响永磁体和气隙内的磁场分布。笔者采用文献［11］中开槽气隙区域的二维模型相对磁导函数λ（α）来计算，可推得：

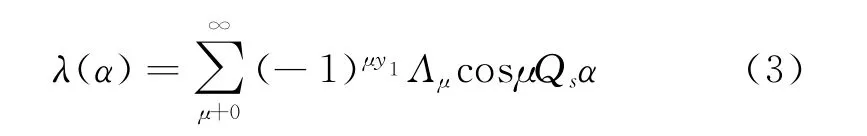
其中：y1为绕组节距；Qs为槽数。

Λμ的推导如下：

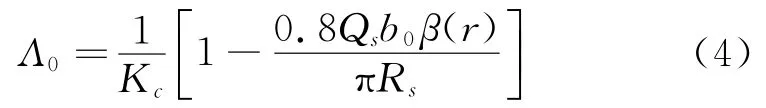
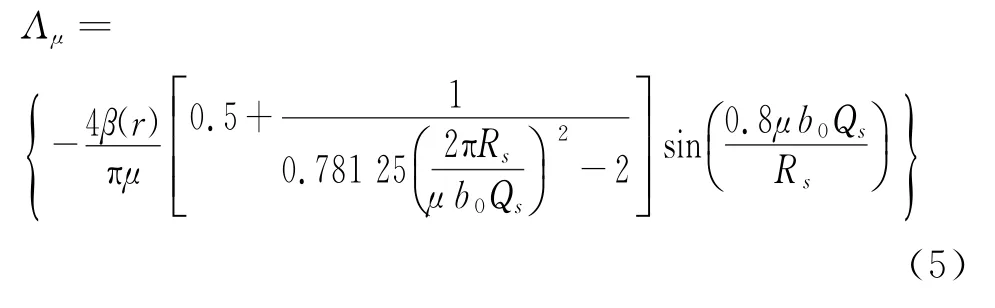
其中：b0为槽宽度。

卡特系数kc近似为

其中：g为气隙长度，hm为永磁体厚度。

β（r）可通过保角变换获得：

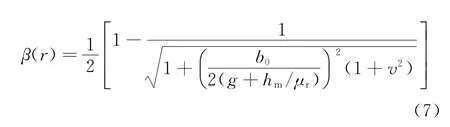
其中，各参数可通过如下方程确定：

式（8）是一个包含对数函数、指数函数和反三角函数的超越方程。笔者提出了通过牛顿下山法解此超越方程。首先假设：

其次，求得f（v）的导数：

根据牛顿下山法，式（8）的迭代解vk+1计算如下：

因此，式（1）中气隙内永磁体径向磁场分布的解析解如下：

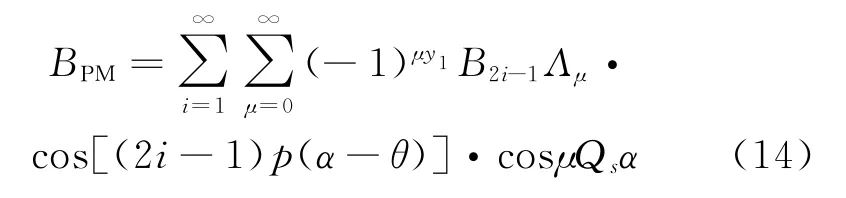
2 定子的总磁链

根据电机学，定子总磁链由两个部分组成。一部分是永磁体磁场产生的磁链；另一部分是电枢磁

场产生的磁链。可表示如下：

其中：Ψtotal，dq为定子总磁链矩阵；Ψmagnet，dq为由永磁体磁场产生的磁链矩阵；Ψarmature，dq为电枢磁场产生的磁链矩阵。

2.1永磁体磁场产生的磁链

为计算永磁体磁场在a相绕组中的磁链，用到磁链标准计算式：

其中：ψ为磁链；B为磁场分布；s为面积。

因此，永磁体磁场在a相绕组中产生的磁链为

其中：ψm，a（θ）为永磁体磁场在a相中产生的磁链；kd（2i-1）为绕组第（2i-1）次谐波分布系数；Nc为一相绕组串联匝数；αj为绕组节距角；ls为定子长度。

假设［13］：

其中：q为每极每相槽数；m为相数；b为一个整数；c/d为一个不可约真分数。

因此，根据文献［13］，可得到适用于整数槽绕组和分数槽绕组的第（2i-1）次谐波分布系数kd（2i-1）：

给出一相绕组串联匝数Nc：其中：C1为绕组层数；Nk为每槽每层导体数；a1为并联支路数。

将式（21，22）代入式（17），得式（17）的解析解为

其中：当时（2i-1）p-μQs≠0时，

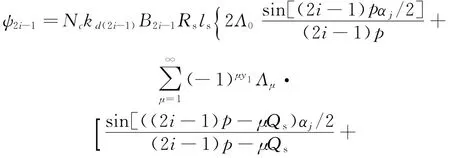
当时（2i-1）p-μQs=0时，

因此，永磁体在a，b，c相中产生的磁链矩阵Ψm，abc为

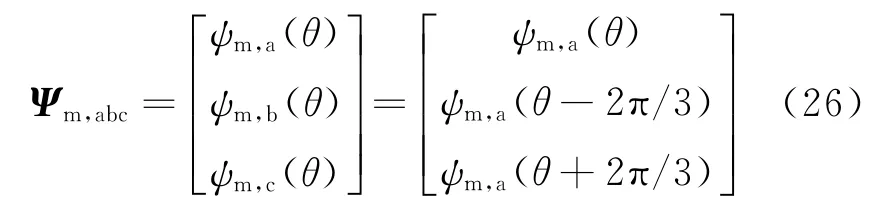
故，dq坐标系下永磁体产生的磁链矩阵Ψmagnet，dq可通过Blondel-Park变换矩阵Tdq，abc求得：

2.2电枢磁场产生的磁链

电枢磁场产生的磁链矩阵Ψarmature，dq可由下式求得：

其中：Ld为d轴电感；Lq为q轴电感；id为d轴电流；iq为q轴电流。

假设相电流矩阵为

其中：ia，ib，ic分别为a，b，c相电流；imax为电流幅值；φ为内功率因数角。

因此，可得id和iq：

2.3定子总磁链

定子总磁链可由永磁体磁场产生的磁链与电枢磁场产生的磁链求和求得。式（15）的解析解为

其中：ψ1，ψ（6i-1）和ψ（6i+1）可由式（24，25）确定。

3 计算电压

定子相电压用矩阵的形式可表示为

其中：rs为相电阻，ψabc为a，b，c相绕组的总磁链矩阵。

注意到通过Blondel-Park变换矩阵Tdq，abc可以将相向量转换为相应的dq坐标系下的向量。因此，式（30）两边同时乘以Tdq，abc，可转换为

在一些繁复的推导后，式（33）可表达为

其中：ωr为转子电角速度。式（34）的解析解变为

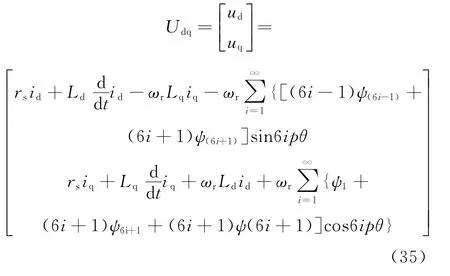
因此，可得感应电动势Edq：

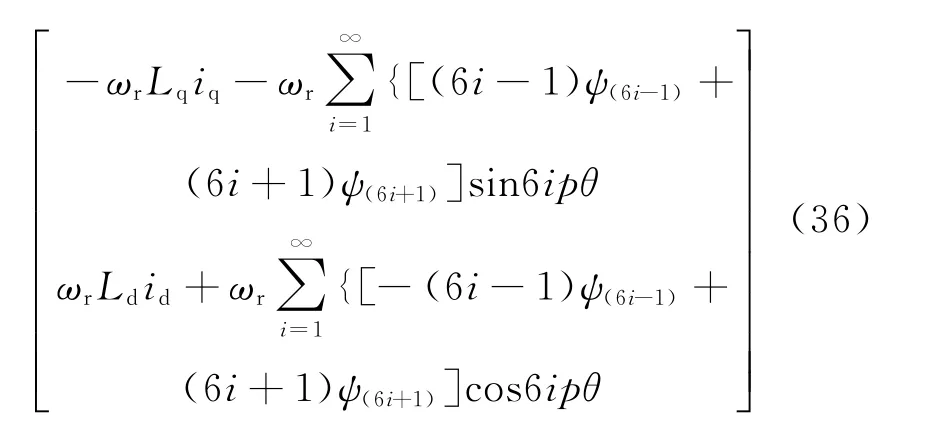
4 6i阶转矩波动计算与频率分析

4.16i阶转矩波动计算

电磁功率Pem用矩阵形式可表达为

可得电磁转矩：

其中：ωm为转子机械角速度。

电磁转矩的解析解为

机械运动方程表达如下其中：J为转子总的转动惯量；TL为负载转矩；B为摩擦系数。

4.2波动频率分析

根据式（39），当假设电枢绕组通入正弦电流时，电磁转矩波动由两部分6i阶波动项组成均由永磁体磁场谐波产生。因此，转矩波动频率为

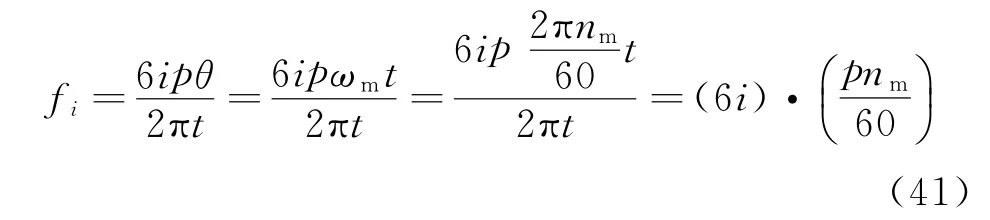
其中：nm为转速；t为时间。

结果表明：电磁转矩具有6i阶波动特性。这从理论上解释了永磁同步电机总成和电动汽车车身的阶次振动。在设计电动汽车时，为避免共振，电机总成与车身的结构模态频率应当远离6i阶转矩波动频率。因此，笔者为电动汽车的模态频率规划提供了理论基础。

5 永磁同步电机动态模型

综上所述，考虑定子开槽和高次谐波的永磁同步电机的动态模型可由以下3个方程表示：

其中：当（2i-1）p-μQs≠0时，

当（2i-1）p-μQs=0时，

6 解析计算结果与有限元分析结果的比较

笔者基于以上解析模型，编制计算机软件［14］，应用该软件对解析模型和有限元模型进行了比较。计算实例选择了用在电动车上的三相20极27槽双层绕组永磁同步电机。该电机的主要参数见表1，电机模型见图1。在计算前，运用本解析模型可以预测转矩谐波频率为

表1　计算实例电机的主要参数Tab.1 Main parameters of the prototype SPMSM

图1　计算实例电机横截面Fig.1 Cross-section of the SPMSM

图2　气隙磁密对比Fig.2 Comparison with FEA for permanent magnet field in the air gap

解析模型和有限元法计算出的气隙磁密如图2所示，气隙磁密谐波幅值如图3所示。根据图3，除了第17阶的磁通谐波B17之外，解析模型结果能较好吻合有限元模型结果。根据式（24）和（25），上述差异会导致解析模型和有限元模型的17阶磁链Ψ17存在差异。再根据式（39），其后果是：本解析模型与有限元模型中，第3阶转矩谐波Tem-3将存在一定的差异。

图3　气隙磁密谐波阶次特性对比Fig.3 Comparison with FEA for the amplitude-order characteristic of permanent magnet field in the air gap

从图4、图5可以看出，除了第3阶转矩谐波之外，通过解析模型计算出的转矩谐波频率与幅值和用有限元方法计算出的结果基本一致。原因是解析模型与有限元模型的第17阶磁密谐波计算差异造成的第17阶磁链偏差。然而，第3阶转矩谐波比第1阶转矩谐波要小很多，因此，解析模型的精度仍旧较高。从上面的分析可以看出，该解析模型的准确性主要取决于气隙磁密的计算精度。

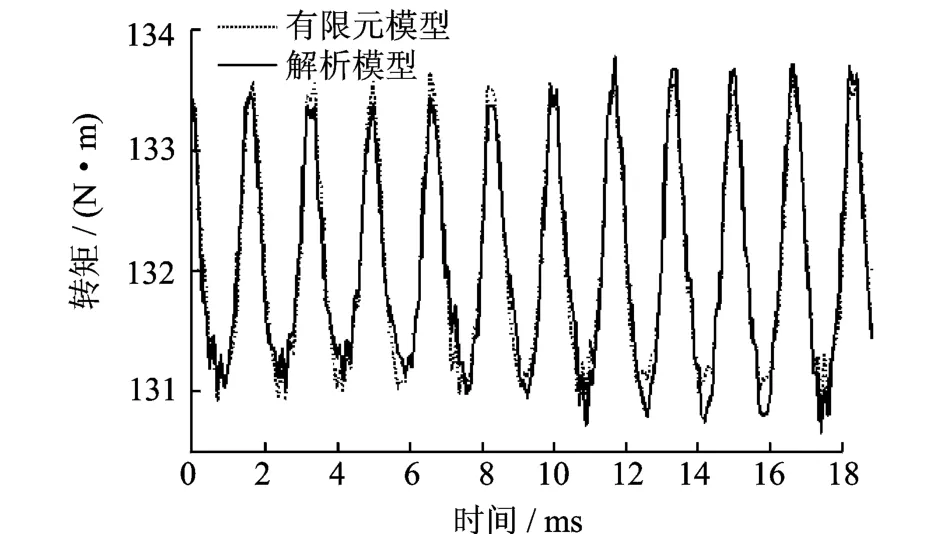
图4　转矩波动对比Fig.4 Comparison with FEA for the torque ripple

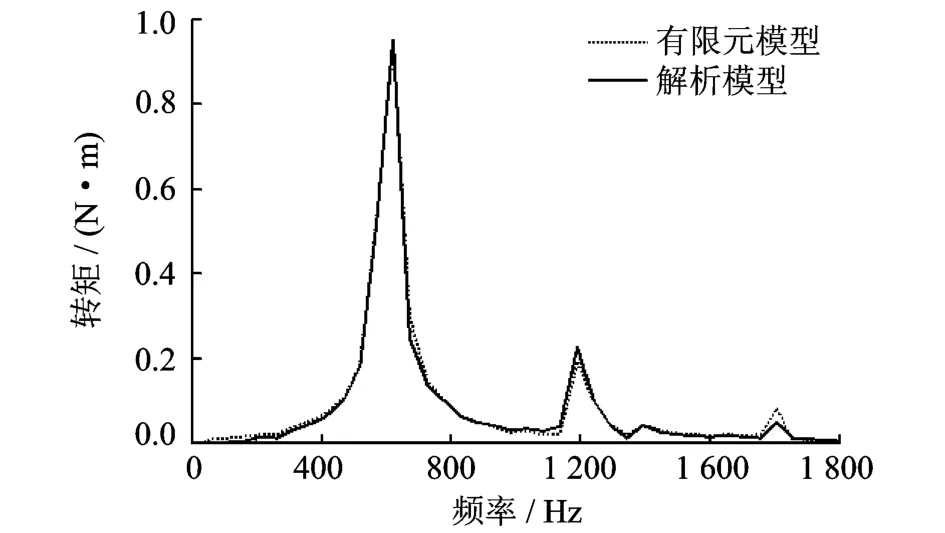
图5　转矩谐波幅频特性对比Fig.5 Comparison with FEA for frequencies and amplitudes of torque harmonics

7 结束语

笔者提出了一种考虑定子开槽和高次谐波的永磁同步电机6i转矩波动非线性解析模型。用这个解析模型，预测了6i阶转矩波动并分析了波动频率。这从理论上解释了电机总成与电动车车身阶次振动的振源特性。

［1］王建，张立军，余卓平，等.燃料电池轿车电机总成的振动阶次特征分析［J］.汽车工程，2009，31（3）：219-223. Wang Jian，Zhang Lijun，Yu Zhuoping，et al.An analysis on the vibration order feature of the electric motor assembly in a fuel cell car［J］.Automotive Engineering，2009，31（3）：219-223.（in Chinese）

［2］马琮淦，左曙光，何吕昌，等.电动车用永磁同步电机电磁转矩的解析计算［J］.振动、测试与诊断，2012，32（5）：756-761. Ma Conggan，Zuo Shuguang，He Lüchang，et al.Analytical calculation of electromagnetic torque in permanent magnet synchronous motor for electric vehicles［J］.Journal of Vibration，Measurement and Diagnosis，2012，32（5）：756-761.（in Chinese）

［3］ Borghi C A，Casadei D，Cristofolini A，et al.Minimizing torque ripple in permanent magnet synchronous motors with polymer-bonded magnets［J］.IEEE Transactions on Magnetics，2002，38（2）：1371-1377.

［4］ de Ree J.la，Boules N.Torque production in permanent-magnet synchronous motors［J］.IEEE Transactions on Industry Appliactions，1989，25（3）：107-112.

［5］ Ishikawa T，Yamada M，Kurita N.Design of magnet arrangement in interior permanent magnet synchronous motor by response surface methodology in consideration of torque and vibration［J］.IEEE Transactions on Magnetics，2011，47（5）：1290-1293.

［6］ Ishikawa T，Slemon G R.A method of reducing ripple torque in permanent magnet motors without skewing［J］.IEEE Transactions on Magnetics，1993，29（2）：2028-2031.

［7］ Kim K S，Lee H，Kim K，et al.Torque ripple improvement for interior permanent magnet synchronous motor considering parameters with magnetic saturation［J］.IEEE Transactions on Magnetics，2009，45（10）：4720-4723.

［8］ Borghi C A，Casadei D，Cristofolini A，et al.Application of a multiobjective minimization technique for reducing the torque ripple in permanent-magnet motors［J］.IEEE Transactions on Magnetics，1999，35（5）：4238-4246.

［9］ Proca A B，Keyhani A，EL-Antably A，et al.Analytical model for permanent magnet motors with surface mounted magnets［J］.IEEE Transactions on Energy Conversion，2003，18（3）：386-391.

［10］Colamartino F，Marchand C，Razek A.Torque ripple minimization in permanent magnet synchronous servodrive［J］.IEEE Transactions on Energy Conversion，1999，14（3）：616-621.

［11］Zhu Z Q，Howe D.Instantaneous magnetic field distribution in brushless permanent magnet dc motors，part 3：effect of stator slotting［J］.IEEE Transactions on Magnetics，1993，29（1）：143-150.

［12］Zhu Z Q，Howe D，Bolte E，et al.Instantaneous magnetic field distribution in brushless permanent magnet dc motors，part I：open-circuit field［J］.IEEE Transactions on Magnetics，1993，29（1）：124-135.

［13］李发海，朱东起.电机学［M］.北京：科学出版社，2007：192-194.

［14］马琮淦，左曙光，林福.考虑定子开槽和转子谐波的表贴式永磁同步电机电磁转矩快速计算软件：中国，2012SR086246［P］.2012-09-12.