基于LMI的两轮自平衡机器人控制器设计

方　辉

(渤海大学 工学院, 辽宁 锦州 121013)



基于LMI的两轮自平衡机器人控制器设计

方辉

(渤海大学 工学院, 辽宁 锦州 121013)

针对两轮自平衡机器人系统,提出基于线性矩阵不等式的控制器设计方法。首先,采用状态空间模型对两轮自平衡机器人系统进行描述。然后,通过线性矩阵不等式进行控制器的设计,并通过Lyapunov函数证明该方法的有效性,分析了基于观测器的控制器存在条件。最后,通过仿真进一步验证了该控制方法的有效性。

两轮自平衡机器人系统; 线性矩阵不等式(LMI); Lyapunov函数

0　引　言

两轮自平衡机器人由于其具有的工程应用价值,越来越多地引起相关研究人员的广泛关注。该系统实际上可看作是具备行走功能的一级倒立摆,保持平衡的过程实质是一个动态调节过程,即系统在平衡点附近不断地进行调节以保证平衡。文献[1]中,在对两轮自平衡机器人系统进行数学建模的基础上,基于LQR控制器方法实现对该系统的控制。文献[2]研究两轮自平衡机器人运动规律,并利用拉格朗日方程法建立动力学模型,通过自适应控制算法设计该系统的自平衡控制器。文献[3]通过LQR和龙伯格极点配置的方法对两轮自平衡机器人系统进行控制,得到较为稳定的动态平衡过程。文献[4]应用最优控制相关理论方法和两轮差动控制方法，设计了两轮自平衡机器人系统的控制器。目前,在控制系统设计中,系统稳定性的主要理论基础是Lyapunov稳定性理论,随着求解凸优化问题内点法的提出,线性矩阵不等式(LMI)技术在控制领域得到广泛应用。许多控制问题可以通过分析其线性矩阵不等式系统的可行性问题解决。随着MATLAB推出的求解矩阵不等式问题的LMI工具箱,从而使得处理、求解线性矩阵不等式的过程更加有效,大大促进了线性矩阵不等式技术方法在控制领域中的应用。鉴于上述分析,笔者针对两轮自平衡机器人系统,通过LMI技术,利用Lyapunov函数方法,设计基于观测器的控制器存在条件，并通过仿真实验证明提出方法的有效性。

1　问题描述

文献[5]中,给出两轮自平衡机器人系统状态方程,将针对该模型设计基于观测器的状态反馈控制器;

(1)

为处理该系统的状态估计问题,选取观测器的模型为:

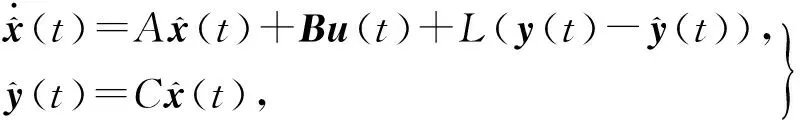
(2)

假定通过下述控制器来实现控制系统的设计

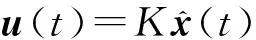
(3)

式(3)中,K为需要设计控制器增益。

(4)

文中的目的是设计控制器K和观测器L,使得闭环两轮自平衡机器人系统(4)能够稳定。

引理1[6]:对于任意矩阵X和负定矩阵Ω<0,存在常数α,使得不等式XΩXT<-α(X+XT)-α2Ω-1成立。

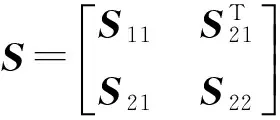
2　控制器设计

基于线性矩阵不等式方法,给出两轮自平衡机器人系统控制器及观测器的存在条件。

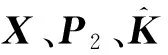
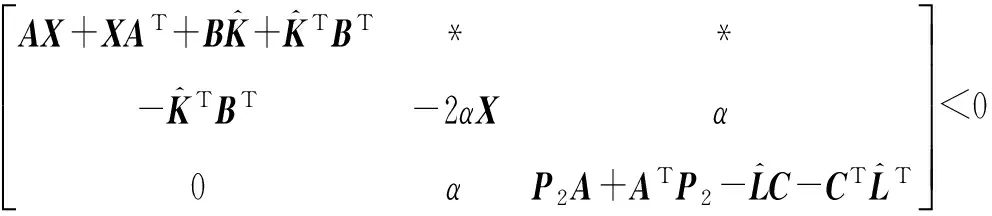
(5)

证明:定义如下Lyapunov函数

V(ψ(t))=ψT(t)Pψ(t),P>0,

(6)

对Lyapunov函数(6)求导，可得

(8)

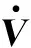
GTP+PG<0,

(9)

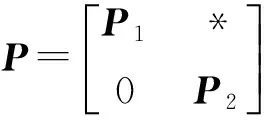
(10)

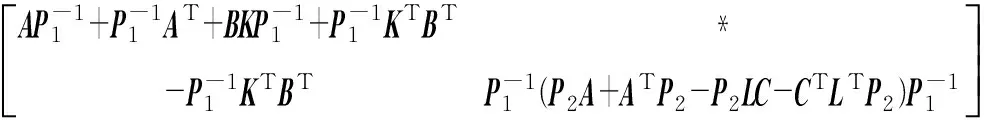
(11)

对不等式(11)运用引理1,可知存在常数α,使得不等式(12)成立:

(12)

对不等式(12)运用引理2,可得到

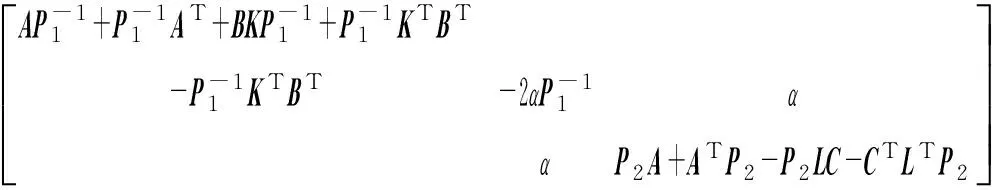
(13)

3　仿真实例

为证明提出方法的有效性,文献[5]中两轮自平衡机器人系统状态方程:

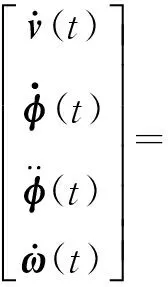
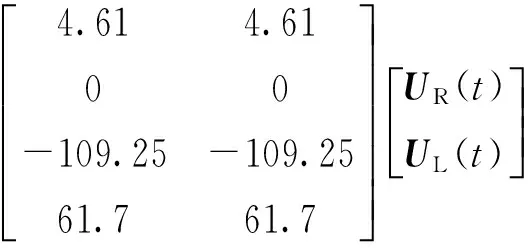
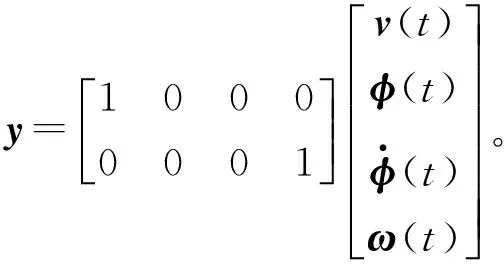
(14)

通过MATLAB LMI工具箱求解定理1中的矩阵不等式条件,求得控制器及观测器参数为:

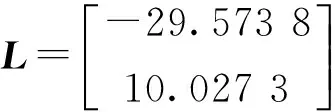
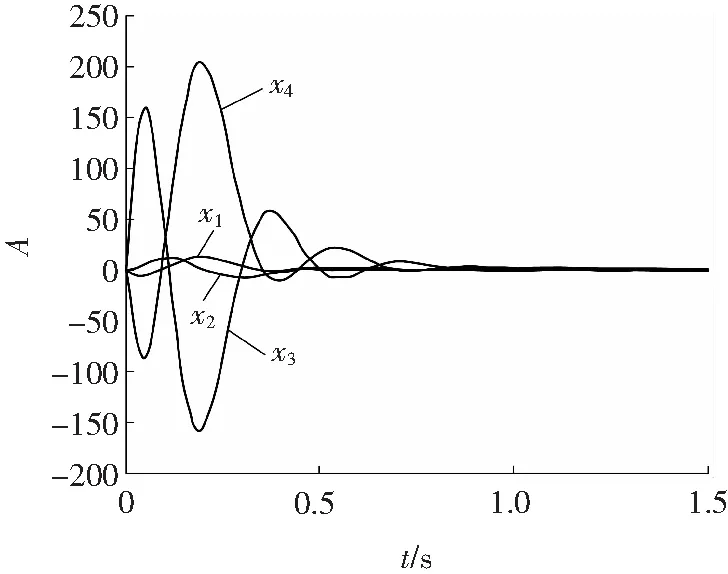
图1　系统状态响应曲线

4　结束语

两轮自平衡机器人系统,采用状态空间模型方法进行系统描述,并通过线性矩阵不等式(LMI)技术,利用Lyapunov函数方法,设计基于观测器的控制器存在条件,给出的矩阵不等式条件,可通过Matlab软件LMI工具箱求解出控制器及观测器增益。该方法通过仿真实验,证明了其方法的有效性。

[1]王瑜. 两轮自平衡机器人的控制技术研究[D]. 哈尔滨: 哈尔滨工程大学, 2009.

[2]王晓宇. 两轮自平衡机器人的研究[D]. 哈尔滨: 哈尔滨工业大学, 2007.

[3]阮晓钢, 任红格. 两轮自平衡机器人动力学建模及其平衡控制[J]. 计算机应用研究, 2009, 26(1): 99-101.

[4]陈伟, 延文杰, 周超英, 等. 两轮自平衡机器人控制系统的设计[J]. 传感器与微系统, 2008, 27(4): 117-120.

[5]李作庆. 两轮自平衡机器人控制系统研究与设计[D]. 哈尔滨: 哈尔滨工业大学, 2009.

[6]MANSOURI B, MANAMANNI N, GUELTON K, et al. Output feedback LMI tracking control conditions with H∞criterion for uncertain and disturbed T-S models[J]. Information Sciences, 2009, 179(4): 446-457.

[7]BOYD S, GHAOUI L E, FERON E, et al. Linear matrix inequalities in system and control theory[M]. Philadelphia: Society for Industrial and Applied Mathematics, 1994.

(编辑徐岩)

Design of two-wheeled self-balanced robot controller based on LMI

FANGHui

(College of Engineering, Bohai University, Jinzhou 121013, China)

This paper introduces a design of a controller based on linear matrix inequality (LMI) method to discuss the system of two-wheeled self-balanced robot. The design study is done by firstly is describing the system of two-wheeled self-balanced robot via state-space model; then using LMI method to design the controller and using Lyapunov function method to validate the method; and finally using the Matlab simulation experiment to prove the validity of the proposed method.

the system of two-wheeled self-balanced robot; LMI; Lyapunov function

2015-04-06

国家自然科学基金项目(61304149);辽宁省自然科学基金项目(2013020044)

方辉(1980-),男,辽宁省鞍山人，实验师，硕士,研究方向:非线性系统控制,E-mail:57527060@qq.com。

10.3969/j.issn.2095-7262.2015.03.021

TP242.6

2095-7262(2015)03-0340-03

A