关于粗理想和粗直积的一些性质定理*

2015-11-02黄卫华陆亚哲

重庆工商大学学报（自然科学版） 2015年7期

黄卫华，周平，陆亚哲

(文山学院数学学院，云南文山663000)

近年来，国内外学者将粗糙集思想引入代数系统，对粗糙群、粗糙半群、粗理想和粗直积等概念做了大量研究，得出了很好的结论［1－5］.文献［3］提出了半群中粗糙子半群和粗糙左(右、双侧、双)理想等概念;文献［5］定义了半群中的粗直积.此处讨论了粗理想和粗直积的关系，得到了一些较好的性质定理，进而丰富和完善了半群中的粗糙集理论.

1 预备知识

定义1［2］设S是一个半群，如果ρ是满足以下条件的S上的一个等价关系:对∀x∈S，(a，b)∈ρ⇒(ax，bx)∈ρ，(xa，xb)∈ρ，则称 ρ是 S 上的同余关系.记 x 所在的同余类为 [x]ρ={a∈S|(x，a)∈ρ}.

定义2［3］设A是S的任一子集，则A的ρ下近似和ρ上近似分别表示为

ρ(A)=(ρ－(A)，ρ－(A))称为 ρ粗糙集.

定义3［4］半群S上的一个同余关系ρ称为完备的，如果对∀a，b∈S，[a][b ]= [ a b].ρρρ

定义 4［4］设 ρ为半群 S 上的同余关系，ρ(A)，ρ－(A)，ρ(B)，ρ－(B)为 S 的非空粗子集，A，B⊆S，则 S－－上的粗直积记为

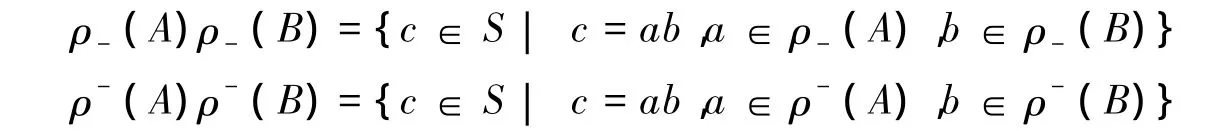
定义5 半群S的非空子集A称为S的子半群，如果AA⊆A.

定义6 半群S的非空子集A称为S的左(右)理想，如果SA⊆A(AS⊆A).

定义7 半群S的非空子集A称为S的(双侧)理想，如果SA⊆A且AS⊆A.

定义8 半群S的非空子集A称为S的双理想，如果ASA⊆A.

定义9 设ρ是半群S的一个同余关系，ρ－(A)≠∅，S的非空集A称为一个上(下)粗子半群，如果ρ－(A)(ρ－(A))是 S 的子半群，即 ρ－(A)ρ－(A)⊆ρ－(A)(ρ－(A)ρ－(A)⊆ρ－(A)).

定义10 设ρ是半群S的一个同余关系，ρ－(A)≠∅，S的非空集A称为一个上(下)粗左(右、双侧、双)理想，如果 ρ－(A)(ρ－(A))是 S 的左(右、双侧、双)理想，即

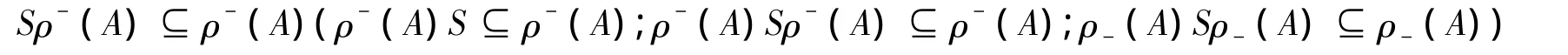
引理1 设A，B，C，D是半群S的非空子集，如果A⊆B，C⊆D，则AC⊆BD.

引理 2［4］设 ρ是半群 S 上的同余关系，A，B 是 S 的非空子集，则 ρ－(A)ρ－(B)⊆ρ－(AB)，ρ－(A)ρ－(B)⊆ρ－(AB).

引理 3［4］设 ρ，λ 是半群 S 上的同余关系，A，B∈S，则

(1)ρ－(A)⊆A⊆ρ－(A)，ρ－(S)=S= ρ－(S);

(2)ρ－(A∪B)= ρ－(A)∪ρ－(B)，ρ－(A∪B)= ρ－(A)∪ρ－(B);

(3)A⊆B⇒ρ－(A)⊆ρ－(B)，ρ－(A)⊆ρ－(B);

(4)ρ－(A)∪ρ－(B)⊆ρ－(A∪B)，ρ－(A∩B)⊆ρ－(A)∩ρ－(B).

2 主要结果

定理1 设A是半群S的一个左(右、双侧)理想，那么A是S的子半群.

证明因为A⊆S，A⊆A，由引理1知，AA⊆SA;又因为A是S的左理想，得SA⊆A，那么AA⊆SA⊆A，所以A是S的子半群.

其他情况可类似证明，略.

定理2 设ρ是半群S上的同余关系，如果A是S的一个子半群，则A是S的一个上粗子半群，即ρ－(A)是S的子半群.

证明由引理2知，ρ－(A)ρ－(A)⊆ρ－(AA)，已知 A是 S的一个子半群，则 AA⊆A，又由引理 3(3)知ρ－(AA)⊆ρ－(A)，所以 ρ－(A)ρ－(A)⊆ρ－(A).即 ρ－(A)是 S 的子半群，则 A 是 S 的一个上粗子半群.

推论1 设ρ是半群S上的同余关系，如果A是半群S的一个左(右、双侧)理想，则A是S的一个上粗子半群.

证明由定理1和定理2直接推知.

定理3 设ρ是半群S上的同余关系，如果A是S的一个右(左、双侧、双)理想，则A是S的一个上粗右(左、双侧、双)理想.

证明设A是S的一个右理想，即AS⊆A，由引理3(3)知，ρ－(AS)⊆ρ－(A)，又由引理3(1)知 ρ－(S)=S，于是有 ρ－(A)S= ρ－(A)ρ－(S)，又由引理 2 知，ρ－(A)ρ－(S)= ρ－(AS)，所以 ρ－(A)S⊆ρ－(AS)⊆ρ－(A)，即ρ－(A)是S的右理想，故A是S的一个上粗右理想.

其余情况的证明类似.

以上两个定理说明上粗子半群(左理想、右理想、双侧理想)是通常的子半群(左理想、右理想、双侧理想)等概念的扩张，下面的例子说明定理3的逆不成立.

例1 设S={a，b，c，d}是一个半群，其上的运算由表1定义，S上的同余关系ρ所决定的同余类为{a}，{d}，{b，c}，设 A={b}，则 ρ－(A)={b，c}，且 ρ－(A)S={b，c}S=S{b，c}=Sρ－(A)= ρ－(A).故 A 是一个上粗双侧理想，但是SA={b，c}⊄A，故A不是S的双侧理想.

表1 S上的运算

定理4 设ρ是半群S上的完备同余关系，ρ－(A)≠∅，如果A是S的一个子半群，则A是S的一个下粗子半群，即ρ－(A)是S的子半群.

证明已知A是S的一个子半群，则AA⊆A，由引理3(1)知，ρ－(A)⊆A⊆S，又因为ρ是半群S上的完备同余关系，则有 ρ－(A)ρ－(A)⊆ρ－(AA)⊆ρ－(A)，即 A 是 S 的一个下粗子半群，则 ρ－(A)是 S 的子半群.

推论2 设ρ是半群S上的完备同余关系，ρ－(A)≠∅，如果A是半群S的一个左(右、双侧)理想，则A是S的一个下粗子半群.

证明由定理1和定理4直接推知.

定理5 设ρ是半群S上的一个完备同余关系，如果A是S的一个右(左、双侧、双)理想，且ρ－(A)≠∅，则ρ－(A)是 S的一个右(左、双侧、双)理想.

证明设 A 是 S的一个右理想，即 AS⊆A，由引理3(3)知，ρ－(AS)⊆ρ－(A)，又由引理 3(1)知，ρ－(S)=S，于是有 ρ－(A)S=ρ－(A)ρ－(S)，又由引理 2 知，ρ－(A)ρ－(S)= ρ－(AS)，所以 ρ－(A)S⊆ρ－(AS)⊆ρ－(A)，即ρ－(A)是S的右理想，故A是S的一个下粗右理想.

其余情况的证明类似.

定理6 设ρ是半群S上的同余关系，如果A，B分别是S的右理想和左理想，则

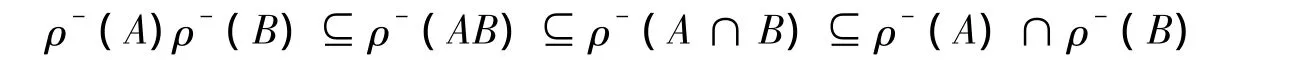
证明因为 ρ是半群 S 上的同余关系，由引理 2 知，ρ－(A)ρ－(B)⊆ρ－(AB).下证 ρ－(AB)⊆ρ－(A∩B).由引理1知，AB⊆AS，又因为A是S的一个右理想，则AS⊆A，所以AB⊆A，同理AB⊆B，故AB⊆A∩B.由引理3(3)知，ρ－(AB)⊆ρ－(A∩B)，由引理 3(4)得，ρ－(A∩B)⊆ρ－(A)∩ρ－(B)，故 ρ－(A)ρ－(B)⊆ρ－(AB)⊆ρ－(A∩B)⊆ρ－(A)∩ρ－(B).

定理7 设ρ是半群S上的一个完备同余关系，且ρ－(A)≠∅，如果A，B分别是S的右理想和左理想，则