二元域上一类正规基与q-循环*

李 波

(重庆邮电大学移通学院，重庆401520)

1 基础知识

设q为素数p的方幂，n(≥2)为正整数，Fqn是 q元域 Fq的 n(≥2)次扩张.若 N={αi=αqi|i=0，1，…，n－1}是Fqn到Fq的一个正规基，则称α是Fqn到Fq的一个正规元.设

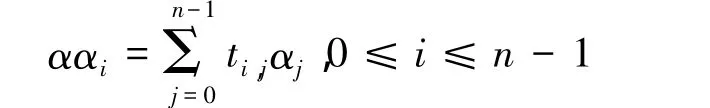
则(ti，j)n×n中非零元的个数称为 N 的复杂度，记为 CN.R Mullin 等［1］证明了 CN≥2n－1，当 CN=2n－1 时，称 N为最优正规基.以最优正规基为代表的低复杂度正规基已经有许多结果［2－11］.R Mullin等给出了Ⅰ型和Ⅱ型最优正规基的构造定理之后;高绪洪［12］证明了只存在这两类最优正规基;1990年，A Wassermann［13］把最优正规基推广为k－型高斯正规基.

定义1［13］设q为素数p的方幂，k和n为正整数，且满足 kn+1为素数，(kn+1，p)=1.假定 γ∈Fqkn是kn+1次本原单位根，s是q模kn+1的次数.若(kn/s，n)=1，l是Zkn+1的一个k本原的单位根，则

生成Fqn到Fq的一个正规基，称N为Fqn到Fq的一个k－型高斯正规基.

注1 设N为Fqn到Fq的一个k－型高斯正规基，由Ⅰ型和Ⅱ型最优正规基的定义可知，当k=1时，N为Ⅰ型最优正规基;当k=q=2时，N为Ⅱ型最优正规基.

熟知，最优正规基(特别是低复杂度正规基)在编码理论、密码学、数字通信等领域有着广泛的应用.通过计算发现，当扩张次数 n=4，8，16 时，存在 F2n到 F2的正规基 N，使得序列 ti=Tr(ααi)(i=0，1，…，n－1)中t0=t1=tn－1=1，ti=0(i≠0，1，n－1)，其中 Tr表示 Fqn到 Fq的迹映射.这类正规基在编码中有着很好的应用.自然的问题是:扩张次数 n满足什么条件，才存在 F2n到 F2的正规基满足 t0=t1=tn－1=1，ti=0(i≠0，1，n－1).

由有限域上正规基的性质可知，ti=tn－i.Perlis［14］给出了如下结论:设 q=ps，p 为素数，n=pm，m≥1.若 α∈Fqn，则 α 为 Fqn到 Fq的一个正规元⇔Tr(α)≠0.从而当 n=2t(t≥1)时，t0=1.故此时只需考虑 i≠0 的情形.对于k－型高斯正规基，文献［7］得到了如下结论:若α生成Fqn到Fq的一个k－型高斯正规基，则Tr(α)=－1.

下面给出q－循环的定义.

定义 2［15］设 a0，a1，…，al－1为{0，1，…，m－1}中 l个不同的元素，q 为素数的方幂，若满足

则称序列(a0，a1，…，al－1)为一个模 m 的 q－循环，l为该 q－循环的长度.

以下用 li表示 i模 qn－1 的 q－循环的长度.由定义 2，iqli≡i(mod qn－1).

2 主要结果及证明

这里先给出一个引理.

引理 1［12］设 k，n 是正整数，kn+1 为素数，q 模 kn+1 的阶是 e.如果(kn/e，n)=1，T 是 Zkn+1的一个 k－次本原单位根，则Zkn+1中任意非零元r都能唯一表示成如下形式:

定理1 设q为素数的方幂，n(≥2)是正整数，则li|n，其中0≤i≤qn－1.

证明 由文献［15］知若ξ是Fqn的一个本原元，且存在k个不同的q－循环，令i1，i2，…，ik分别来自这k个不同的q－循环，则xn－1在Fq上的完全分解式为

形如 Fe=22e+1(e≥0)的数被称为费马数.对于任意给定的两个费马数 Fe1，Fe2;若 e1≠e2，则(Fe1，Fe2)=1.下面运用这个性质给出一种特殊情形下2i+1模2n－1的2－循环的长度的计算公式.

证明 易知，2n－1=22t－1=Ft－1Ft－2…F0，2i+1=Fm.令 2l2i+1－1=Ft－1Ft－2…F0.由定理 1，l2i+1|n，则 t1－1≤t－1，即 t1≤t.又 2i+1≡(2i+1)2l2i+1(mod(2n－1))，即 2n－1|(2i+1)(2l2i+1－1).于是

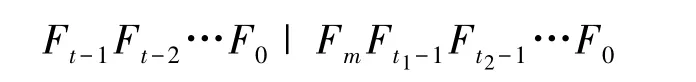
由于不同的费马数必定互素，则 t－2≤t1－1，即 t－1≤t1.从而，t－1≤t1≤t.当 t1=t时，m≠t－1，此时 l2i+1=n;当t=t－1 时，m=t－1，此时

例1 条件同推论2，

当 i=1 时，m=0，有若 t≥2，则 m＜t－1，此时 l=n;若 t=1，则 m=t－1，此时

当 i=2 时，m=1，有若 t≠2，则 m≠t－1，此时 l=n;若 t=2，则 m=t－1，此时

关于是否存在 F2n到 F2的正规基满足 t0=t1=tn－1=1，ti=0(i≠0，1，n－1)，有

定理2 设 N={αi|i=0，1，…，n－1}是 F2n到 F2上的一个 k－型高斯正规基，则

1)若 k为偶数，或 k为奇数且 n≠4，则 N 不满足 t0=t1=tn－1=1，ti=0(i≠0，1，n－1);

由定义1知，当n=4时，不存在F2n到F2上的Ⅱ型最优正规基.

注 2 通过定义可以验证，当 n=4 时，F2n到 F2上的Ⅰ型最优正规基满足 t0=t1=tn－1=1，ti=0(i≠0，1，n－1).

由定理2和注1，注2，有

推论 3 设 N={αi|i=0，1，…，n－1}是 F2n到 F2上的一个正规基，且满足 t0=t1=tn－1=1，ti=0(i≠0，1，n－1)，则

1)当n=4时，N可为Ⅰ型最优正规基;

2)当n≠4时，N一定不是最优正规基.

［1］MNLLIN R，ONYSZCHUK I，VANSTONE S，et al.Optimal Normal Bases Over Fpn［J］.Discrete Applied Math，1999(22):149-161

［2］LIAO Q Y，SUN Q.Normal Bases and Their Dual-bases Over Finite Fields［J］.Acta Mathematics Sinica，2006，22(3):845-848

［3］LIAO Q Y.On the Distribution of Normal Bases Over Finite Fields［J］.Advances in Mathmatics，2010，39(2):207-211

［4］廖群英，孙琦.有限域上最优正规基的乘法表［J］.数学学报，2005，48(5):947-954

［5］WAN Z X，ZHOU K.On the Complexity of the Dual Bases of a Type I Optimal Normal Bases［J］.Finite Fields and Their Applications，2007，13(4):411-417

［6］GAO SH.Abelian Groups，Gauss Periods，and Normal Bases［J］.Finite Fields and Their Applications，2001，7(1):149-161

［7］廖群英，苏丹丹，付萍.有限域上的2型高斯正规基及其对偶基［J］.四川大学学报:自然科学版，2010，47(6):1221-1224

［8］ASH D，BLAKE I F，VANSTONE S.Low Complexity Normal Bases［J］.Discrete Applied Math，1999(25):191-210

［9］NOGAMI Y，NASU H，MORIKAWA Y，et al.A Method of Constructing a Self-dual Normal Bases in Odd Characteristic Extention Fields［J］.Finite Fields and Their Applications，2008，14(2):867-876

［10］李俊，黄琴，李波，等.有限域上的k-型高斯正规基及其对偶基［J］.四川师范大学学报:自然科学版，2011，34(3)，289-295

［11］YOUNG B，PANARIO D.Low Complexity Normal Bases［J］.Finite Fields and Their Applications，2004，10(1):53-64

［12］GAO SH.Normal Bases Over Finite Fields［D］.Waterloo:Waterloo University，1993

［13］WASSERMANN A.Konstruktion Von Normalbasen［J］.Bayreuther Mathmatische Schriften，1990(31):155-164

［14］PERLISS.Normal Bases of Cyclic Fields of Prime Power Degree［J］.Duke Math，1942(9):507-519

［15］WAN Z X.Lectures on Finite Fields and Galois Rings［M］.Singapore:World Science Publishers，2003

［16］李波，廖群英.有限域上k-型高斯正规基的对偶基及其乘法表［J］.四川师范大学学报:自然科学版，2013，36(6):824-829