基于ARX参数模型的某型抗荷调压器系统辨识

经验人：王 鹏 杨晓萍 曹煜国

基于ARX参数模型的某型抗荷调压器系统辨识

经验人：王 鹏 杨晓萍 曹煜国

本文对系统辨识基本原理进行了简要介绍，利用Matlab系统辨识工具箱，完成了某型抗荷调压器的系统辨识与ARX（扩展自回归模型）参数模型建立，其预测结果具有较高准确性。此方法对于在试飞阶段缺少被试产品技术资料情况下，了解掌握系统输入输出特性具有较好作用。

抗荷调压器是飞机抗荷系统的主要组成部分。调压器根据飞机过载大小，将来自环控系统的引气调节至合适的压力范围内，以供给飞行员抗荷装具使用，其作用是减轻过载对人体机能的不良影响，提高飞行员抗过载能力，从而最大程度地发挥飞机的机动性。

对于抗荷系统飞行试验来说，课题人员往往由于种种客观原因，不能获得被试产品详细技术资料，导致需要用较多飞行架次评估系统性能，严重时会影响到型号试飞进度。

笔者通过学习相关系统辨识资料，结合日常使用Matlab经验，以某型抗荷调压器为对象，采用ARX参数模型完成了系统辨识，建立的系统模型能够以飞机过载作为输入条件，预测抗荷调压器输出压力，预测精度能够满足系统评估需要。

系统辨识原理及方法

系统辨识原理

基于试验数据及试验过程的系统建模过程，通常称为“系统辨识”，其实质是从输入输出数据中提取被研究对象的数学模型，它是系统建模的一个十分重要的途径。

随着现代控制理论的迅速发展，过程控制及计算机技术的不断进步，“系统辨识”已经成为在理论和方法上都有着鲜明特色的学科，广泛而有效地应用于航空航天领域。

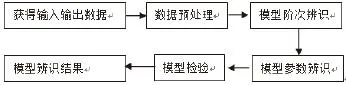
图1　系统辨识流程图

系统辨识的一般流程如图1所示。

系统辨识方法

常用的系统辨识方法有：

非参数模型辨识方法

它是在假定系统是线性的条件下，不必事先确定模型的具体结构。主要有阶跃响应法、脉冲响应法、频率响应法、相关分析法、谱分析法等。

参数模型辨识方法

此方法必须假定一种模型，通过极小化模型与系统间的误差准则来确定模型的参数。主要有最小二乘法、极大似然法、贝叶斯估计法、线性最小方差估计、神经网络方法等。

其中最小二乘法因其结构简单、收敛速度快、辨识精度较高、性能可靠、对先验数据依赖低、且在工程上易于实现等众多优点，因此受到工程人员和科研人员的重视，应用极为广泛。

结合实际工作，本文选用参数模型辨识方法。

参数模型选取

就工程实际而言，一般化随机模型为：

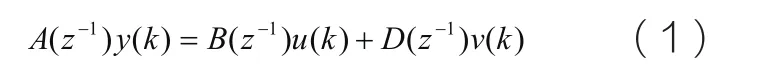
由此模型可提供以下模型：

（1） ARMAX模型（扩展自回归滑动平均模型）

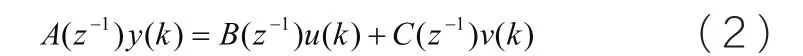
（2） ARX模型（扩展自回归模型）

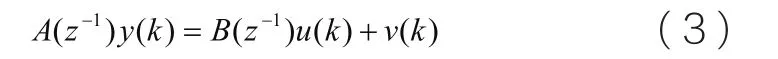
（3）Box-Jenkins模型（输出误差模型）

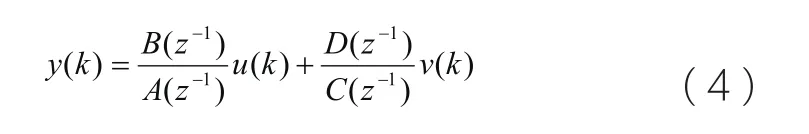
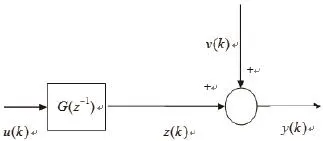
图2　ARX模型结构示意图

系统辨识时模型类的选择要秉承最小化原理，尽量用最可能少的参数来表示要辨识的系统。因此，模型类的选用需要统筹考虑，兼顾多种因素。

本课题应用以上方法对实测数据进行辨识对比分析，其中ARX模型辨识结果拟合度较高。因此本文将重点说明某型抗荷调压器ARX参数模型辨识的实现。

ARX模型结构如图2所示。

图中，输入u（k）和输出y（k）都是可以观测的；G（z-1）是系统模型，用来描述系统的输入出输出特性；v（k）是白噪声。

系统的描述方程为：

式中：y（k）为系统输出量的第k 次观测值，y（k-1）为系统输出量的第（k-1）次观测值，后面依次类推；u（k）为系统的第k 次输入值，u（k-1）为系统的第（k-1）次输入值，依此类推；将（5）式改写为：

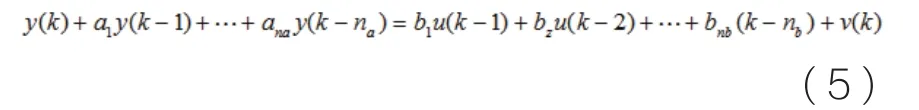
可得系统输入输出的最小二乘格式为：

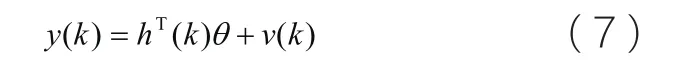
式中：h 为样本集合；θ为被辨识的参数集合。

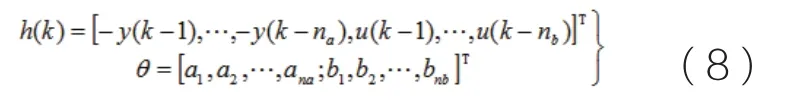
取准则函数

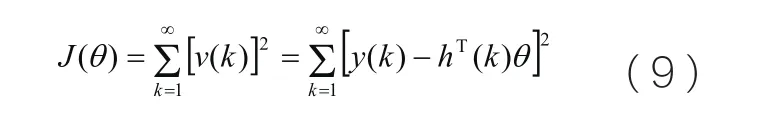
通过式（9）可以看出，未知模型参数θ最可能的值是在实际观测值与计算值之累积误差的平方和达到最小值处，所得到的这种模型输出能够最接近实际系统的输出。使得J（θ）为最小值时θ估计值记作称为参数θ的最小二乘估计值。求得的必要条件为：

某型抗荷调压器ARX参数模型的Matlab实现

Matlab系统辨识工具箱包括了ARX模型、ARMAX模型、Box-Jenkins模型和状态空间模型等。表1列举了Matlab中常见的参数模型辨识函数。

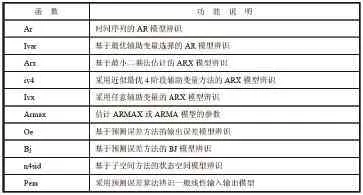
表1　参数模型辨识函数

输入输出数据获取及预处理

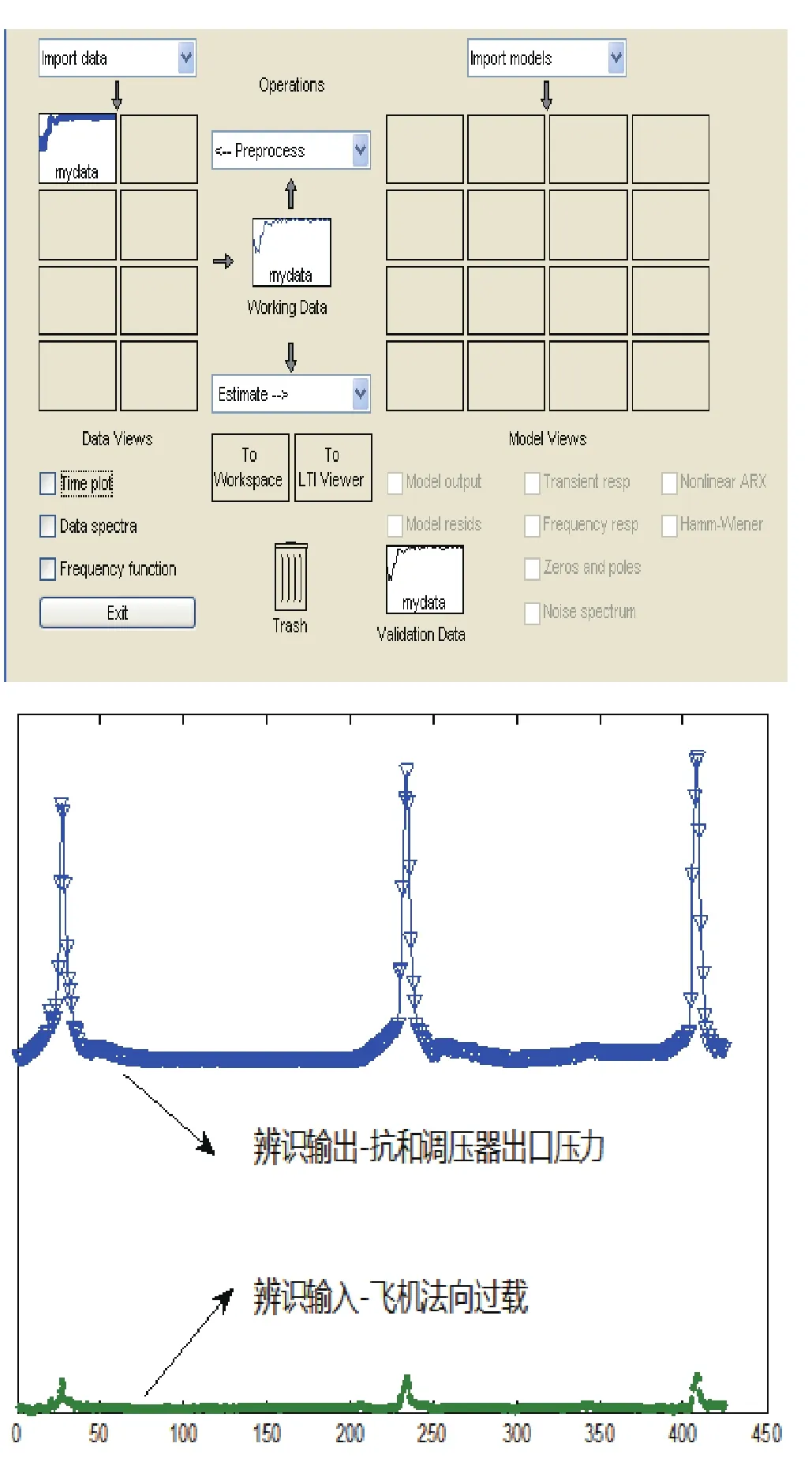
图3　输入输出数据导入及预处理结果

对于某型抗荷调压器来说，将飞机过载值作为输入（x1），抗荷调压器出口压力作为输出（y1），导入Workspace，用绘图指令（plot）将数据画成曲线， 观察了解系统的时域或频域特性。对输入输出数据要进行异常值剔除、数据有效性检验、数据类型和结构转换等预处理。利用iddata命令生成标准包含输入输出数据的对象。如图3所示。

模型定阶

Matlab辨识工具箱已提供了方便、直观的模型阶次选择工具。模型的辨识算法已封装到ARX函数中。系统辨识工具箱可以生成以下多种类型的模型：频率响应模型、冲击响应模型、低阶传输函数（过程模型） 、输入输出多项式模型、状态空间方程模型、非线性（黑箱）模型、常微分或差分方程（灰箱）模型。

调用Matlab中计算多个单ARX模型损失函数的函数为arxstruc和模型结构选择函数为selstruc，它可以计算和比较ARX模型的损失函数值，并得到最小损失函数所对应的阶次（图4中红圈显示）。

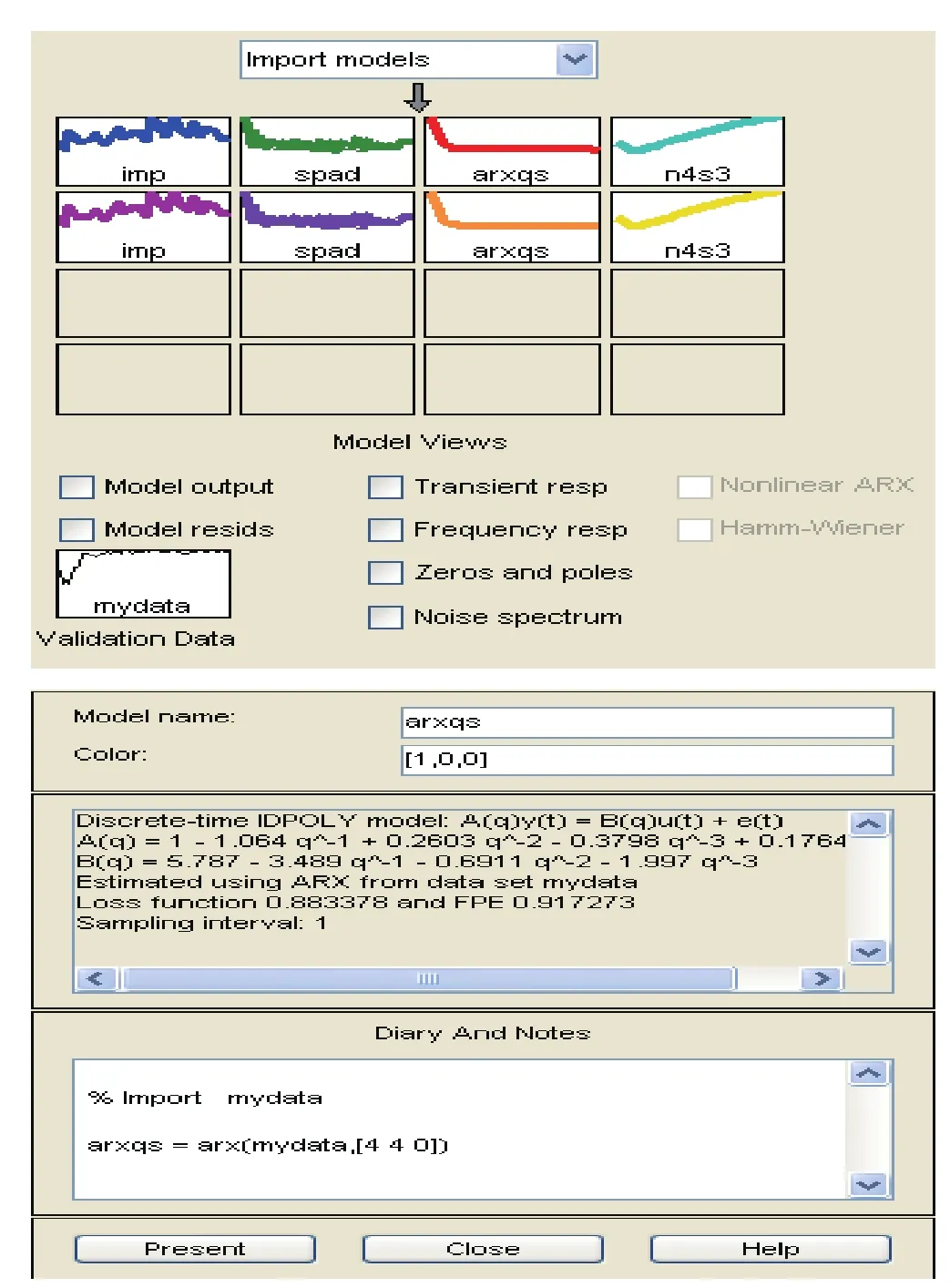
图4　模型定阶结果

传递函数获取

通过上述模型定阶可以得出系统离散模型的系数，调用Matlab中的d2c函数，可以将上文辨识得出的离散模型转换为控制系统传递函数模型。

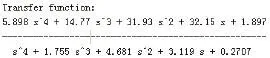
系统模型检验

将试验数据中的输入（飞机法向过载数据）作为辨识得到的ARX模型的输入，获得仿真输出，与实测输出（抗荷调压器出口压力）进行对比，计算拟合度。图5是采用辨识得到的模型预测的抗荷调压器出口压力，可以看出模型拟合度较高，达到了89％（图5中红圈）。

图6是残差互相关性分析。结果显示：残差在合理的公差带以内，即模型参数在置信区间内，模型有效。

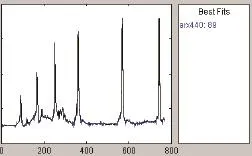
图5　辨识模型预测数据与实测数据对比（拟合度89％）

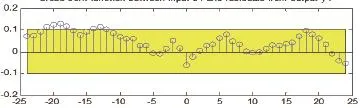
图6　残差互相关分析

结束语

系统辨识方法在机理尚不清楚或机理过于复杂的系统动态特性研究中具有广泛应用；

本文建立的某型抗荷调压器ARX参数模型与文献中抗荷调压器模型在结构上具有一致性，从而验证了系统辨识的准确性；

建立的系统模型能够以飞机过载作为输入条件，预测抗荷调压器输出压力，预测精度能够满足系统评估需要，其结果具有代表性；

Matlab系统辨识工具箱具有强大的运算和分析功能，利用其进行系统辨识，可以大大提高辨识的速度和精度，并且辨识结果直观，准确度高。

10.3969/j.issn.1001-8972.2015.10.043