五轴数控机床精度建模与预测研究*
2015-11-02关立文王立平
黄 克,关立文,王立平
(1.电子科技大学机械电子工程学院,成都 611731;2.清华大学机械工程系,北京 100084)
五轴数控机床精度建模与预测研究*
黄 克1,关立文2,王立平2
(1.电子科技大学机械电子工程学院,成都 611731;2.清华大学机械工程系,北京 100084)
零部件几何误差导致的机床空间误差是影响数控机床加工精度的主要原因,为了明确机床运行过程中各单元几何误差对加工精度的影响程度及规律,从而经济合理地分配机床零部件的几何精度,基于多体系统理论建立了五轴数控机床的精度预测模型。利用精度模型进行了加工精度预测的单因素对比实验分析,选取NAS979圆锥台试件圆度误差作为分析对象,改变机床的部分几何误差参数值,得到参数改变对NAS979圆锥台试件圆度误差产生的影响及特点,即各零部件几何误差对加工精度的影响分布规律,为机床设计方案的改进及精度分配提供了理论参考。
五轴数控机床;几何误差;精度建模;精度预测
0 引言
五轴数控机床以柔性好、加工精度高、自动化程度高等优点在现代制造业中已得到广泛应用,并在迅速发展和普及。数控机床加工的目标是生产出高精度的产品,在设计、使用和误差补偿过程中,都需要准确把握数控机床的误差。为了明确机床运行过程中各单元误差对加工精度的影响程度,进行数控机床加工精度预测研究工作是十分必要的。对于数控机床特别是多轴联动数控机床,在实际加工之前,更需要进行加工精度预测,以便指导生产实践。因此研究数控机床加工精度预测既有重要的理论意义,又有很好的应用价值[1]。
数控机床的综合几何误差体现在机床各零部件上,最终将反映在被加工工件的加工精度上。而通过准确建立数控机床的精度模型,可以反映出机床整体精度与各零部件的精度关系。国内外许多学者对数控机床空间误差建模方法进行了较广泛而深入的研究,先后出现了几何建模法、误差矩阵法、二次关系模型法、机构学建模法、刚体运动学法和多体系统理论法等[2-6]。在众多研究中,对多体系统理论建模方法研究较多,但利用这种方法建立的模型对机床进行精度预测与精度规律分析却很少。
本文在国家科技重大专项“五轴联动数控机床精度测评技术与标准”的课题背景下,对五轴数控机床进行研究。利用多体系统理论分析各部件几何误差对机床加工精度的影响,建立了机床的精度模型,并利用精度模型进行了加工精度预测的单因素对比实验分析,得到各零部件几何误差对加工精度的影响分布规律,为经济合理地分配机床零部件的几何精度提供理论参考。
1 NAS979检测试件简介
美国国家航空航天局(NASA)于1969年制定了“通用切削测试——NAS系列金属切削装备规范”,该规范共包含了两个试件,如图1所示。其中图1a试件主要用于检测三轴机床平动轴的几何精度和位置精度;图1b试件又名NAS979圆锥台试件,主要用于多轴联动机床转动轴精度检测,该试件由一个圆锥台和方形基座组成,其中,圆锥台与水平面成15°夹角。NAS979圆锥台试件是目前应用最广泛的五轴数控机床精度检测试件[7]。

图1 NAS979系列试件
2 基于多体系统理论的精度建模
选定沈阳机床集团生产的某型号五轴数控机床作为研究对象,根据其结构与运动特点,将机床抽象成多体系统,用齐次特征矩阵把机床各部件的误差量之间的耦合关系表述出来;推导出机床中两相邻体之间相对运动的特征矩阵和运动方程,从而建立五轴数控机床的精度模型。
2.1五轴数控机床特征矩阵的求解
本文所研究的AB型五轴数控机床的结构示意图如图2所示。

图2 五轴数控机床结构示意图
该五轴机床的结构有两个分支,分别为床身到工件的分支(0→1→2)和床身到刀具的分支(0→3→4→5→6→7→8)。
一般来说,机床的每个单元在处于静止或运动状态时都存在空间6个自由度方向的基本误差,通过分析五轴机床的结构及其运动关系可知,影响机床加工精度的几何误差主要有33项,这部分几何误差在机床总误差中占了较大比重[8-11]。下面将对各误差项进行分析:对于移动轴来讲,以X轴为例,当沿X轴移动时,存在定位误差δx(X)、Y方向直线度误差δy(X)、Z方向直线度误差δz(X),以及滚转误差εx(X)、偏摆误差εy(X)和俯仰误差εz(X);同理,对于Y轴,存在δy(Y)、δx(Y)、δz(Y)、εx(Y)、εy(Y)、εz(Y)六项误差;对于Z轴,存在δz(Z)、δx(Z)、δy(Z)、εx(Z)、εy(Z)、εz(Z)六项误差;对于转动轴来讲,以A轴为例,当A轴转动时,共存在六项误差,包括三项平动误差δx(A)、δy(A)、δz(A)和三项转动误差εx(A)、εy(A)、εz(A);同理,对于B轴,共存在δy(B)、δx(B)、δz(B)、εx(B)、εy(B)、εz(B)六项误差;另外还有三项垂直度误差Sxy、Syz、Szx。
根据该数控机床的结构和各部件之间的运动关系,可建立各相邻体间的变换特征矩阵。对于任意两个坐标系Oi-xiyizi和Oj-xjyjzj,用矩阵jTip和jTis分别表示描述空间点在各坐标系中的静止位置坐标变换和运动位置坐标变换。由于篇幅限制,仅列出部分特征矩阵:

多体系统中的任何一个高序体j,其最终的位置和姿态都可以由低序列体i通过一系列的变换得到[12]。多体系统的体间实际特征矩阵为:

2.2机床精度模型
给每一个机床结构部件和圆锥台试件建立右旋正交笛卡尔坐标系Oi-xiyizi(i=0,1,2,……,n)。设刀具成形点P在刀具坐标系中的齐次坐标为:

刀具成形点在NAS979坐标系内的理想成形函数为:
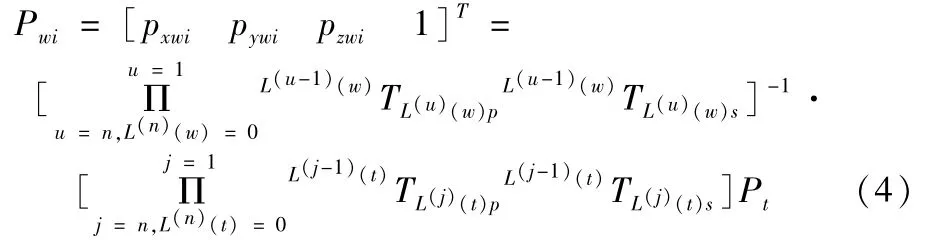
当机床作实际成形运动时,点P在NAS979试件坐标系中的齐次坐标形式为:

刀具成形点在NAS979试件坐标系内的实际成形函数为:

在机械加工中,机床加工精度最终是由机床上刀具成形点与工件成形点之间的相对位移误差决定的。在实际加工过程中,刀具成型点的实际位置不可避免地会偏离理想位置,从而产生空间位置误差,该AB型五轴数控机床的精度模型为:

3 机床加工精度预测的对比实验分析
(1)Y、Z、A、B轴的各项几何误差、垂直度误差值不变,只改变X轴的定位误差(每次实验X轴的定位误差的取值依次为:0.025、0.020、0.015、0.010、0.005),实验结果如图3所示。

图3 X轴定位误差变化对试件圆度误差的影响
仿真结果表明,当其他各项几何误差不变,X轴的定位误差在区间(0.005,0.015)/mm内,NAS979圆锥台试件圆度误差随着X轴的定位误差的增大而减小,可能是因为误差耦合造成的;X轴的定位误差在区间(0.015,0.020)/mm内变化,对NAS979圆锥台试件圆度误差的影响基本不变;X轴的定位误差在区间(0.020,0.025)/mm内,NAS979圆锥台试件圆度误差随着X轴定位误差的增大而增大。从图中也可看出,试件在部分区域对误差变化比较敏感,在不同的敏感区域,敏感程度也不一样。
(2)X、Y、Z、A、B轴的各项几何误差值不变,只改变垂直度误差(每次实验垂直度误差取值依次为:0.004、0.003、0.002、0.001、0.0005),实验结果如图4所示。

图4 垂直度误差变化对试件圆度误差的影响
仿真结果表明,当其他各项几何误差不变,垂直度误差在区间(0.0005,0.004)/mm内,NAS979圆锥台试件圆度误差随着垂直度误差的增大而增大。因此,垂直度误差的变化对试件圆度误差的影响比较大,或者说试件对垂直度误差比较敏感。
(3)X、Z、A、B轴的各项几何误差、垂直度误差值不变,只改变Y轴的定位误差(每次实验Y轴的定位误差取值依次为:0.006、0.005、0.004、0.003、0.002),实验结果如图5所示。

图5 Y轴定位误差变化对试件圆度误差的影响
仿真结果表明,当其他各项几何误差不变,Y轴的定位误差在区间(0.003,0.006)/mm内,NAS979圆锥台试件圆度误差随着Y轴定位误差的增大而增大;Y轴的定位误差在区间(0.002,0.003)/mm内,随定位误差的变化,圆度误差的幅度变化不是很明显。
(4)X、Y、Z、B轴的各项几何误差、垂直度误差值不变,只改变A轴的绕自身转角误差(每次实验A轴绕自身转角误差取值依次为:0.0030、0.0025、0.0015、0.0010、0.0005),实验结果如图6所示。

图6 A轴绕自身转角误差变化对试件圆度误差的影响
仿真结果表明,当其他各项几何误差不变,A轴的绕自身转角误差在区间(0.0005,0.0015)内,随着A轴角度误差的变化,圆度误差的幅度变化不明显;A轴的绕自身转角误差在区间(0.0015,0.0030)内,NAS979圆锥台试件圆度误差随着A轴角度误差的增大而增大。从图中也可看出,试件在部分区域对误差变化比较敏感,在不同的敏感区域,敏感程度也不一样。
5 结论
数控机床的精度建模是机床精度设计的关键技术,也是保证机床加工精度的重要环节。利用多体系统理论,综合考虑了机床的各零部件之间的几何误差,对AB型五轴数控机床建立了精度模型。该建模方法简便、明确,将整体与部分的关系有机耦合,为实现精度分配提供了理论基础。
利用精度模型进行了加工精度预测的单因素对比实验分析,选取NAS979圆锥台试件圆度误差作为分析对象,改变机床的部分几何误差参数值,得到参数改变对NAS979圆锥台试件圆度误差产生的影响及特点,即各零部件几何误差对加工精度的影响分布规律,为经济合理地分配机床零部件的几何精度提供理论参考。
[1]粟时平.多轴数控机床精度建模与误差补偿方法研究[D].长沙:国防科学技术大学,2002.
[2]任永强,杨建国,窦小龙,等.五轴数控机床综合误差建模分析[J].上海交通大学学报,2003,37(1):70-75.
[3]粟时平,李圣怡.五轴数控机床综合空间误差的多体系统运动学建模[J].组合机床与自动化加工技术,2003(5):15-21.
[4]Jung JH,Choi JP,Lee S J.Machining accuracy enhancement by compensating for volumetric errors of a machine tool and on-machine measurement[J].Journal of Materials Processing Technology,2006,174:56-66.
[5]Kong L B,Cheung C F,TO S,etal.A kinematics and experimental analysis of form error compensation in ultra-precision machining[J].International Journal of Machine Tools& Manufacture,2008,48;1408-1419.
[6]刘丽冰,王广彦,刘又午.复杂机械系统运动误差自动建模技术研究[J].中国机械工程,2000,11(6):642-646.
[7]霍彦波,丁杰雄,谢东,等.五轴数控机床转动轴与平动轴联动的轮廓误差仿真分析[J].组合机床与自动化加工技术,2012(3):21-25.
[8]Jha B K,Kumar A.Analysis of geometric errors associated with five-axis machining centre in improving the quality of cam profile[J].International Journal of Machine Tools& Manufacture,2003,43:627-636.
[9]Okafor A C,Ertekin Y M.Derivation of machine tool error models and error compensation procedure for three axes vertical machining center using rigid body kinematics[J].International Journal of Machine Tools&Manufacture,2000,40:1199-1213.
[10]Du ZC,Zhang SJ,Hong M S.Development of a multi-step measuring method for motion accuracy of NC machine tools based on cross grid encoder[J].International Journal of Machine Tools&Manufacture,2010,50(3):270-280.
[11]Pott A,Kecskemethy A,Hiller M.A simplified force-based method for the linearization and sensitivity analysis of complex manipulation systems[J].Mechanism and Machine Theory,2007(42):1445-1461.
[12]赵小松,刘丽冰,章青,等.四轴联动加工中心误差模型及参数辨识[J].机械工程学报,2000(6):63-76.
(编辑 赵蓉)
Study on Precision Modeling and Prediction of Five-axis NC Machine Tool
HUANG Ke1,GUAN Li-wen2,WANG Li-ping2
(1.School of Mechatronics Engineering,University of Electronic Science and Technology,Chengdu 611731,China;2.Department of Mechanical Engineering,Tsinghua University,Beijing 100084,China)
The volumetric error resulted from geometric errors of parts is the main reason affecting the machining accuracy.In order to determine the influence rule on the processing precision generated by the geometric errors of parts,thus distribute the geometric errors of parts economically and reasonably.Based on the theory of multi-body system,the precision prediction model of five-axis vertical machining center was established.Analysis of univariate comparative experiments of machining precision prediction were carried out by using the precision prediction model.The contour error of NAS979 specimen was analyzed.The result indicate the influence rule of the processing precision generated by the geometric errors of parts,the work provide a basis for the improvement of the machine tool design concept and the precision deployment. Key words:five-axis NC machine tool;geometric error;precision modeling;accuracy prediction
TH166;TG659
A
1001-2265(2015)02-0078-04 DOI:10.13462/j.cnki.mmtamt.2015.02.022
2014-06-15;
2015-01-07
高档数控机床与基础制造装备科技重大专项(2014ZX04014-031)
黄克(1989—),男,银川人,电子科技大学硕士研究生,研究方向为数控机床精度检测,(E-mail)thuhuangk2013@126.com。
