基于S曲线加减速的NURBS插补控制方法研究*
2015-11-02赵国勇刘晨希安红静
岳 磊,赵国勇,刘晨希,安红静
(山东理工大学机械工程学院,山东淄博 255049)
基于S曲线加减速的NURBS插补控制方法研究*
岳 磊,赵国勇,刘晨希,安红静
(山东理工大学机械工程学院,山东淄博 255049)
对于复杂零件的数控加工,如何实现刀具轨迹的平滑插补控制具有重要意义。提出了一种基于S曲线加减速的平滑NURBS插补控制方法;采用复合辛普森求积公式计算NURBS刀轨曲线长度,并以最大轮廓误差、最大向心加速度为约束条件,对刀轨曲线进给速度进行规划。在此基础上,用二阶泰勒展开式进行NURBS插补计算,并对插补过程中的加速度、加加速度进行限制。仿真加工实例说明该方法可以实现平滑运动控制,并能够满足加工精度要求。
数控加工;S曲线加减速;NURBS平滑插补;加速度限制
0 引言
复杂零件的传统加工是先将加工路径分解成大量短直线或者圆弧,再进行插补加工,刀具轨迹曲线的很多几何性质如曲率在插补过程中丢失。因此面向复杂形状零件的数控加工,国内外众多学者研究了参数曲线插补方法。Koren等[1]提出了一种进给速度固定的参数曲线插补方法,Bedi等[2]提出了参数增量为定值的插补方法,但这两种方法速度波动很大。Yang等[3]提出了进给速度可变的参数曲线插补方法,使速度波动大幅度减弱,但是忽略了由进给速度的突变引起的加速度、加加速度变大带来的对数控系统的冲击。Nam等[4]提出了限制加加速度的加减速控制方法,用变化平滑的加速度曲线控制速度的突变,轮廓误差得到有效控制。S曲线加减速算法由于其在速度控制方面具有的较高柔性被越来越多地应用于NURBS插补的速度规划中。石川等[5]提出了一种七段式S曲线加减速方法,使速度和加速度保持连续。李晓辉等[6]提出了简化的七段式S曲线加减速算法,实时性较好。李建伟等[7]研究了一种S曲线实时前瞻算法,按曲线曲率进行分段,在每一分段内进行前瞻,确定减速点。周胜德等[8]提出了一种基于NURBS曲线插补的五段式S曲线加减速方法,较准确地预测了减速点。罗福源等[9]在S曲线加减速算法基础上,提出了插补路径未知情况下不依赖于弧长精确计算正反向寻优插补算法,使减速点的计算更加准确。
本文在前人研究的基础上提出一种基于5段式S曲线加减速的平滑NURBS插补控制方法,并以数控加工中的最大轮廓误差、最大向心加速度为约束条件,实现运动轨迹规划;采用迭代法求解减速点的位置,避免了分段进行速度规划;采用S曲线加减速方法,减小了陡坡处的进给加速度,有助于减小机床柔性冲击。
1 NURBS刀轨曲线长度的计算
任意一条k次NURBS曲线为一分段矢值多项式函数[10-11];
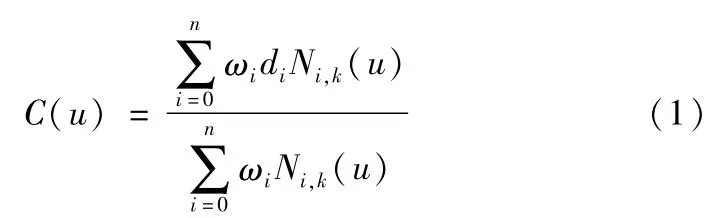
其中di称为控制顶点,ωi称为权值。Ni,k(u)是由节点矢量U=(u0,u1,…,un+k+1)决定的B样条基函数。采用复合辛普森求积公式计算NURBS曲线的长度,具体步骤如下;
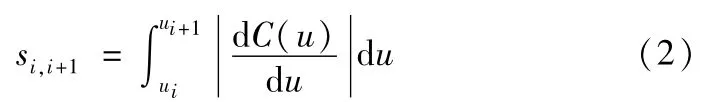
步骤2;NURBS曲线的总长度计算如下;

其中,K为曲线的次数,M为控制顶点数。
在得到刀轨曲线的长度L后,便可以进行速度规划,计算各个插补周期的进给速度。
2 S曲线加减速的速度规划
相对于常见的直线加减速、指数加减速方法,S曲线加减速模式没有速度突变,过渡平滑,加速度变化连续,可减小加工过程中的柔性冲击。典型的S曲线加减速模式分为5个阶段,如图1所示。

图1 S曲线加减速模式
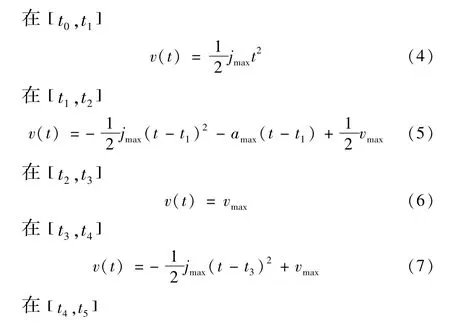
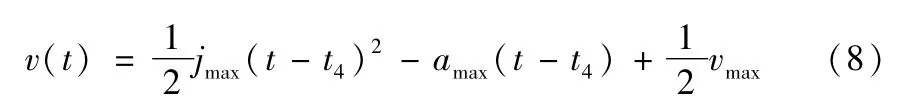
其中vmax为最大允许进给速度,jmax为最大允许加加速度,amax为最大允许加速度。
当整个运动轮廓恰好不含匀速运动段时,位移大小为

若加工曲线段长度L<S0,整个运行过程只有四个阶段,不含匀速运动段。一般情况下NURBS曲线的长度L≥S0,整个运行过程包含完整的5个阶段。对于不同的L,不同的只是匀速运动阶段的时间t;
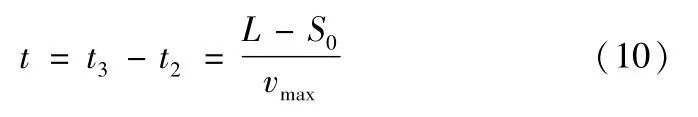
3 平滑NURBS插补计算
3.1 迭代法求解位置参数
对NURBS曲线插补的实质是就是不断的由当前的位置参数,在速度、加速度、曲线特性等条件的限制下,求下一插补点对应位置参数的过程。将参数u对时间t求导并将其按二阶泰勒级数展开,有
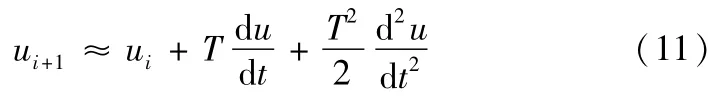
设C(u)为所要插补的二维NURBS曲线,其矢函数表达式为C(u)=(x(u),y(u)),则
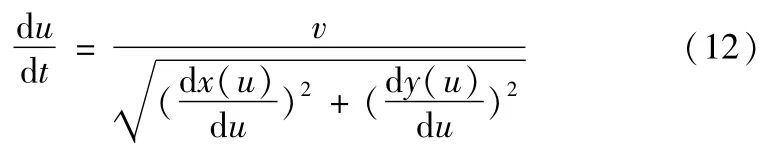
将上式再次取关于时间t的导数,得到
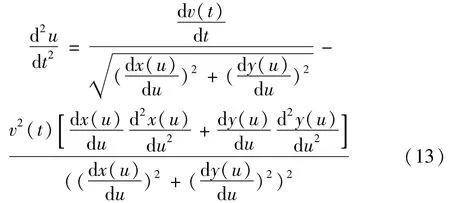
将式(12)、(13)带入式(11)中,便得到参数ui+1的二阶泰勒展开式。以得出的迭代公式,在给出初始条件后,不断迭代求出各个插补周期的位置参数u。
3.2 基于最大轮廓误差、最大向心加速度的速度自
适应控制
在NURBS插补过程中,对进给步长的控制实质就是对进给速度的控制。在最大轮廓误差δmax约束下,进给速度与最大轮廓误差的关系为;

当进给速度较大或者曲率半径较小时,向心加速度会比较大,有可能会超出机床的允许值。在最大向心加速度Amax约束下进给速度V;

3.3 加速度、加加速度限制
由于最大轮廓误差和最大向心加速度的限制,曲率超出一定值时,进给速度会急剧下降,形成一些速度陡坡。如图2所示。
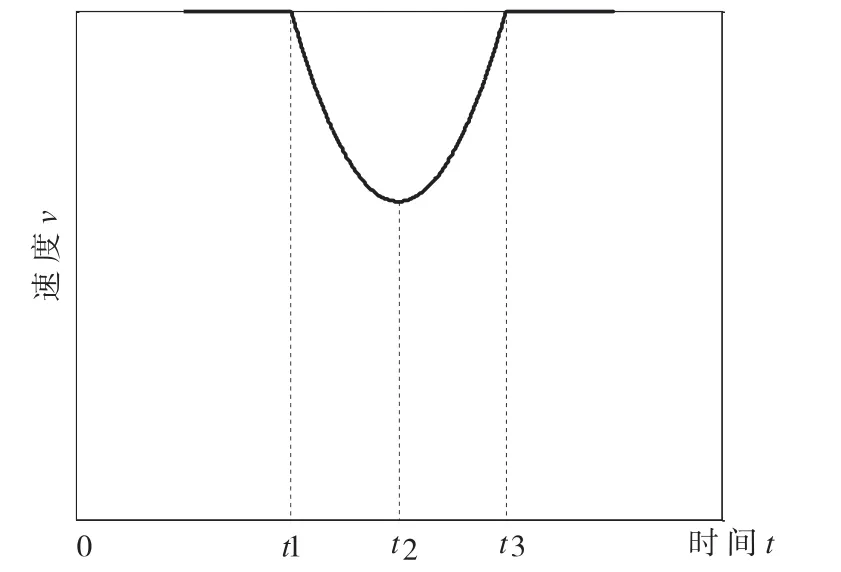
图2 速度陡坡示意图
在这些速度陡坡处因为速度急剧下降引起加速度和加加速度的突增,可能超过机床的承受能力,因而需要提前进行减速,从而减小最大加速度和加加速度。采用S曲线加减速方法,设减速前的速度为F,速度尖点处最小速度为vmin,则减速距离为;
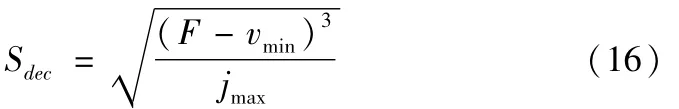
设初始减速点位置所对应的参数为udec,速度陡坡处对应的最小速度的位置参数为u,则

采用牛顿迭代法求解出udec。假设um<udec<um+1,以位移量S=2Sdec,最大速度Vmax=F-Vmin,运用S曲线加减速模式生成速度轮廓 V(um+n),若V(um+n)为一N维数组,则用S曲线型加减速平滑后的速度曲线为;

4 NURBS曲线插补实例
设所要插补的NURBS曲线如图3所示,参数如下;
次数k=3;控制顶点di;[5,5;21,10;49,16;58,50;70,80;91,50;100,10];节点矢量U;[0,0,0,0,0.2383,0.4229,0.5925,1,1,1,1];权值ωi;[1,1,2,1,0.1,1.8,1];设进给速度为12m/min,最大轮廓误差为1μm,最大进给加速度为4m/s2,最大加加速度为80m/s3,机床所允许的最大向心加速度为0.4g(g为重力加速度),插补周期为1ms。
仿真结果如图4到图7所示。可以看出在插补过程中,曲率越大,向心加速度和轮廓误差都越接近最大允许值。整个插补过程,进给速度变化平滑,随曲率的增大速度下降,整体进给速度接近最大值,并且波动很小。只在参数u=0.5附近,由于最大向心加速度的限制,速度降低(在陡坡处最大向心加速度达到最大允许值),并很快恢复到最大速度。
当采用基于S曲线加减速的NURBS插补方法时,对限制最大进给加速度和不限制最大进给加速度这两种情况进行对比分析,如图8所示。当不限制最大进给加速度时,如图8曲线1所示,进给加速度在速度陡坡附近发生突变,最大值接近5.8 m/s2,对机床造成较大的柔性冲击;当对最大进给加速度限制时,如图8曲线2所示,进给加速度小于4m/s2,一定程度上减小了对机床的柔性冲击。
结果说明本文提出的插补算法能够在允许的最大向心加速度和最大轮廓误差范围内,获得尽量高且变化平滑的进给速度,同时限制了在速度陡坡处的进给加速度突变,减小了机床柔性冲击。

图3 NURBS曲线的外形图
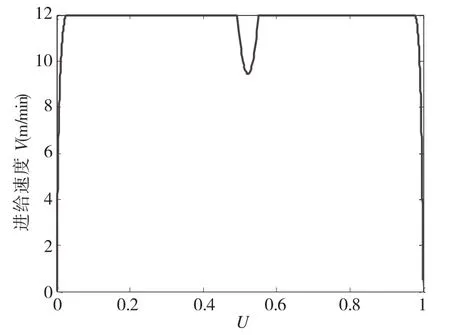
图4 进给速度图
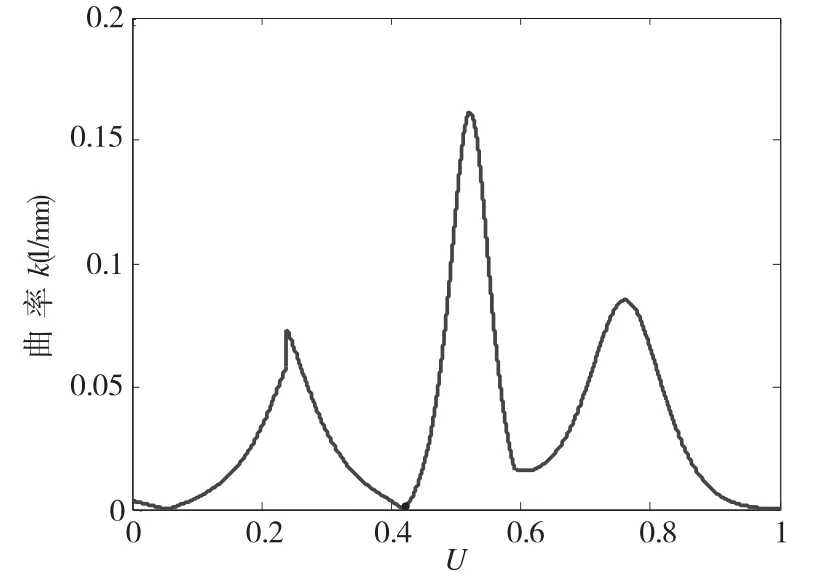
图5 曲率图
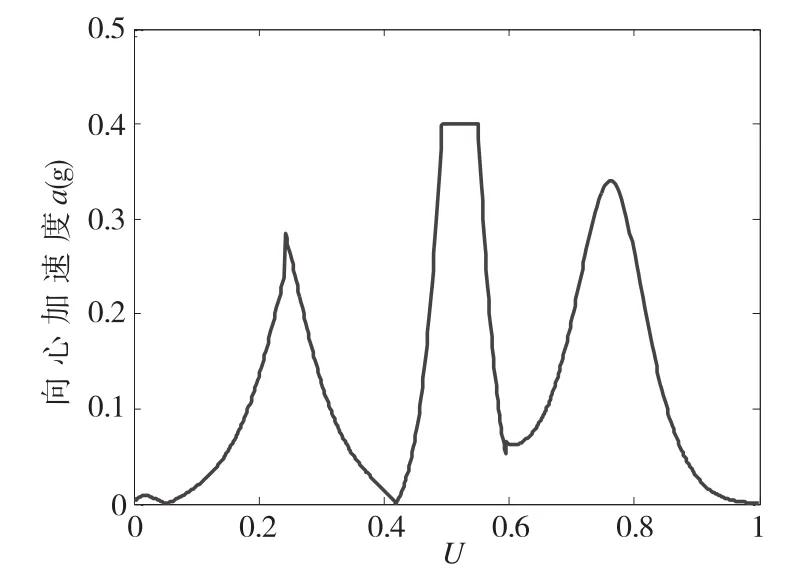
图6 向心加速度图

图7 轮廓误差图
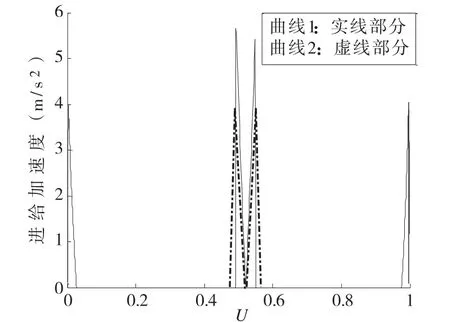
图8 进给加速度对比图
5 结束语
线性插补方法难以同时获得较高的加工精度和较高的进给速度,如何克服这一不足是数控加工领域的研究重点。提出了基于S曲线加减速的NURBS插补控制方法,能够获得较高且平滑的进给速度,在最大轮廓误差和最大向心加速度范围内,实现了插补精度和插补速度的双重优化,同时将最大加速度控制在机床允许范围,最后以仿真实例验证了方法的合理性和可行性。预计该方法能有效提高加工效率和加工质量,同时还能减小速度波动,改善机床工作环境。
[1]Y Koren,CC Lo,M Shpitalni.CNC Interpolators;Algorithms and Analysis[C]//Proceeding of the 1993 ASME Winter Annual Meeting;ASME,1993;83-92.
[2]BediS,Ali I,Quan N.Advanced interpolation tech-niques for CNCmachines[J].ASME Journal of Engineering for Industry,1993,115(1);329-336.
[3]CH Yang,T Kong.Parametric Interpolator Versus Linear Interpolator for Precision CNC Machining[J].Computer Aided Design(S0010-4485),1994,2(3);225-234.
[4]Nam Sung Ho,Yang Min Yang.A Study on generalized parametric interpolator with real-time jerk-limited acceleration[J].Computer-aided Design,2004,36(1);27-36.
[5]石川,赵彤,叶佩青,等.数控系统S曲线加减速规划研究[J].中国机械工程,2007,18(12);1421-1425.
[6]李晓辉,邬义杰,冷洪滨.S曲线加减速控制新方法的研究[J].组合机床与自动化加工技术,2007(10);50-53.
[7]李建伟,林浒,孙玉娥.基于S曲线加减速的NURBS实时插补前瞻控制算法[J].组合机床与自动化加工技术,2009(11);41-45.
[8]周胜德,梁宏斌,乔宇.基于NURBS曲线插补的五段S曲线加减速控制方法研究[J].组合机床与自动化加工技术,2011(4);37-41.
[9]罗福源,游有鹏,尹涓.NURBS曲线S形加减速双向寻优插补算法研究[J].机械工程学报,2012,48(5);147-156.
[10]赵国勇,徐志祥,赵福令.高速高精度数控加工中的NURBS曲线插补的研究[J].中国机械工程,2006,17(3);291-294.
[11]王海涛,赵东标,高素美.NURBS曲线实时插补中S型加减速算法的研究[J].山东大学学报(工学版),2010,40(1);63-67.
(编辑 李秀敏)(编辑 ;李秀敏)
Research on NURBS Curve Interpolation Method Based on S Curve Acceleration and Deceleration
YUE Lei,ZHAO Guo-yong,LIU Chen-xi,AN Hong-jing
(Department of Mechanical Engineering,Shandong University of Technology,Zibo Shandong 255049,China)
;For complex parts CNC machining,how to realize tool path smooth interpolation control is very important.A NURBS curve interpolation method based on S curve acceleration and deceleration is developed in the paper.The NURBS curve length is calculated with the compound Simpson quadrature formula;The tool path curve feed speed is planned within the limitation of the maximum perm is sible centripetal acceleration and the maximum permissible contour error.Then the NURBS curve is interpolated with the second-order Taylor expansion.The simulation machining results show that the introduced method can realize smooth motion control,and obtain satisfied machining precision.
;CNC machining;S curve acceleration and deceleration;NURBS smooth interpolation;acceleration limitation
TH165;TG659
A
1001-2265(2015)05-0043-04 DOI:10.13462/j.cnki.mmtamt.2015.05.012
2014-08-01;
2014-09-11
国家自然科学基金项目;五轴联动数控机床轮廓误差耦合控制理论与方法研究(51105236)
岳磊(1990—),男,山东济宁人,山东理工大学硕士研究生,研究方向为数控技术与装备;通讯作者;赵国勇(1976—),男,山东淄博人,
山东理工大学副教授,博士,研究方向为机械制造及其自动化技术,(E-mail)zgy709@126.com。
