微细铣削过程中刀尖径向总跳动度的实验研究

李光俊，高翼飞

（1.中国核电工程有限公司采购部，北京 100048；2.沈阳工业大学机械工程学院，沈阳 110870）

微细铣削过程中刀尖径向总跳动度的实验研究

李光俊1，高翼飞2

（1.中国核电工程有限公司采购部，北京 100048；2.沈阳工业大学机械工程学院，沈阳 110870）

微细铣削过程中，刀尖径向总跳动度与每齿进给量在同一量级，其影响切削过程切削厚度，从而影响切削过程切削力。文章基于轴向铣微孔实验分析了微细铣削过程中主轴转速和刀具悬伸量对刀尖径向总跳动度的影响规律，采用线性回归最小二乘估计法建立刀尖径向总跳动度预测模型，并对预测模型进行显著性检验和拟合度检验，检验结果表明：预测模型可用于切削参数范围内刀尖径向总跳动量的预测。

刀尖径向总跳动度；微细铣削；刀具悬伸量；主轴转速

0 引言

微细铣削技术具有加工材料范围广、能实现三维曲面加工、能耗小、设备投资少、效率高等诸多突出优点而成为近年来的研究热点［1-3］。微细铣削过程中微铣刀直径通常小于1mm，每齿进给量通常在微米量级［4］，为保证足够高的切削线速度，其主轴转速通常在几万甚至十几万转每分钟。由于刀具安装误差、刀柄制造误差及主轴自身径向跳动等因素的耦合作用导致刀尖相对于工件产生一个累积总跳动度［5］。较传统切削过程相比，微细切削过程中刀尖径向总跳动度与每齿进给量在同一量级，其对微细切削过程的影响不容忽视［6］。

刀尖径向总跳动度的测量及计算精度将直接影响切削厚度模型的建模精度，从而影响切削力的建模精度［7］。目前，已有部分学者对刀尖径向总跳动度做了部分研究，Schmitz等［8］采用分体结构耦合分析法建立高速铣削过程刀尖动态响应函数模型，Zhang等［9］、Filiz等［10］对动态响应函数模型的求解过程进行优化。目前的研究成果多以理论推导及有限元仿真为主，推导过程较为复杂且计算量较大，理论推导模型与实际切削过程有一定差距。

为避免繁琐的理论推导，精简问题研究，贴合实际应用，本文将采用实验分析方法分析主轴转速及刀具悬伸量对刀尖径向总跳动度的影响规律及程度；其次，基于试验结果建立刀尖径向总跳动度预测模型；最后，将对预测模型进行显著性检验和拟合度检验。本文建立的刀尖径向总跳动度预测模型将为后续切削厚度模型及切削力模型研究奠定基础。

1 刀尖径向总跳动度建模基础

机床主轴轴承及轴颈的形状误差是导致机床主轴产生纯径向跳动的主要原因［11］，刀具的安装误差、刀柄制造误差及刀具悬伸量对机床主轴径向跳动量有放大作用，最终表现为刀尖相对于主轴理想轴心的径向总跳动度。本文拟采用公式（1）来表述实际切削过程中刀尖径向总跳动度与主轴转速及刀具悬伸量之间的关系。

式（1）中；R为刀尖径向总跳动度（μm）；A为修正系数；b，c分别为主轴转速和刀具悬伸量对于刀尖径向总跳动度的影响指数。

建立刀尖径向总跳动度预测模型可以计算实验参数范围内任意主轴转速和刀具悬伸量下的刀尖径向总跳动度，对于建立切削力预测模型具有重要的参考价值。本文拟基于微细铣孔实验，采用线性回归最小二乘估计法识别公式（1）的系数，最终求解刀尖径向总跳动度的预测模型。

2 微细铣削过程刀尖径向总跳动度试验

2.1 实验设计

在微型数控铣床（如图1）上，通过铣微孔实验，研究微细铣削过程中主轴转速和刀具悬伸量（如图2）对刀尖径向总跳动度的影响。该微铣床采用精密高速电主轴，最高转速达140000rpm，电主轴径向跳动小于2μm；微径铣刀采用理论直径为0.6mm的超微粒子超硬合金涂层2刃平头立铣刀，刃长约为0.5mm，采用电子显微镜测量微铣刀实际直径为；D=594.1μm（如图3）。

图1 微型数控铣床结构图

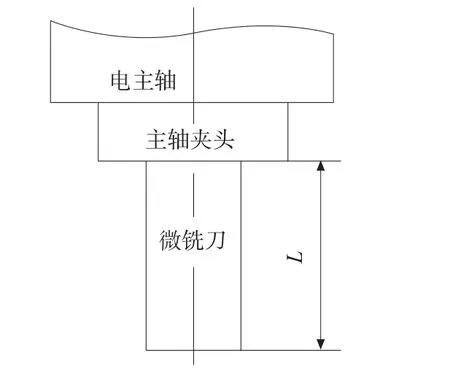
图2 刀具悬伸量示意图

图3 微径铣刀刀头SEM照片

微铣孔轴向切深为80μm，轴向进给速率为0.02mm/s。假设微铣刀实际直径为D，铣孔测量直径为Dm，则刀尖径向总跳动度为；R0=（Dm-D）/2。分别选取主轴转速和刀具悬伸量作为实验参数，如表1所示，研究各因素水平组合对刀尖径向总跳动度的影响规律。共做了36组实验，每组实验参数分别铣5个孔，去除测量偏差较大的坏点，选取实验测量结果的平均值作为该转速下的刀尖径向总跳动度。

2.2 实验结果与分析

各实验参数下的刀尖径向总跳动度实验测量结果如表1所示。依据表1实验数据，绘制刀具悬伸量及主轴转速对刀尖径向总跳动度的影响规律图如图4所示。

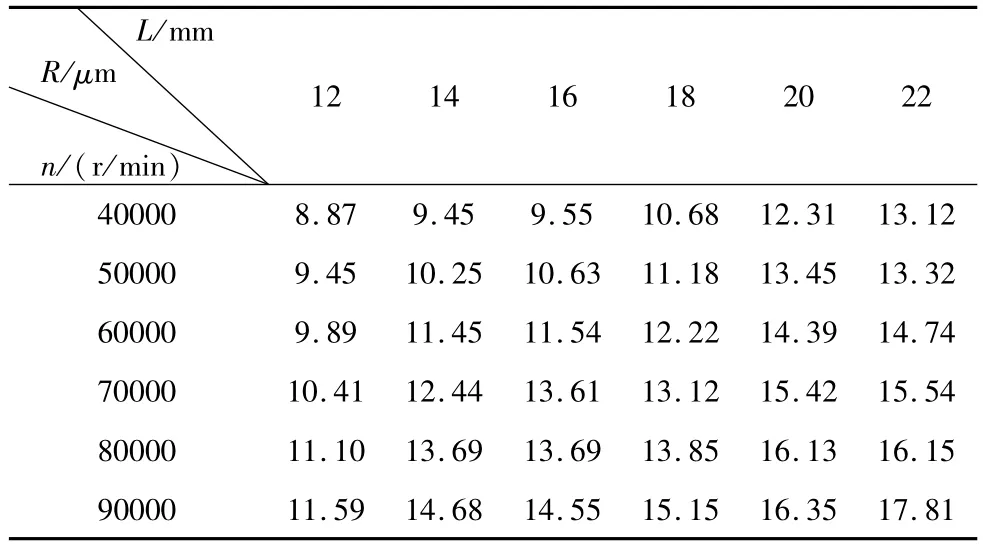
表1 刀尖径向总跳动度实验测量结果

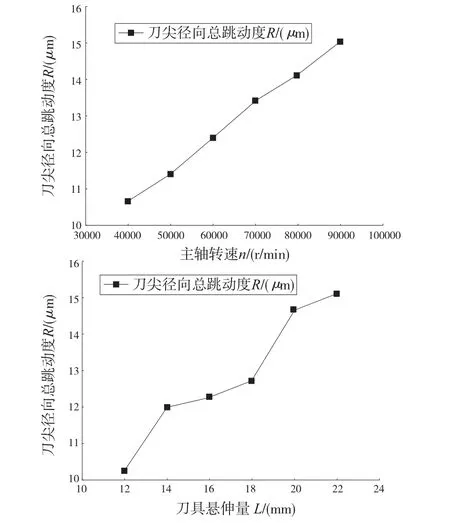
图4 刀具悬伸量及主轴转速对刀尖径向总跳动度的影响规律图

由图4可知；刀尖径向总跳动度随主轴转速的增加而逐渐增大，主轴转速增加，会使主轴径向跳动增大，同时加剧机床振动，从而使刀尖相对于工件的总跳动度增大。刀尖径向总跳动度随刀具悬伸量的增大出现先迅速增大后缓慢增大而后再迅速增大趋势，刀具悬伸量对主轴径向跳动、刀具安装误差及刀柄制造误差具有放大作用。当刀具悬伸量为14＜L＜18区域时，刀具悬伸量的变化对刀尖径向总跳动度的波动影响较小，切削过程较为稳定，在实际切削过程中建议选取此范围内刀具悬伸量参数。

3 刀尖径向总跳动度预测模型参数识别及验证

基于表1试验测量结果，采用线性回归最小二乘估计法对刀尖径向总跳动度预测模型公式（1）中的参数进行识别，最终求解的刀尖径向总跳动度预测模型如式（2）所示；

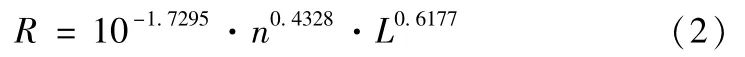
采用F检验法对回归方程进行显著性检验，得到方差分析表如表2所示。

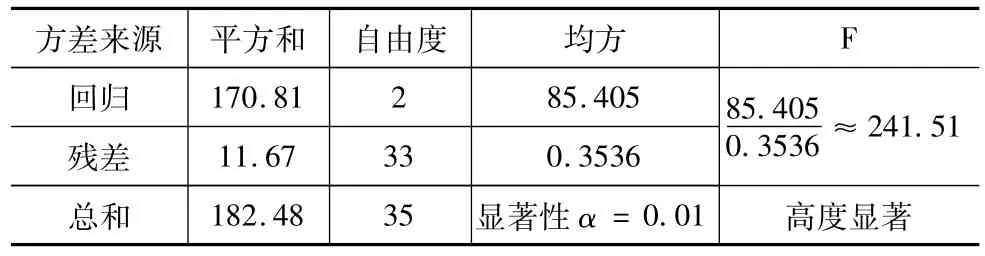
表2 回归模型方差分析表

回归方程显著性检验结果；F0.01（2，33）=5.32＜241.51，因此回归得到的刀尖径向总跳动度预测模型是高度显著的，且回归方程的相对拟合误差小于0.0963。回归方程高度显著，仅说明其在试验点处与实验结果拟合的好，不能保证回归方程的计算值在整个参数区域内与实测值拟合的好。为了验证建立的刀尖径向总跳动度预测模型的有效性和准确性，设计了15组实验对参数区域内的15个点进行回归方程的拟合度检验，测量值与回归方程理论计算值对比结果如表3所示。

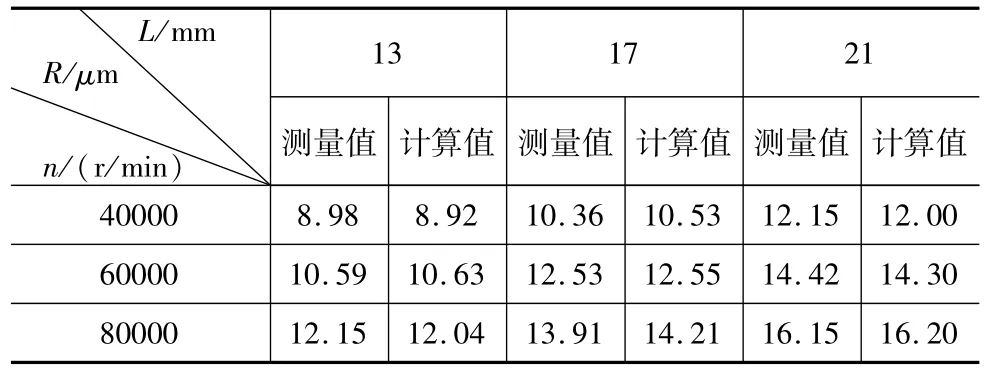
表3 拟合度检验点刀尖径向总跳动度实验测量值与回归模型计算值

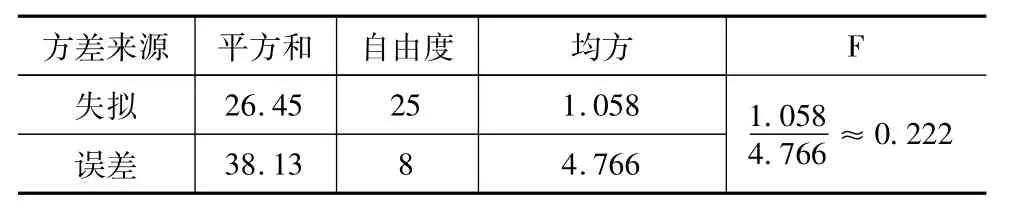
表4 回归方程拟合程度检验表

采用F检验法对回归方程进行拟合度检验，检验结果如表 4所示，由分析结果得；F0.01（25，8）= 5.27＞0.222，故刀尖径向总跳动度回归方程与实际实验测量值拟合的较好。

因此，所建立的刀尖径向总跳动度预测模型适用于参数范围为40000≤n≤90000；12≤L≤22内的刀尖径向总跳动度预测。

4 结论

本文基于微铣孔试验分析方法，分析了微细铣削过程中主轴转速和刀具悬伸量对刀尖径向总跳动度的影响，并建立预测模型，并对预测模型进行显著性检验和拟合度检验。

具体结论如下；

（1）刀尖径向总跳动度随刀具悬伸量及主轴转速的增大而增大；

（2）条件下测得的刀尖径向总跳动度最小为8.97μm，与微细铣削过程每齿进给量在同一量级，其对切削过程的影响不容忽略；

（3）基于试验结果，采用线性回归最小二乘估计法，建立的刀尖径向总跳动度预测模型可用于切削参数范围内刀尖径向总跳动量的预测。

本文的研究结论将对后续切削厚度模型及切削力模型研究奠定基础。

［1］高成秀，贾振元，卢晓红.微铣加工关键技术研究现状与发展［J］.组合机床与自动化加工技术，2012（1）；107-111.

［2］王利军，贾振元，卢晓红，等.立式微型数控铣床整机结构的有限元分析［J］.组合机床与自动化加工技术，2009（12）；12-20.

［3］JChae，SSPark，T Feiheit.Investigation of micro-cutting operations［J］.International Journal of Machine Tools& Manufacture，2006，46；313-332.

［4］X Liu，R EDevor，SG Kapoor.An analytical model for the prediction of minimum chip thickness in micro machining［J］.Transactions of the ASME，2006，128；474-480.

［5］Anon.Total indicated run out and its impact on combined board quality［J］.ATPPI Technical Information Papers，2002，190-192.

［6］HWang，STo，C Y CHAN.A theoretical and experimental investigation of the tool-tip vibration and its influence upon surface generation in single-point diamond turning［J］.International Journal of Machine Tools&Manufacture，2010，50；241-252.

［7］马万太，樊树海，楼佩煌.径向跳动对球面铣刀铣削力的影响研究［J］.中国机械工程，2005，16（24）；2171-2175.

［8］T L Schmitz，M A Davies，M D Kennedy.Tool point frequency response prediction for high-speed machining by RCSA［J］.Transactions of ASME，2001，123；700-707.

［9］JZhang，T Schmitz，W H Zhao，et al.Receptance coupling for tool point dynamics prediction on machine tools［J］. Chinese Journal of Mechanical Engineering.2011，24（3）；340-345.

［10］SFiliz，CH Cheng，K B Powell，etal.An improved tool holder model for RCSA tool-pint frequency response prediction［J］.Precision Engineering，2009，33；26-36.

［11］池宪，樊宁，高子辉，等.机床主轴纯径向跳动的轴心轨迹分析［J］.机械工程与自动化，2006（2）；7-9.

（编辑 李秀敏）

Research on the Tool-point Radical Run-out of Micro Milling Process

LIGuang-jun1，GAO Yi-fei2
（1.Procurement Department，China Nuclear Power Engineering Co.，Ltd.，Beijing 100048，China；2.School of Mechanical Engineering，Shenyang University of Technology，Shenyang 110870，China）

；In micro milling process，the tool-point radical run-out is comparable with the feed per tooth and w ill affect the chip thickness，ultimately impact the cutting forces.In this paper，micro drilling hole tests are carried out to analyze the influence principle of the spindle speed and the tool overhang on the tool-point radical run-out；and based on the test results，the tool point radical run-out prediction model is built by using linear regression least square estimation method.In addition，the significance test and fitting degree test are conducted on the prediction model，which show that the prediction model is efficient for predicting the tool point radical run-out in the range of test cutting parameters.

；tool-point radical run-out；micro milling；tool overhang；spindle speed

TH161；TG65

A

1001-2265（2015）05-0024-03 DOI：10.13462/j.cnki.mmtamt.2015.05.007

2015-01-26；

2015-02-06

李光俊（1988—），男，云南大理人，中国核电工程有限公司工程师，硕士，研究方向为微细铣削加工，（E-mail）andy1988lgj@126.com。