泥石流危险度的模糊物元评价方法
2015-11-01陈剑平刘志鑫
谭 春,陈剑平,徐 爽,刘志鑫
(1.中水东北勘测设计研究有限责任公司,吉林长春130061;2.吉林大学 建设工程学院,吉林 长春 130026)
泥石流危险度的模糊物元评价方法
谭春1,陈剑平2,徐 爽1,刘志鑫1
(1.中水东北勘测设计研究有限责任公司,吉林长春130061;2.吉林大学 建设工程学院,吉林 长春 130026)
泥石流是我国山区主要地质灾害类型之一,而泥石流危险度评价对于泥石流治理、防灾减灾对策的确定具有重要意义。本文在模糊物元分析原理的基础上,结合信息熵的概念,提出了基于熵权的模糊物元分析方法。在对泥石流危险度进行综合评价时,把危险等级作为物元的事物,以它们的各项评价指标及其相应的模糊量值构造复合模糊物元,通过关联度计算,实现对泥石流危险度综合评价。该模型被应用到乌东德泥石流综合评价中,分类结果与传统分类结果吻合较好,验证了该模型的分类性能良好,预测精度高,误判率低,是泥石流危险度分类的一种有效方法,可以在实际工程中进行推广。
泥石流;信息熵;模糊物元;危险度
泥石流是地质地貌灾害的一种主要类型,是山区常见的一种自然灾害现象。由于自然条件的复杂性,泥石流危险度划分受到多种因素的制约,并且这些因素之间的关系错综复杂,以不同的特征和相互组合产生综合影响,若以单个指标对泥石流危险度进行分类,其评价结果常常具有矛盾性、不确定性和不相容性。直接利用评价标准难以作出确切的评价,将遗漏一些有用的信息,甚至会导致错误的结论。20世纪80年代我国学者蔡文教授提出的物元分析理论是用于解决矛盾和不相容问题的有力工具[1,2]。本文在物元分析的基础上,结合信息熵的概念,建立了基于熵权的模糊物元分析方法,为泥石流危险度分类提供了一条新的途径。
1 模糊物元评价模型
1.1模糊物元和复合模糊物元
给定事物的名称N,它关于特征C有量值为v,以有序三元R=(N,C,v)组作为描述事物的基本元,简称物元。如果其中量值v具有模糊性,便称为模糊物元。如果事物N有n个特征C1,C2,…,Cn和相应的模糊量值v1,v2,…,vn,称R为n维模糊物元,简记为R=(N,C,V)。如果m个事物的n维物元组合在一起,使构成m个事物n维复合物元Rmn。若将Rmn的量值改写为模糊物元量值,称为m个事物n维复合模糊物元,记作

式中:R~为m个事物n维复合模糊物元;M为第imni个事物,i=1,2,…,m;Cj为第j项特征,j=1,2,…,n;μij为第i个事物第j项特征对应的模糊量值,即隶属度。
1.2泥石流危险度评价的隶属函数
众多的研究表明,分类参数的实测值均具有离散性,当观测次数较多时,可近似认为这些观测数据对同一类别的隶属函数为正态型,即:
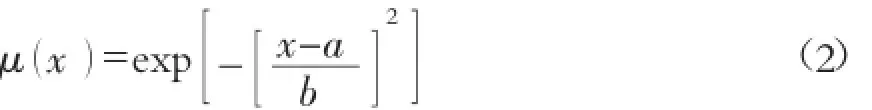
式中:a,b为常数,a>0,b>0。评价集是对泥石流危险度综合评价的语言表述。文献将泥石流危险度等级分为4个级别[3,4],本文选用该分类模式来建立泥石流的评价集,即V={Ⅰ,Ⅱ,Ⅲ,Ⅳ}={轻度危险,中度危险,高度危险,极度危险}。表1是根据文献结合乌东德地区将基本影响因素具体化后制成的单因素指标,它是确定中μij的基础。
由式(2),当x=a时,μ(x)=1,取最大值,显然,a是表1中因素参量对应区段的平均值。此外,表1中所给级别参量范围的边界值是从一种级别到另一种级别的过渡值,也是一种模糊边界,应同时属于对应的两种级别,即两种级别的隶属度相等,因此有
我国虽然是一个发展中国家,但是在公路施工期噪声的应对过程中,正保持高度关注,监测方法主要是表现在以下几项内容:第一,监测手段的开展必须进行多个监测点的有效布置。例如,部分地方的公路施工期噪声监测,之所以没有取得理想的成绩,很大一部分原因在于,监测点数量非常少,得到的结果和数据等,并不具备高度的准确性,由此产生的缺失较为严重。第二,监测工作的进行,要求进行不同时间点的针对性监测。从目前所掌握的情况来看,公路施工期噪声的出现是必然现象,但是由于受到施工时间的限制,以及周边环境的限制,在噪声的强度上会出现阶段性的变化,通过对不同时间段开展有效的监测,能够对未来防治工作,提供更多的参考和指导。
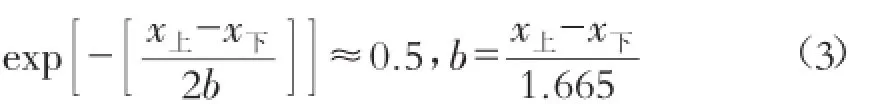
式中:x上,x下为对应级别的相应参数的上、下边界值。
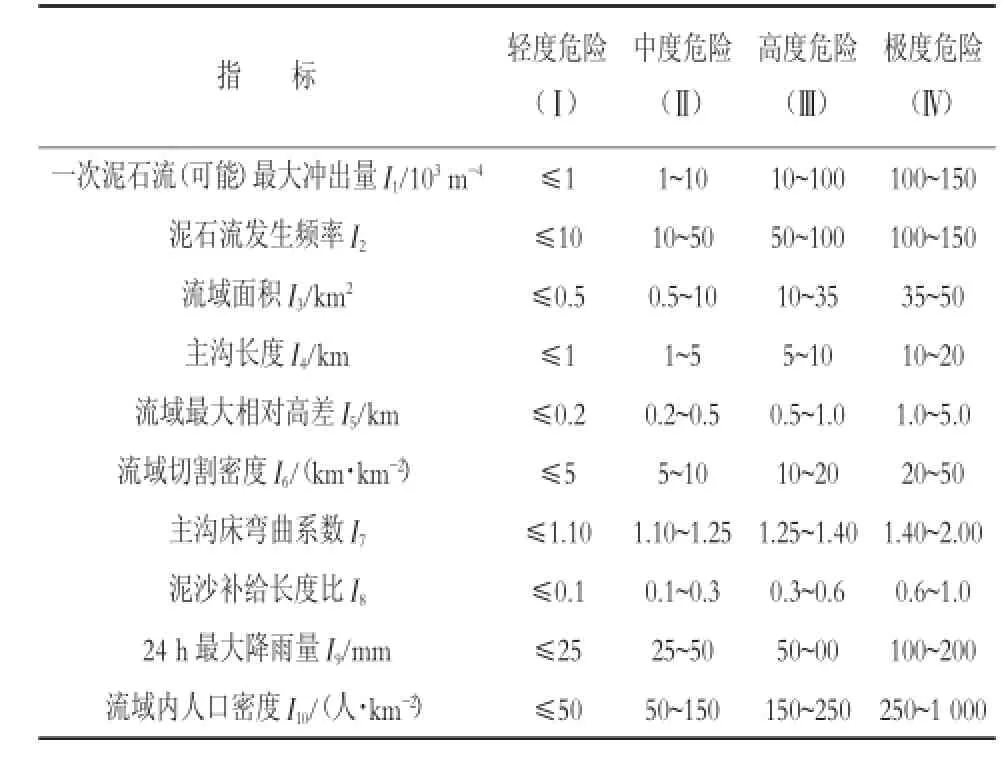
表1 泥石流危险度单因素指标
由表1,将计算结果列于表2。 这样,根据评价因素的实际观测值,把表2中的a,b值代入式(2)中,便可求得复合模糊物元中的各元素μij。
1.3关联变换
凡是以代数式来描述可拓集合量值的函数,称为关联函数。当关联函数中确知某一特定值时,就可求出相应的函数值,称此函数值为关联系数。关联系数与隶属度的相互转换称为关联变换。由于关联函数与隶属度等价,故关联系数可由隶属函数值(即隶属度)加以确定,因而有
ξij=μ(iji=1,2,…,m;j=1,2,…,n)(4)式中:ξij为第j个评价方案第i项指标的关联系数。
1.4建立关联系数复合模糊物元
根据关联变换,把式(1)中各个隶属度转换为相对应的关联系数,据此建立关联系数复合模糊物元,记为,即

1.5关联分析
考虑到本文综合评价的意义,采用M(*,+)算法,即先乘后加的运算模式。设表示m个关联度所组成的关联度复合模糊物元,则
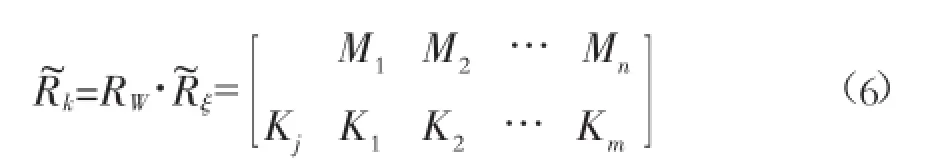
为每一方案各指标权重复合
物元;Wi为每一方案第i项评价指标的权重。根据最大关联度原则:K*=max(K1,K2,…,K1),即可确定泥石流危险度。
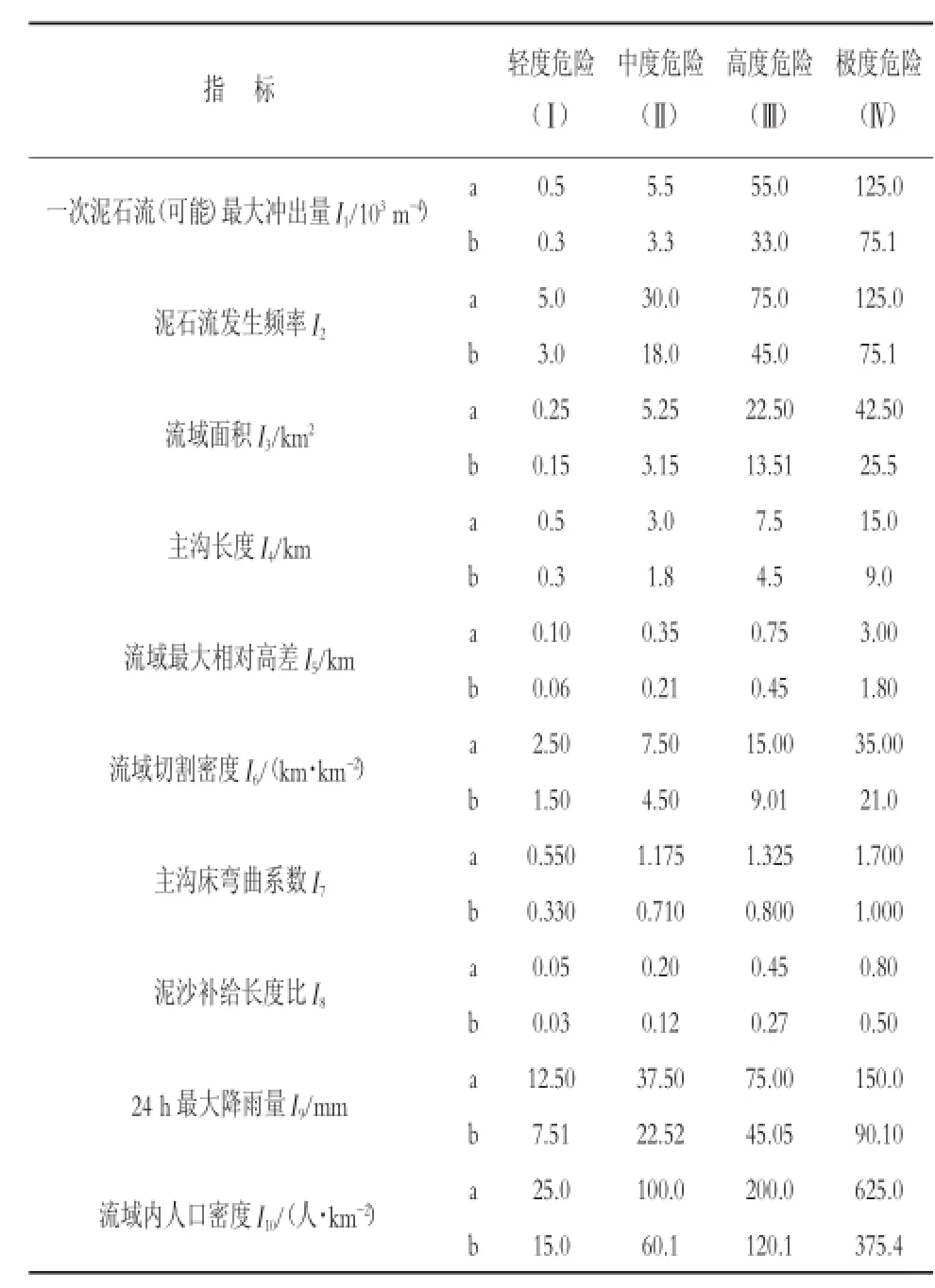
表2 泥石流危险度中μ(x)的a,b值
2 模糊物元评价模型
泥石流是一个开放的具有某种混乱度的系统,该系统受到众多因素控制,而各个因素所起的作用又是不确定的,而熵值法[5,6]能对一个系统状态混乱程度做出定量表示并可以客观地给出各个因素在系统中的重要程度,可以很好地应用于泥石流中,因此本文选择熵值法作为泥石流沟指标赋权的方法。
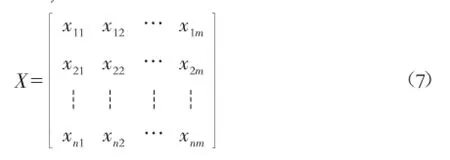
根据熵值法的原理,设有n个泥石流沟样本,m个影响因素,即评价指标,则评价指标特征值矩阵X=(xij)n×m为
1)对特征矩阵X进行归一化处理得到归一化矩阵R=(rij)n×m,由于各项指标具有越大越优型和越小越优型两种,因而所对应的归一化公式也不相同。对于越大越优型指标归一化公式为
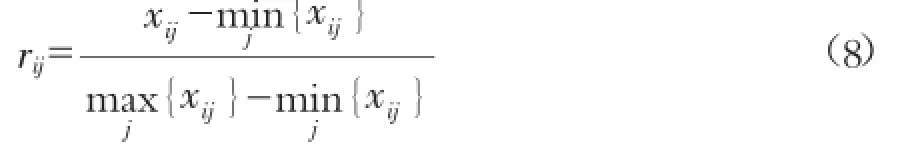
对于越小越优化型指标归一化公式为

由于是对泥石流沟的评价指标进行赋权,因此选择公式(8)进行归一化处理。
2)以第j个评价指标为例,第i个泥石流沟样本的特征比重P(xij)表达式:

3)由特征比重P(xij)就可以计算出指标j的熵值ej:

其中k>0,ej≥0,k=1/Inn,这样可以使ej∈[0,1]。
4)计算指标j的差异性因素gj,对于给定的指标j,若归一化矩阵中的rij差异性越小则ej越大,当rij都相等时,ej=emax=1,这种情况下指标j几乎无作用,对泥石流危险度没有影响,可以约简掉;反之,当rij差异性越大是ej越小,则j指标所起的作用越大,因此定义差异系数gj=1-ej。
5)计算出m个指标的熵值,然后就可以计算指标j的熵权wj,即:

3 工程应用实例
乌东德水电站是金沙江下游河段拟开发的4座大型电站之一。该区域位于青藏高原东南缘、川西南山地与云贵高原交接过渡地带,区域内有高山、峡谷、山间丘陵和平坝,并且受构造活动影响明显,物源极为丰富,植被覆盖率低,水土流失较严重,近几年来每年雨季均会发生规模大小不等的泥石流,泥石流潜在危险性较高。因此对乌东德地区泥石流危险度进行分类是十分重要的。
按照上述步骤,根据现场及遥感影像资料选取5条泥石流沟作为研究对象,参数指标见表3。
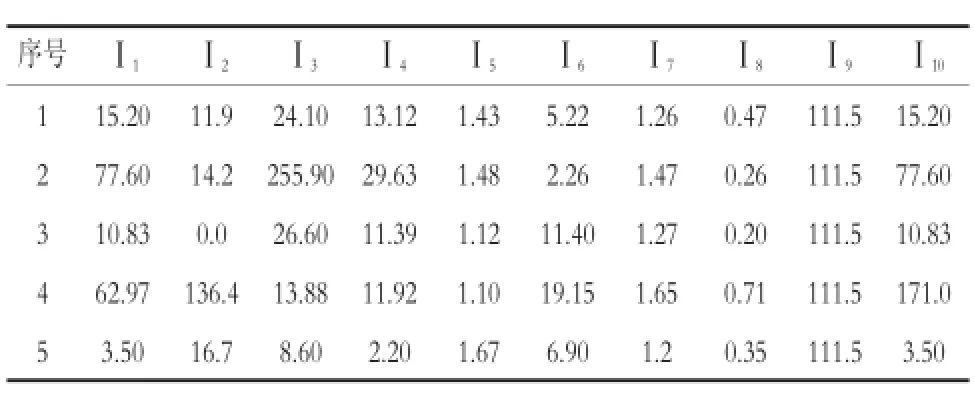
表3 泥石流参数指标值
3.1泥石流危险度的模糊物元
将泥石流危险度等级即轻度危险、中度危险、重度危险、极度危险分别记为M1,M2,M3,M4。将表2、表3中泥石流沟1的数据代入式(2),可构造出泥石流危险度评价的模糊物元为

3.2评价指标权重的计算
按照第2节所介绍的指标权重的确定方法进行计算,将泥石流沟样本参数由公式(7)到(12)计算得出的结果如表4所示。

指标 Ⅰ1 Ⅰ2 Ⅰ3 Ⅰ4 Ⅰ5 Ⅰ6 Ⅰ7 Ⅰ8 Ⅰ9 Ⅰ10权重 0 . 2 3 6 0 . 2 2 5 0 . 1 3 5 0 . 0 7 7 0 . 0 7 5 0 . 1 0 6 0 . 0 0 7 0 . 0 6 5 0 . 0 6 4 0 . 0 1 0
利用式(4)作关联变换,便得各方案每项指标相应的关联系数值,以此建立关联系数复合模糊物元为:
3.4计算关联度复合模糊物元
将权重和R~ξ代入式(6),可得关联度复合模糊物元,如表5所示。根据最大关联度原则,泥石流沟1为M3,即危险度为重度危险。按照此步骤对其余几条泥石流进行评价,评价结果如表5所示,与文献[7,8]评价结果一致。

表4 泥石流参数权重值
4 结 语
模糊物元分析理论以促进事物转化、解决模糊不相容问题为核心,适用于多因子评价问题,用于泥石流危险度评价克服了传统评价方法易于遗漏信息的缺点。基于信息熵理论的评价指标权重的确定方法,能更科学全面地考虑信息,是一种较为有效的方法,以此建立的模糊物元评价模型,使决策依据更加可靠、可信,有较大的应用价值。
[1]蔡文.物元模型及其应用[M].北京:科学技术文献出版社,1994.
[2]张斌,雍歧东,肖芳淳.模糊物元分析[M].北京:石油工业出版社,1997.
[3]刘希林,唐川,陈明,等.泥石流危险范围的模型预测法[J].自然灾害学报,1993,2(3):67—73.
[4]刘希林.泥石流危险度判定的研究[J].灾害学,1988(3):10—15.
[5]孙慧钧.关于权数与赋权方法分类的探讨[J].东北财经大学学报,2009(4):3—7.
[6]魏书堤,姜小奇.一种利用信息熵确定属性权重的模糊单因素评价方法[J].计算机工程与科学,2010,32(7):93—107.
[7]张晨,陈剑平,王清,谷复光,张文.乌东德地区泥石流危险范围预测模型[J].吉林大学学报(地学版),2010,40(6):1365—1370.
[8]张文,陈剑平,秦胜伍,张晨,李明,马建全.基于主成分分析的FCM法在泥石流分类中的应用[J].吉林大学学报(地学版),2010,40(2):368—372.
TV144
A
1002-0624(2015)12-0007-03
2015-08-14
