非正弦周期电压的教学探讨
2015-11-01苏立波王维建
苏立波 周 波 王维建
(兴义民族师范学院, 贵州 兴义 562400)
非正弦周期电压的教学探讨
苏立波 周 波 王维建
(兴义民族师范学院, 贵州 兴义 562400)
在线性电路中,利用傅里叶级数把电源产生的非正弦周期电压分解为一系列不同频率的正弦电压,分别计算在一种频率的正弦电压单独作用下一个电路元件上的电压分量,再根据叠加原理对所有电压分量进行叠加,从而得到这个电路元件上的实际电压。这就是工程技术中经常采用的谐波分析法。
非正弦周期电压;傅里叶级数;叠加原理;谐波分析法
在《电工电子学》课程的教学中,傅里叶级数的应用是学生在学习过程中遇到的一个主要障碍。从三角函数的正交性入手,运用基本积分公式推导傅里叶级数的系数计算公式是有效突破这一教学难点的关键环节。
一、三角函数的正交性
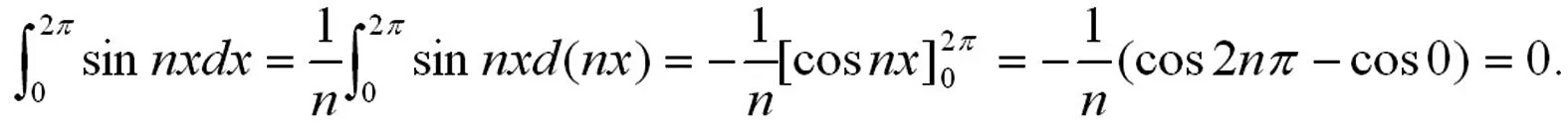
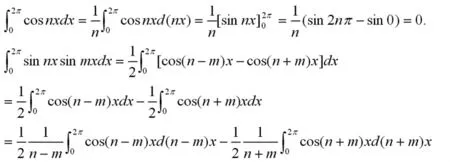
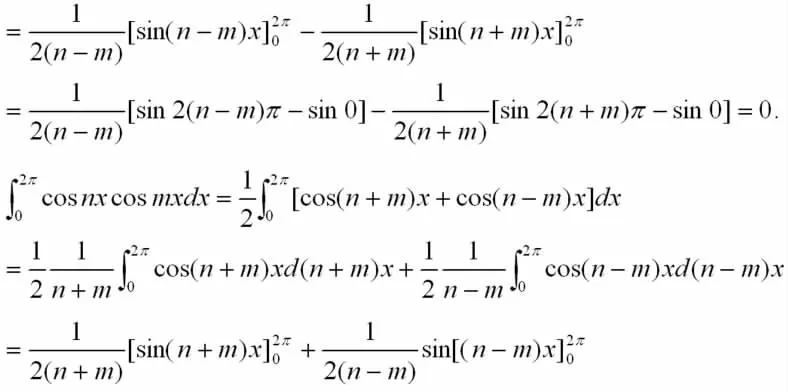
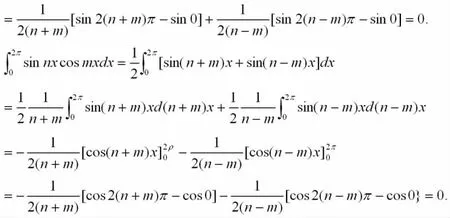
三角函数的正交性是推导傅里叶级数展开式中系数计算公式的数学基础。
二、傅里叶级数



为了确定系数bk,在展开式两边的各项上乘以后再利用三角函数的正交性对时间进行积分

正确理解傅里叶级数展开式中系数计算公式的推导过程可以帮助学生更好地运用傅里叶级数对交流电路进行分析。
三、非正弦周期电压的分解
1.全波整流电压
正弦交流电压通过桥式整流电路后变换为全波整流电压。下面把全波整流电压展开成傅里叶级数。

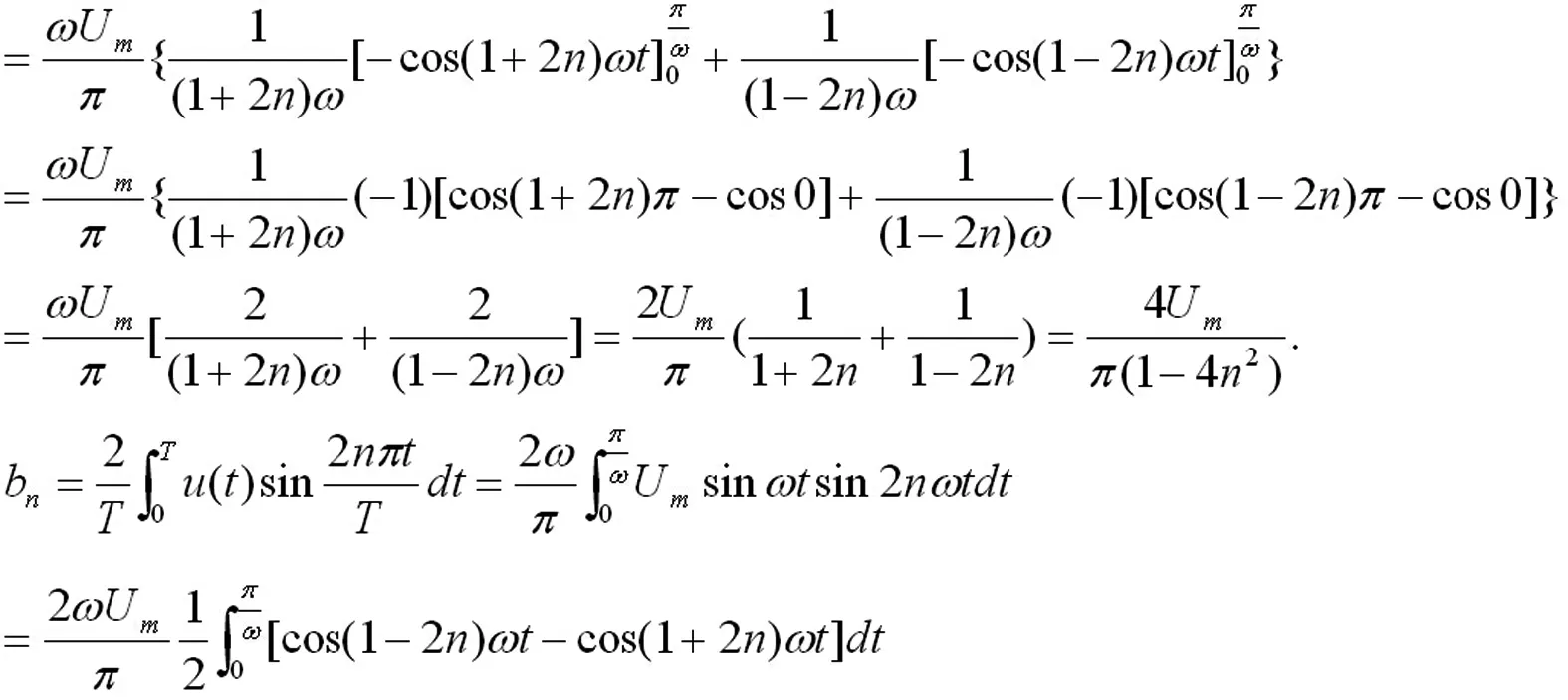
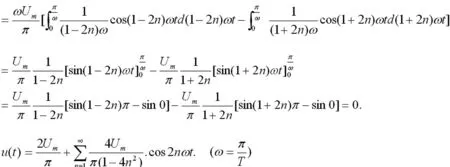
全波整流电压的傅里叶展开式中包含直流分量和偶数次余弦谐波分量,并且谐波电压分量的幅值随着频率的升高而迅速减小。
2.方波电压
正弦交流电压通过过零比较器后变换为方波电压。下面把方波电压展开成傅里叶级数。


方波电压的傅里叶展开式中没有直流分量,只包含奇数次正弦谐波分量,并且谐波电压分量的幅值随着频率的升高而依次减小。
3.锯齿波电压
方波电压通过积分电路后变换为锯齿波电压。下面把锯齿波电压展开成傅里叶级数。

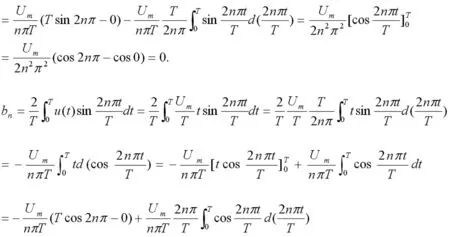
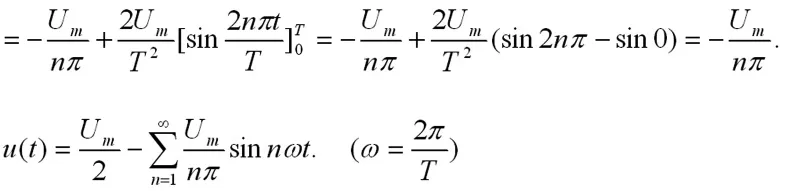
锯齿波电压的傅里叶展开式中包含直流分量和正弦谐波分量,并且谐波电压分量的幅值随着频率的升高而依次减小。
四、非正弦周期电压的谐波分析

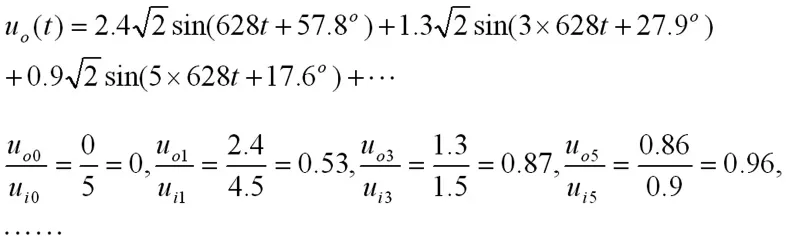
在输出电压中没有直流分量,只包含奇次谐波。随着谐波频率的升高,电容的容抗依次减小,谐波输出电压分量与输入电压分量之比增大,所以高次谐波很容易从电路中通过。
傅里叶级数在工程技术中有着广泛的实际应用。在电力工程中经常会遇到周期性的电讯号,在通讯工程中经常使用各种形式的电脉冲,在研究波动、传热这些物理现象的时候,最主要的数学工具也是傅里叶级数。
[1]叶挺秀编.电工电子学(第四版)[M].高等教育出版社,2014.
[2]四川大学数学系编.高等数学(物理类专业用、第三版)[M].高等教育出版社,2005.
[3]梁昆淼编.数学物理方法(第四版)[M].高等教育出版社,2010.
责任编辑:杨合成
Harmonic Wave Analysis of None-Sine Cyclic Voltages
SU li-bo ZHOU bo WANG wei-jian
(Xingyi Normal University For Nationalities,Xingyi Guizhou 562400 China)
In a linier electric circuit,a non-sine cyclic voltage created by electric source can be divided intoa series of sine voltages with different frequencies depending on the application of Fourier series.We can calculate the voltage element on one electric circuit unit acted separately by a single sine-voltage and add all the voltage elements together on the base of addition principle.Thus the real voltage on this electric circuit unit is obtained.This is the harmonic wave analysis method ordinarily used in engineering and technology.
non-sine cyclic voltage;Fourier series;addition principle;harmonic analysis method
1009—0673(2015)05—0094—07
TM131.3-4
A
2015—09—15
苏立波(1962— ),男,湖南浏阳人,兴义民族师范学院物理与工程技术学院讲师,主要从事大学物理教学研究。
