无线传感器网络覆盖空洞修复策略

2015-11-01曾雅丽赵福双

中国科技信息 2015年9期

曾雅丽赵福双

无线传感器网络覆盖空洞修复策略

曾雅丽赵福双

随着通信技术的发展，传感器网络给人们带来了越来越多的便利。当传感器网络中随意一个节点因它自带的电能消耗尽或者监测的目标区域环境被破坏而失去通信功能，可能导致网络出现覆盖空洞而无法通信。覆盖空洞会使邻居节点能耗速度加快而死亡，使得无线传感器网络的覆盖质量和通信效果变得不好，只有采用有效方案修复覆盖空洞或对网络重新部署，才能提高网络资源利用和延长网络使用时间。

无线传感器网络是由大量传感器节点构成的无线网络，其构成方式是以自组织和多跳的方式，其任务为在网络覆盖区域中的收集到的数据信息发送给数据使用者就是终端用户如图1。传感器网络节点操控的数据在行经其他节点逐跳传达，在传达的过程中数据或许会被节点处理过，经过很多跳到汇聚节点最后通过互联网或移动通信网络到达具有管理功能的节点，终端用户用管理节点就可以操控网络，全程的关键问题是对目标监测区域实现覆盖。

移动传感器网络是由在需要采集信息的地方散开的可以移动的节点构成，可以根据节点准确的感知条件以及其通信功能实现节点的动态分布。与传统的静态传感器网络相比，拥有移动能力的传感器网络有覆盖面积更大、对数据的反应速度快、获取信息可靠性较高等特点。现在静态的传感器网络有很多不足，例如获取信息的能力不强、对巨大的数据不能进行处理、无法快速勘测目标监测区域环境特征等等。

研究及发展概况

图1　无线传感器网络图

传感器节点在能量耗尽时可能会导致网络产生覆盖空洞。覆盖空洞的存在会使空洞边缘节点的能量消耗增加，节点死亡的速度增加，导致网络覆盖质量下降以及节点之间连通性降低，这样一来整个网络都会失去通信功能不能传输信息了，但仍然还有大很多节点没有被使用到。

在大部分静态传感器网络中使需要采集信息的地方每个节点对象都被k（k≥1）个节点覆盖，多重覆盖使得许多节点在能量消耗结束不起作用后，网络仍然能保证需要采集信息地区的网络密度，这样的话在恶劣的条件下传感器网络能提高它的生命力。但是很多节点在同一时间都作用一个目标节点这会浪费节点的数量浪费成本。文献选择了空洞边缘节点数目很多的冗余节点进行激活来修复覆盖空洞，但该算法在一方面没有周全考虑冗余节点的利用效率，另一方面忽略了多重覆盖会形成很多经济损失。

移动节点用时最少算法

算法概述

针对覆盖空洞可以采取移动冗余节点进行修复，但移动的过程中会有能量的消耗，怎样移动才能达到减少能耗又能修复空洞的目的？结合最小生成树的思想提出了用时最少的算法，该算法的中心思想是当探测到无线传感器网络中存在覆盖空洞，选取一个空洞边缘节点作为移动节点，移动一个边缘节点到空洞范围内的网络节点位置上，采取激活它能获取信息的范围距离内位置信息最好的冗余节点进行修复覆盖空洞。

图2　闭合空洞图

问题描述

主要考虑已经探测到无线传感器网络中覆盖空洞大小及位置信息情况下，怎么唤醒冗余节点进行覆盖空洞修复。在图2，节A-H以及节点M都是空洞边缘节点，相互邻接成闭合空洞区域，图中红色节点M为可移动节点，利用可移动节点行经空洞中唤醒其通信范围内的冗余节点，根据可移动节点M的行走的路径可以随机选择则可产生最优的路径，使得其修复时间最短。

存在如下两种情况如图3。

1.当移动节点M移动到覆盖空洞中网络节点位置时，冗余节点在其通信范围内，则可将其唤醒。

2.当移动节点M移动到覆盖空洞中网络节点位置时，冗余节点不在其通信范围内，即冗余节点在其通信范围以外，在这样的情况下查找其附近具有通信功能的冗余节点，计算出移动节点与能通信的冗余节点之间的距离选择合适的位置重新部署一个具有通信功能的节点，使得两网络节点间能相互通信。如图4，移动节点M移动到节点1的位置，冗余节点2不在其通信范围内，节点3为其附近具有通信功能的节点，节点N是节点1与节点3距离之间选取的合适位置，部署的新节点N的通信半径为R，达到唤醒节点3且使得网络能够相互通信的目的。圆1与圆3与圆N的交点分别为a，b。

图3　移动节点分类图

图4　唤醒节点图

图5　Kruskal算法步骤图

算法描述

（1）最小生成树Kruskal算法过程如图5。

（2）最小生成树Prim算法过程如图6。

实验验证算法的优势

我们分别对三种算法进行对比：最小生成树Kruskal算法，最小生成树Prim算法以及普通移动节点算法。对比结果如表1。

图6　Prim算法步骤图

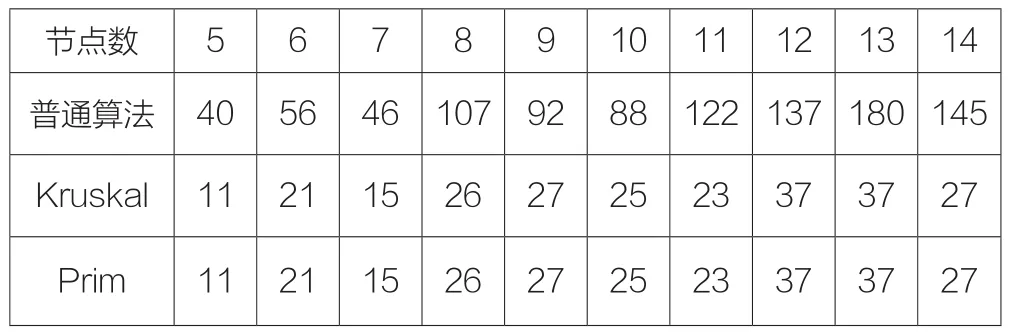
表1　三种算法权重值图

如表1随着随机产生节点数的不同，采用Kruskal，Prim两种算法所得权重相等也就意味着采用两种进行修复所移动的距离是相同的，但都比普通算法所移动的距离少，即达到减少移动节点移动的距离来节约能量进行修复空洞的目标。在此过程中需要考虑时间因素，因为在移动相同距离，速度相同的情况下，只有时间最少的才能决定哪个算法更优，因为节点在移动的过程中会消耗能量，移动的时间越少能量消耗越少，使用减少时间达到更优修复空洞的目的。分析两种的时间复杂度可知，Prim算法的时间复杂度为O（n2），Kruskal算法的时间复杂度为O（eloge）（e为边的数量），综合来说Kruskal算法比较适合边数较少的时候，Prim算法比较适合边数较多的时候，也就是说在节点较多时最佳选择是Prim算法。