基于复杂网络的指控系统信息网络拓扑结构研究
2015-11-01杨海涛何宇
杨海涛 何宇
1.装备学院复杂电子系统仿真实验室,北京,101416 2.装备学院信息装备系,北京,101416
当今因特网(Internet)的前身是美苏冷战期间美国军方提出的分组交换网.该网络在战争期间即使某一部分因遭受攻击而失去工作能力,网络的其他部分仍然能够维持正常的通信.因此,ARPANET应该算是指控系统信息网络的“鼻祖”.随着网络科学[1−2]的发展,Internet也逐渐作为复杂网络的代表,成为研究对象.除信息网络外,实际的指控系统也成为复杂网络的研究对象.美英联军通过对指控系统中使用的电子邮件系统进行研究[3],发现邮件系统具有与无标度网络相似的特性;朱涛等人[4]通过演习数据也发现指控信息系统具有小世界和无标度特性;同时,文献[5−12]基于复杂网络对指控系统相关网络进行了建模研究.
1 考虑网络性能的拓扑演化模型
通常情况下,任何工程网络在构建时都有一定的网络性能要求,虽然网络性能的指标很多,但也有一些公认的设计目标[13]可供参考.针对分组交换信息网络,本文主要选取了构建成本、网络时延、鲁棒性和吞吐量作为主要考虑的因素.
1.1 主要因素归一化度量
1.1.1 构建成本归一化度量
无论是有线链路还是无线链路,在相同的技术条件下,节点之间的距离始终是决定成本的重要因素.因此,这里采用节点间的距离作为构建成本的度量.
设新节点m与网络中已存在节点i之间的距离为di.若最小距离记为dmin,最大距离记为dmax,则节点m与节点i建立连接的构建成本归一化度量为
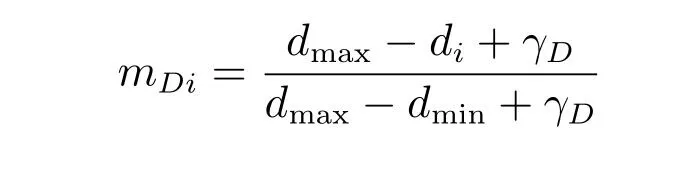
其中,γD为控制参数
1.1.2 时延归一化度量
采用网络中节点之间的平均最短路径长度作为网络时延的度量.
设新节点m与网络中已存在节点i建立连接后,网络的时延为hi.若最小时延记为hmin,最大时延记为hmax,则节点m与节点i建立连接的网络时延归一化度量为(其中,γH为控制参数)
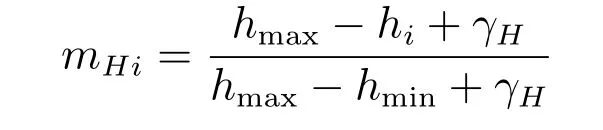
1.1.3 鲁棒性归一化度量
采用网络受到一定破坏后仍能够连接通信的节点对数比例作为网络鲁棒性的度量.
设新节点m与网络中已存在节点i建立连接后,网络受到一定程度的破坏后仍能够进行通信的节点对数比例为ri.若最小比例值记为rmin,最大比例值记为rmax,则节点m与节点i建立连接的网络鲁棒性归一化度量为(其中,γR为控制参数)
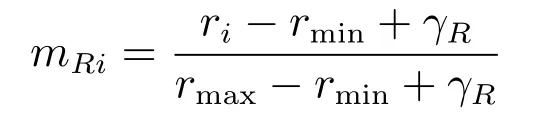
1.1.4 吞吐量归一化度量
采用网络的临界信息产生率[14]作为网络吞吐量的度量.
设新节点m与网络中已存在节点i建立连接后,网络的吞吐量为ti.若最小吞吐量记为tmin,最大吞吐量记为tmax,则节点m与节点i建立连接的网络吞吐量归一化度量为(其中,γT为控制参数)
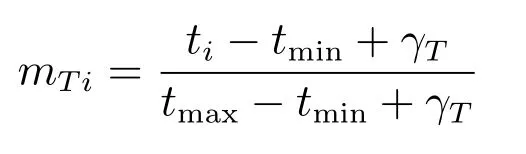
1.2 演化模型
考虑二维区域Lx×Ly,初始网络有m0个节点(节点具有位置属性)和e0条边.每一时间步产生一个具有位置属性(xi,yi)的新节点i,节点i按照约定规则与m个已有节点建立连接,直至演化的网络达到指定规模.每一时间步的网络演化规则如下:
1.2.1m值的确定
当一个新节点加入网络时,需要确定其与网络中的几个已有节点建立连接.设所生成最终网络的平均度为,每个新节点加入网络时可以与k∈{1,2,···,maxk}个网络中已有节点建立连接,其中maxk为正整数.设k=i的概率为pi,其中i∈{1,2,···,maxk},则pi需满足以下关系
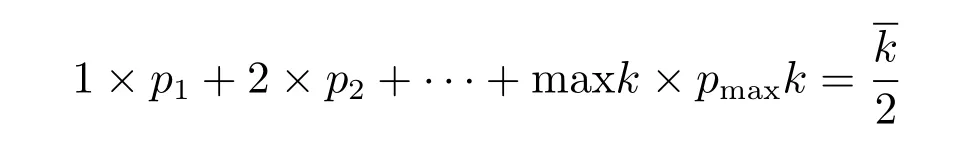
1.2.2 连接策略
设网络构建过程中侧重于构建成本的权重为wD,侧重于时延的权重为wH,侧重于鲁棒性的权重为wR,侧重于吞吐量的权重为wT,则新加入节点与具有最大连接判断度量measure且没有与之建立链路的节点i建立链路.如果有多个备选节点符合此条件,则随机选取一个备选节点与新节点建立连接.其中,
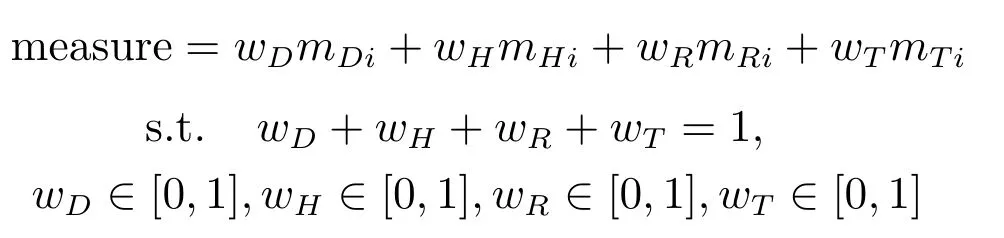
2 数值仿真分析
设置网络的节点数为300,节点随机分布在1×1的区域,平均度为3.98,采用按介数中心性从大到小的顺序攻击20%节点的效果来度量网络的鲁棒性.演化模型权重的取值为
由于某一权重取固定值时可能有多种组合都满足约束关系,因此,这里将对每一权重取固定值时的多种组合所得的平均值进行分析.
2.1 累积度分布幂律拟合相关系数绝对值和拟合指数
通过分析计算结果,可得累积度分布幂律拟合相关系数绝对值(Absolute Correlation Coefficient:ACC)与各权重之间的关系,如图1所示.如果以ACC≥0.8(图中横线所示)为满足幂律分布的标准,可以看出并不是所有权重组合所生成网络的累积度分布都符合幂律分布.但是,绝大部分的权重组合所生成网络的累积度分布满足幂律分布(本例中所占的比例为73.05%),并且几乎所有满足幂律分布的累积度分布拟合指数都小于等于3,如图2所示.
2.2 平均最短路径长度
通过分析计算结果,可得平均最短路径长度与各权重之间的关系,如图3所示.从图3(a)∼图3(d)可知,wD、wR和wT发生变化对网络时延的影响不大;从图3(b)可知,平均最短路径长度随着wH的增大而减小.
2.3 平均集聚系数
通过分析计算结果,可得平均集聚系数[15]与各权重之间的关系,如图4所示.从图4(a)∼图4(b)可知,网络平均集聚系数随着wD和wH的增大而增大;从图4(c)∼图4(d)可知,网络平均集聚系数随着wR和wT的增大而减小.
3 结论
从数值分析可知,在一定网络规模下,不同工程性能因素权重对指控系统信息网络的结构特性具有不同的影响,但是在大多数情况下构成的网络拓扑结构仍具有满足幂律分布、幂律指数小于或等于3和小世界等实际复杂网络所具有的特性,这对指控系统信息网络拓扑的构建具有重要的参考意义.下一步将加强对该模型解析解及优化的研究.
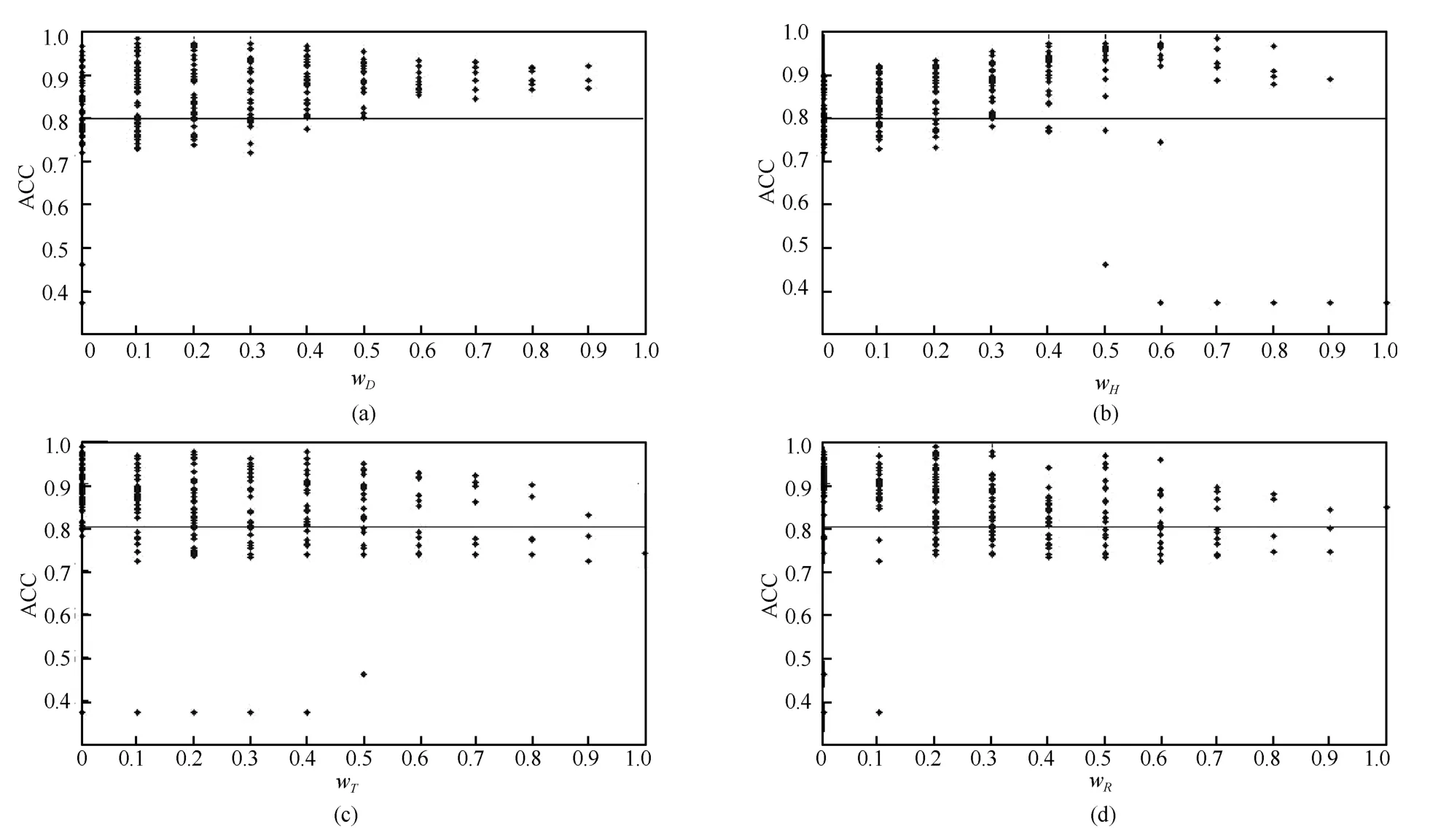
图1 累积度分布幂律拟合相关系数绝对值与各权重的关系
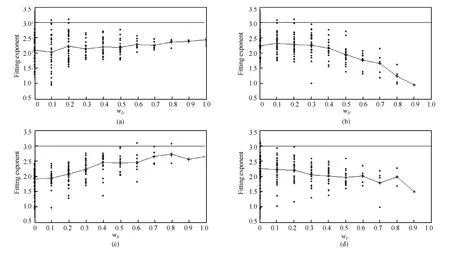
图2 累积度分布拟合指数与各权重的关系
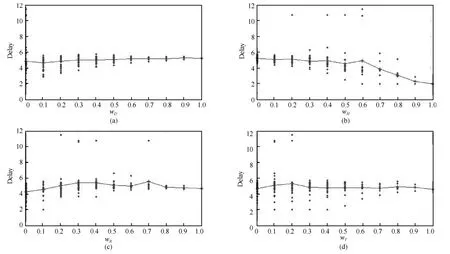
图3 平均最短路径长度与各权重的关系
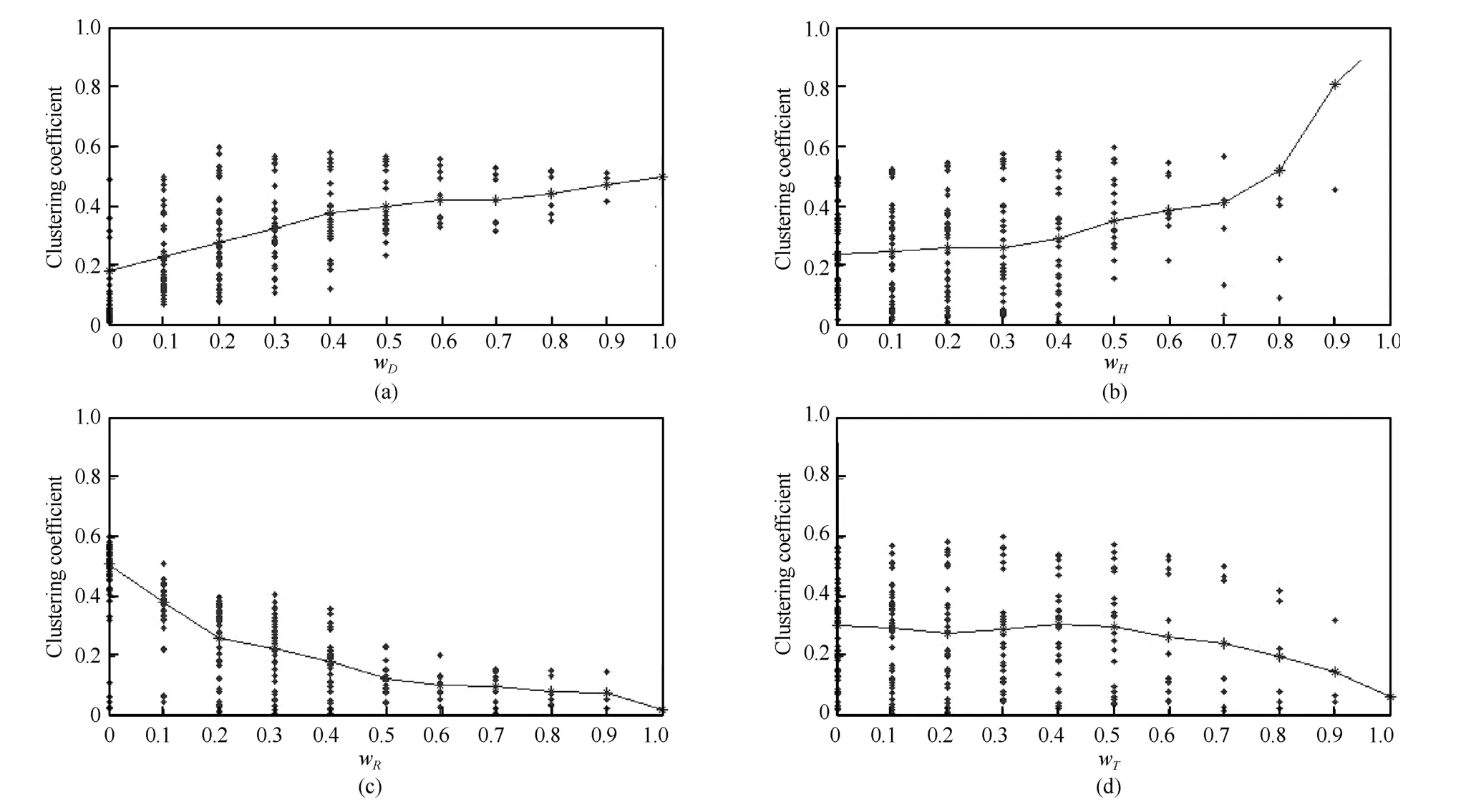
图4 平均集聚系数与各权重的关系