基于最短路径的变半径泊车路径规划研究

王龙，朱凯

（1.重庆交通大学机电与汽车学院，重庆 404100；2.中国农业大学工学院，北京 100083）

基于最短路径的变半径泊车路径规划研究

王龙1，朱凯2

（1.重庆交通大学机电与汽车学院，重庆 404100；2.中国农业大学工学院，北京 100083）

自动泊车路径的规划属于从低约束到高约束的问题，也属于非完整约束问题。一般的路径规划总是不尽如人意，对泊车条件要求高。根据一般问题的解决从高约束到低约束的过程，在最短路径的基础上，先确定高约束阶段泊车车辆进入泊车位的路径，计算出停车位长度与直线斜率的拟合公式，得到直线的斜率，再改变泊车半径，确定低约束段的泊车路径。利用车辆运动学模型，对车辆位置和姿态的分析，碰撞点到车辆的距离计算，证明了路径规划的可行性，生成的泊车轨迹比较符合泊车实际情况。

最短路径；变半径；路径规划

王龙

现就读于重庆交通大学车辆工程专业硕士，目前在清华大学汽车研究所实习，主要研究方向是自动泊车. 曾获得一项实用新型专利发明以及发表了一篇论文。

引言

自动泊车辅助系统可以在泊车时自主进行转向运动，驾驶员仅需控制油门、制动以及挂挡，并且该系统可以随时接管方向盘，停止系统作用。自动泊车辅助系统减轻了驾驶员的操作，给驾驶员泊车带来了第二种选择，近年来不断有外国的车型增添了这一功能。国内也不断有这方面的研究。

泊车的路径规划是自动泊车系统的重要一部分。当前的自动泊车规划主要是两圆弧相切型和两圆弧加一条斜直线型，且圆弧半径是泊车车辆的最小转弯半径。文献［1，2］中提出了基于最小转弯半径的两圆弧加直线的最短路径，并进行了最短路径的证明。文献［3］提出了基于多段圆弧和直线的平行泊车路径规划方法，依然没有摆脱最小转弯半径作为第二段的圆弧半径。文献［4］提出了改进的最小半径和不等半径两种几何路径规划方法，并对这两种方法进行了综合分析，得出两者的结合不仅可以大大扩大泊车起始区域的范围，但是没有提出具体的算法来规划路径。文献［5，6，7，8］分别利用贝尔样条曲线、回旋曲线、人机交互的模糊控制曲线来规划泊车路线，这些方法计算复杂且对系统的控制性要求高，不容易工程实现。本文通过对最短路径的研究，提出一个基于最短路径的变半径泊车路径，该路径规划易于理论推导且比较符合车辆实际泊车轨迹。

1　车辆泊车时运动学分析

首先对车辆进行简化，得到基本的尺寸模型，如图1为车辆的简化尺寸。并利用简化模型建立车辆泊车时的运动学模型。

从文献［1-7］中可以得到在低速情况下，泊车车体可以作为一个刚体，在不考虑侧偏的条件下，车辆的运动过程是由多段的圆弧组成。由于后轮与车身运动方向一致，后轮轨迹在车体运动过程中能够完全体现车体的运动轨迹，所以可以将后轮轴线中心坐标认为是车体运动坐标。可以用方向盘转角确定车辆的转弯半径，仅仅需要知道后轮轴线中心坐标的位置和车身偏角，就可以确定车辆的运动轨迹了。以此来建立模型。如图2所示，即为车辆运动学模型。

由图2所示，泊车车辆的位置可以用3个状态变量表示出来。这三个变量是后轴中心的坐标（x ，y）车辆正向时和水平方向的夹角θ，即车辆的航向角。v表示车辆前轴中心点的速度，表示车辆前轮φ

方向与车辆方向的夹角，l 表示泊车车辆的轴长。通过对车辆运动学的分析，可以列出车辆泊车时的运动方程：

2　基于最短路径的泊车路径规划

2.1最短路径分析

根据泊车路径要求可知，路径需要由导数连续的曲线构成，而在文献［1］中说明了由以车辆最小转弯半径为半径的圆弧和直线组成的路径为泊车的最短路径。若路径为圆和直线组成，则根据车辆的运动学的限制可知，路径的连接应由初始和终点的两段圆弧及与两段圆弧相切的直线组成，如图3所示。

如图3所示，车辆倒车过程可以描述为：车辆先以某一固定转弯半径向右侧转弯倒车，到达F1后，将方向盘回正，沿直线倒车到点F2后，将方向盘左打到某一固定角度后，逐渐将车身回正，当车身回正到与道路平行，且车辆M点到达理想停车点M'后，将方向盘回到原点即可完成此次倒车。

假设车辆到达理想泊车点时，以泊车车辆的后轴中心点建立坐标轴，如图3所示。车辆泊车起始点M到理想泊车点M'的水平距离为S。泊车车辆以圆心O1，半径R1转动一个角度θ所行驶的距离为S1，泊车车辆从F1到F2行驶的距离为L1，泊车车辆以圆心O2，半径R2转动一个角度θ所行驶的距离为S2，泊车从起点M到泊车到达理想停车点M'走过的总路程S是=SS0+。L从+S图3-1中的几何关系可以得到：

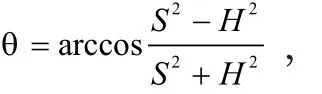
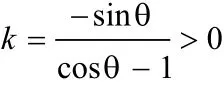
R1+R2和 S 成正比，随着 S 的增大而增大。

对R1+R2与 θ的关系进行分析，假设

对 f（ θ）进行求导，得到：

得到

将公式（2-4）带入得到

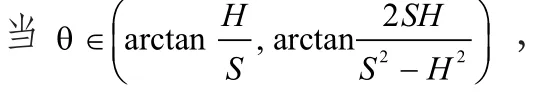
对 S0（θ）进行求导，得到S0'（θ）＞0，即随着转弯角度θ的增大，总路程不断增大。

根据随着转动角度θ的增大，两圆弧半径和R1+R2也不断增大的一一对应正比关系，得到随着两圆弧半径和R1+R2不断增大，转动角度θ也不断增大，总路程S0不断增大。当泊车起始时以最小转弯半径Rmin倒车和到达理想泊车点前一段圆弧也是以最小转弯半径Rmin进 行转弯的，此时 R1+R2最小且等于2Rmin，转动角度θ最小，总路程S0也最小。随着 R1+R2的不断增大，总路程S0也不断增大。故当车辆在起点与到达理想点前一段以最小转弯半径Rmin转弯时，泊车的总路程最短。

2.2高约束阶段路径分析与规划

用最小转弯半径进行的规划，对最小转弯半径要求比较高，即必须以最小转弯半径进行泊车，对车辆轮胎磨损严重。对泊车环境适应性差，实验过程中不成功的泊车次数比较多。对于这些问题，通过改变圆弧的半径克服这些缺点。

如图4所示，以泊车车辆的后轴中心点O作为参考点，泊车车辆在第二次转弯时车辆的避碰点为车辆前端的边缘点Q。此时车辆在转弯的过程中，车辆整体作为一个刚体，泊车车辆的前边缘点也在做着圆弧轨迹，此时车辆以后桥中心为基点做半径为R2的圆弧运动，泊车车辆的前边缘点Q做半径为R3的圆弧运动。LS为后轴中心点O到泊车车辆前段边缘点Q的直线距离。Lq为泊车车辆后轴中心到泊车车辆前端的直线距离。WL为泊车车辆的宽度。此时点O与点Q与点O2构成一个固定的三角形。其中θ3为两条直线LS与R2的夹角。Lh为泊车车辆后轴中心点O到泊车车辆后端的距离。D为泊车行使过程中的安全距离。Z为泊车过程中的障碍点。可以求得：

根据三角形的余弦公式得到：

当测量到车位长度大于一个值P1时，车辆只需要一次泊车。

为了保证泊车过程的平顺性和舒适性，选用一个合适的转弯半径R2，要求R2大于最小半径且满足多次泊车时的最大转弯半径。通过计算可以得到泊车结束时的位置，再根据转弯半径R2得到第二段圆弧的轨迹。在一次泊车的条件下，可以将第二段圆弧路径固化下来，转弯角度θ 不变化，这时可以确定第二段圆弧的起点F2。

2.3转动角度的分析

转动角度的取值应满足在H、S 的范围内，可以进行一次泊车，不发生碰撞。从实际泊车环境出发，转动角度的取值应尽量小，保证规划的路线尽可能短，同时转弯平顺。上边给出了转弯角度的大致范围，在最小取值内小中求大，即寻求最小取值范围内的最大值。假设第一段转弯半径R1大于等于R2，那么在转弯角度的范围内最小范围内只需要H最大，S最小，且满足规划路径的其他条件。利用公式2-4得到：

即转弯角度可以用下列式子求出：

假设直线段的表达式为y=a1x+b1。根据得到的 F2起点坐标和a1可以求得b1最终得到直线的表达式。可以计算直线段到障碍原点的距离 。其应满足以下条件：

2.4低约束阶段的分析与规划

当第二段转弯圆弧确定后，泊车规划路线的直线段与第二段圆弧的相切点F2可以确定，且直线的倾斜程度（即斜率）可以通过公式（2-17）求得。

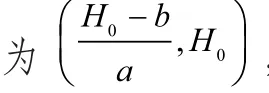
半径R2的圆弧与直线L1相切，圆心到直线的距离等于半径 。即：

得到：

最大转弯半径需要满足2个条件。

1. 泊车车辆后端在第一段圆弧泊车过程中不会撞住障碍点Z且保持一个安全距离D。

2. 最大转弯半径要与直线L1相切

用公式表示就是：

鉴于初始点的最大值Smax不容易求取，可以采用先求取满足直线段长度L1时的初始值S ，看是否符合最大转弯半径需要满足的初始点最大值Smax，若满足就选用此时的初始值S作为初始点的最大值；若未满足，可用此时的初始值S不断逼近初始点的最大值Smax，具体采用两点中值法，利用Smin作为下线，不断求取中值进行条件比较，若符合条件，继续进行中值比较，一直到找到最优解为止。

实际上只要起始点的位置大于Smin一个安全值即可，但是考虑到泊车车辆的舒适性和稳定性需要找到一个更合适的起始点。经过综合考虑将起点设为Smin与Smax的中点Smid。公式为：

这样做的好处是在保证舒适的泊车时，行驶的路线尽可能短。也可以增加驾驶舒适度的权重，将起始点设置在Smid与Smax之 间。但是没有一个具体的衡量标准，没法进行完全的量化，所以需要根据实验才可以更好的选择合适的起始点。

2.5多次泊车路线分析与规划

当测量的泊车位长度大于一次泊车的长度P1，需要进行多次泊车，如图6所示，对于多次泊车可以通过车辆较小的转弯半径不断走Z字型，最终走到Fn， 且此时车辆的航向角为零。通过MATLAB实验仿真获得泊车时到达检测停车位时候的点F3的坐标位置和半径R2。

假设在多次泊车时第一段圆弧的半径等于最大的第二段圆弧半径，通过公式2-15和2-17确定第二段圆弧的转弯角度θ，并得到第二段圆弧的圆心位置，最终规划出高约束阶段的二段泊车路径规划，然后进行低约束阶段的规划，最终获得多次泊车的路径规划。

3　实验仿真

3.1多次泊车的仿真数据

实验采用大众途安型号的车辆参数进行仿真，参数如下：车长4 395 mm，车宽为1 794 mm，前悬为880 mm，后悬为837 mm，车辆轮距为1 530 mm，轴距为2 678 mm，车辆行驶速度为km/h，最小转弯半径为5 600 mm，方向盘极限转角为540°。

通过MATLAB仿真可以得到多次泊车时入库时的半径R2与停车位长度Pl 的关系，如图7所示。仿真得到点F3的坐标位置，如图8所示：

3.2一次泊车路线及避碰区域仿真分析

H 的取值范围采用停车场的规范，H 的取值范围是（200，300），S的取值范围为测到停车位长度时通过障碍物后的直线距离（大概为130 cm）与泊车位长度之和，故一次泊车时S 的取值范围为（826，1 500）。根据公式（2-17）得到a1的值。

通过计算可以得到一次泊车时，R2=560 cm ，a1=0.5946 ，θ =30.2° ，D=20 cm 。在新坐标下，第二段圆弧的圆心O2=（-592.4， -470） ，第二段圆弧起点F2=（-319.2， 19.3），直线段的方程式为：

第一段圆弧需要的最小起始点位置与侧向距离有关，侧向距离越大，需要的最小起始点位置越小，当侧向距离H0=300 cm时，此时最小起始点位置为（140， 210），最大起始点位置为（450.54，210），此时，直线L1=100 cm，为最小距离。

通过计算的试验参数对其进行避障分析，得到如图9、10的黑色避障区域，主要由泊车规划运行第一个圆弧时的泊车后端运动的区域和运行第二个圆弧时泊车前端运动的区域组成。通过实验分析，发现可以很好的避开障碍物点Z且保持一个安全距离。

2.5多次泊车路线仿真及直线斜率计算

对于多次泊车规划的计算分析，在停车位长度大于656 cm时，如图11所示，通过拟合得到半径R与停车位长度Pl的关系式 ：

通过计算分析，并用MATLAB仿真得到此时半径R与直线斜率a 的关系，如图12所示。停车位长度Pl与斜率a 的关系，如图13所示：

通过检测到的停车位长度，可以通过公式3-3获得此时需要的斜率a 。

当停车位长度pl ≤656 cm时，为了保证车辆顺利泊车，此时S 的最小值定为786（656+130）cm。此时泊车车辆半径不断变化，取值范围R2=（460，480）。在此范围内半径R2与直线斜率a的关系如图14所示。半径R2与直线斜率a的关系公式：

通过计算和仿真分析，整个泊车过程不会发生碰撞。

4　结论

基于最短路径的泊车路径规划保证了在泊车路径较短的前提下，泊车需要的空间减小，泊车的舒适性增加，避免了泊车利用最小转弯半径进行泊车，汽车尽量做纯滚动运动。

通过实验仿真给出了多次泊车时停车位长度与直线斜率的拟合公式和第二段圆弧的半径与直线斜率的拟合公式，对其进行避碰计算，结果完全符合泊车的实际需要，证明了其方法的可行性。

［1］ Scheuer A， Fraichard T H， Planning Continuouscurvature Paths for Carlike Robots［C］， IEEE Transactions on Intelligent Robots and Systems， 1996：1304-1311.

［2］吕镇基.自动泊车轨迹规划算法研究及视觉平台结构设计［D］.哈尔滨工业大学，2012.

［3］杨妮娜，梁华为，王少平.平行泊车的路径规划方法及其仿真研究［J］.电子测量技术，2011，01：42-45.

［4］王道斌，梁华为，杨妮娜，高航.两种自主泊车路径规划方法的对比研究［J］.电子测量技术，2011，01：27-30+38.

［5］林蓁蓁，李庆，梁艳菊，陈大鹏.一种基于路径规划的自动平行泊车算法［J］.计算机应用研究，2012，05：1713-1715.

［6］宋金泽.自主泊车系统关键技术研究［D］.国防科学技术大学，2009.

［7］刘钰，马艳丽，李涛.基于Bezier曲线拟合的自主平行泊车轨迹模型仿真［J］. 科技导报，2011，11：59-61.

［8］黄迅.基于回旋曲线的自动平行泊车系统研究［D］.导师：曹立波.湖南大学，2014.

专家推荐

田哲文：

文章结构较为完整、有一定新意、研究的科学性好，有较强的实用性。

Variable Radius of Parking Path Planning based on Shortest Path

WANG Long1， ZHU Kai2
（1.College of mechanical and electrical engineering， Chongqing Jiaotong University . Chongqing404100，China； 2. College of engineering， China Agricultural University.Beijing 100083， China）

The automatic parking path planning belongs to from low to high constraints problems，also bound by a non-complete problem. Generally the path planning is not very desirable， for parking demanding conditions. According to resolve common problems from high to low constraint process，based on the shortest path， Firstly determine the parking path of parking vehicles enter the parking space in the highly constrained stage， calculate the length of parking spaces and the slope of the line fit formula to give a straight line slope， and then change parking radius of parking path in lower bound segment. Using the vehicle kinematic model， analysis of vehicle position and posture， calculate the distance of collision point to the vehicle to prove the feasibility of path planning， the generated parking trajectory more in line with the actual situation parking.

Shortest path； variable radius； path planning

N945.13

A

1005-2550（2015）06-0051-07

10.3969/j.issn.1005-2550.2015.05.010

2015-06-24