某型轻卡自激摆振多极限环特性研究★

张志龙，潘宁，陈长鹤，肖怀阳，魏道高

（1.合肥工业大学 机械与汽车工程学院，合肥 230009　2. 浙江吉利汽车研究院有限公司，　杭州 310052）

某型轻卡自激摆振多极限环特性研究★

张志龙1，潘宁1，陈长鹤1，肖怀阳2，魏道高1

（1.合肥工业大学 机械与汽车工程学院，合肥 2300092. 浙江吉利汽车研究院有限公司，杭州 310052）

汽车摆振与初始激励相关，足够大的初始激励才能激发大幅自激摆振即多极限环现象。为进一步研究汽车自激摆振多极限环现象，选用某型轻卡商用车作为样车，将悬架及转向系统干摩擦简化至主销处，选用迟滞环摩擦模型建立了整车十自由度摆振模型。运用数值方法，分析干摩擦力矩对摆振极限环的影响。结果表明，干摩擦幅值增加会使汽车摆振车速区间和摆振幅值减小，导致中间过渡单环区间消失。分析结果旨在为抑制该类型汽车振动提供理论参考。

转向轮摆振；干摩擦；多极限环；整车振动

张志龙

合肥工业大学车辆工程专业在读硕士研究生，研究方向为车辆系统动力学和非线性振动。

摆振是汽车常见的一种有害工况，汽车发生摆振时会引起转向盘和车身抖动，导致汽车操纵困难，加剧轮胎磨损，影响汽车的行驶安全性和乘坐舒适性。人们对汽车摆振的机理进行了长期广泛研究，并取得了丰硕成果［1-3］。

汽车摆振分为强迫摆振和自激摆振，强迫摆振是由轮胎失衡量等周期性干扰源产生，可通过对轮胎动平衡解决；而自激摆振是一种复杂的非线性振动，与转向系干摩擦、间隙等非线性因素相关，属于非线性动力学中的hopf分岔现象。Hopf分岔会产生稳定极限环和非稳定极限环，分别对应超临界分岔和亚临界分岔［4］。近年来许多学者从非线性角度对前轮自激摆振进行了研究：Karanam V.M.研究了前轮摆振对三轮汽车运动稳定性的影响［5］。李胜通过研究三自由前桥摆振发现迟滞环干摩擦会诱发多极限环振动［6］。王威分析了汽车转向系间隙诱导汽车摆振Hopf分岔特性［7］。蒋艮生考虑了轮胎定位参数对汽车摆振多极限环特性的影响［10］。

以上研究为解决汽车自激摆振问题提供了良好理论基础，但研究对象多局限于前桥摆振系统，不能全面反映摆振时的整车运动状态。本文针对以上不足，把研究对象扩展到包含转向盘、车桥和车身在内的整车十自由度摆振系统，选用迟滞环干摩擦模型，利用数值分析方法研究干摩擦诱发整车自激摆振产生的多极限环现象，以期丰富汽车自激摆振系统动力学内容。

1　整车十自由度摆振力学模型

文献［1］采用分析力学的方法建立了某载重汽车十四自由度摆振模型，分析了转向轮失衡量、轮胎定位参数对汽车摆振的影响，并研究了整车摆振和车辆操纵稳定性的关系。受当时条件限制，建模时没有考虑干摩擦和轮胎的非线性，主要研究了车辆的强迫摆振。本文在文献［1］的基础上，以整体式转向梯形和非独立悬架的国产某型轻卡为样车，考虑轮胎和干摩擦非线性，简化建立了整车摆振模型，其力学模型简图如图1所示。模型中包含了转向盘转角θs， 左、右轮绕其主销摆角θ1、θ2，左右梯形臂摆角θ3、θ4，前桥侧摆角φx，车身侧倾角ψ，前桥垂向跳动Z，整车侧向滑移Y、整车横摆角ω共10个自由度。在建模时假设车辆纵向速度V为常量。

整车摆振模型的运动微分方程如1.1节所示，轮胎力模型见1.2节，考虑了轮胎载荷转移，并选用精确度较高的魔术公式轮胎模型，干摩擦力矩见1.3节，选用迟滞环干摩擦模型。

1.1整车自激摆振系统微分方程

基于图1摆振力学简图，参考文献［1］摆振模型，考虑转向系干摩擦和轮胎非线性，运用拉格朗日方程，简化建立整车十自由度自激摆振微分方程如下：

1）方向盘绕转向管柱摆振方程

2）右前轮绕主销摆振方程

3） 左前轮绕主销摆振方程

4） 前桥绕纵轴线侧摆方程

5） 前桥垂直跳动方程

6） 整车侧向滑移方程

式中：Is为转向盘绕转向管柱转动惯量，Ic为左、右前轮总成绕主销的转动惯量，I1为转向轮总成绕与其旋转轴线垂直的质心主轴的转动惯量，Ik为转向轮总成绕其旋转轴线的转动惯量，Jqx为整个前桥总成绕其侧摆轴的转动惯量，Jx为悬置以上结构绕侧倾轴的转动惯量，Jz为整车绕 Z 轴的转动惯量，m1悬置以上机构的质量，m2为不包括转向轮总成的前桥质量，m3单个转向轮总成质量，m1q悬置以上结构分配在前桥质量，mq整个前桥质量，mzh为整车整备质量；

Fx1、Fx2分别为右、左前轮所受的纵向力，Fy1、Fy2分别为右、左前轮所受的侧向力，Fyr为右、左后轮所受的侧向力；

C1横拉杆当量阻尼系数，C2为转向梯形臂当量阻尼系数，Cξ为左、右前轮总成绕其主销的当量角阻尼系数，Cqt转向拉杆接头的当量阻尼系数，Cx1悬架减振器阻尼；

K1、K2为左、右转向梯形臂角刚度，K2d为转向节臂角刚度，Kf为转向器与转向盘之间的当量连接角刚度，K11为前钢板弹簧垂直，K22为后钢板弹簧垂直刚度；Kh为 横拉杆线刚度，Kcz为轮胎垂直刚度，Kp为 轮胎侧偏刚度；KC为轮胎侧向刚度；

f 为轮胎滚动阻力系数，g 为重力加速度，α主销后倾角， γ 主销内倾角，ε 汽车静平衡时的车轮外倾角，λ 车轮前束角，R 为车轮滚动半径，β为轮胎拖距，L 为前轮质心至主销距离，B为前轮距，Bq、Bh前后悬架板簧距，h1悬置以上结构质心距侧倾轴的距离，h2前桥质心距其侧摆轴的距离，i0为方向机速比。

1.2轮胎力学模型

（1）轮胎垂直载荷模型

根据轮胎径向变形时弹性势能的变化，推导可得转向系统摆振时右、左前轮受到的地面垂直作用力：

式中，Kcz为轮胎的垂直刚度。

（2）轮胎侧向力模型

摆振方程轮胎侧向力选用魔术公式模型［11］：

式中，ai（i=1，2，r分别表示左前轮、右前轮、后轮）表示为左右前轮及后轮侧偏角，Bi、Ci、Di、Ei分别称为公式中的刚度因子、形状因子、峰值因子、 曲率因子，a1、a2、a3、a4、a5、a6、a7、a8为由试验拟合得到的参数。其数值如表1所示：

由式（12）及表1计算得近似静平衡状态下的前后轮轮胎侧偏力与侧偏角关系曲线如图2所示：

表1　轮胎拟合参数

本文实际计算时，前轮的侧偏角要考虑到摆振的影响，运用张弦理论，考虑轮胎侧向变形松弛长度的影响，建立前轮轮胎滚动的非完整约束方程：

式中：α为轮胎印记半长度，σ为轮胎松弛长度，V为纵向车速。而后轮的侧偏角由整车的运动状态决定：

式中：b为整车质心距后桥距离。

1.3干摩擦力矩模型

相互接触的两部件间的摩擦，在其相对速度近似为零时，会产生粘滞特性。因此，引入考虑了此粘滞特性的迟滞环模型［5］（如图5所示），表示转向柱与车架总成间的干摩擦力矩。

由图3可得

其中Mc为 干摩擦力矩迟滞环模型的幅值，1为角速度上界值。

2.汽车自激摆振系统数值计算与分析

2.1摆振系统分岔特性计算与分析

基于前述建立的摆振系统微分方程式，建立了Simulink仿真模型，运用四阶Runge-Kutta法进行数值求解，计算所需的主要汽车参数见表2：

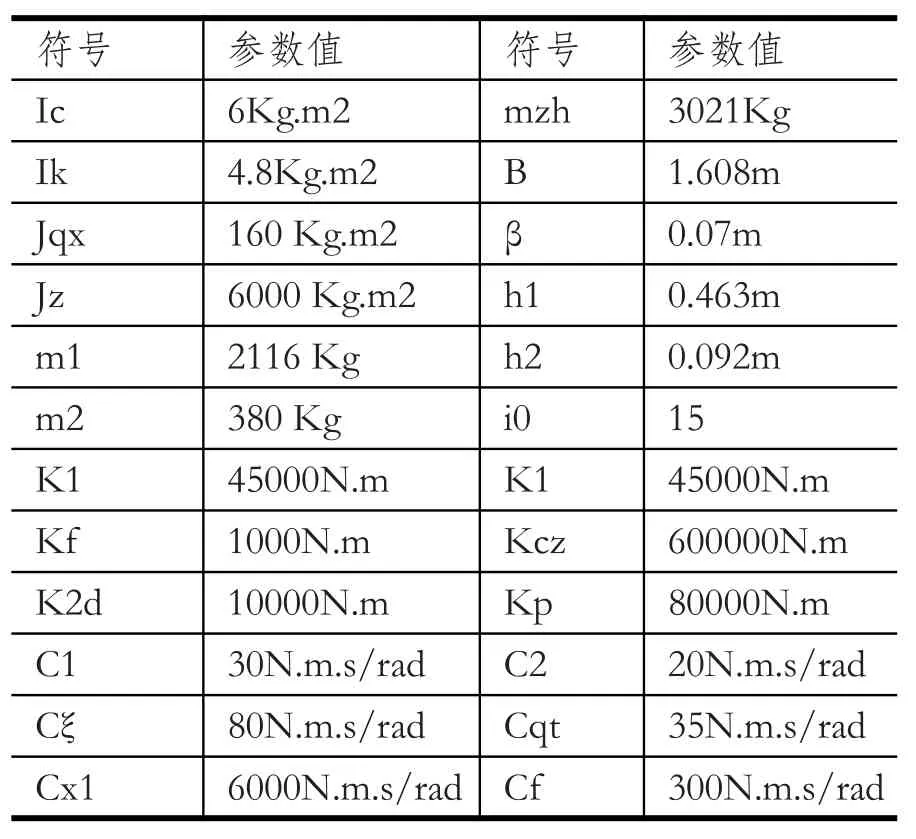
表2　计算所需主要参数

考虑悬架与转向机构运动副干摩擦对整车自激摆振多极限环特性影响，分别取主销处干摩擦力矩为15N.m、30N.m，研究整车十自由度动力学系统自激摆振现象，以车辆前进速度V为分岔参数，分别取前轮转角初始激励为0.5°和5°，进行分岔特性数值计算，获得右前轮摆角θ1、前桥侧摆φx和车身侧倾角ψ随车速V的hopf分岔特性图，见图4：

表3　不同Mc各自由度随车速的摆振区间及摆角峰值

参照图4：各自由度整体横向对比，整车的各个自由度摆振在同一干摩擦力矩下分岔的速度区间一致，幅值变化趋势相同，说明前桥摆振引起的整车多个自由度方向的振动具有动力学上的一致性；

单就某一自由度例如右前轮转角θ1而言，随着干摩擦力矩的增加，各个自由度振动的幅值减小，其中第一临界摆振车速提高，第二临界车速降低，因而整个大幅摆振区间减小；

从极限环区间来看，在考虑迟滞环干摩擦模型后，整车摆振系统中出现了不稳定的极限环，从而出现了多环区间，且随着干摩擦力矩增加多环区间也随之加大，单环区间逐渐减小直至消失，在整个摆振区间内全部出现了多环。

2.2整车摆振系统多极限环特性

从摆振速度分岔图4（a）和表3可知Mc=15N.m时右前轮摆振第一多环区间为28.8Km/h～41.4Km/h。为了进一步分析多极限环自激振动特性，取分岔图4（a）中Mc=15N.m，V=35Km/h处进行时域和频域的分析：在这一条件下分别施加0.5°、2.5°和 4.5°、10°初始激励，右前轮转角θ1对应的摆振时域图、相图和频谱图分别如图5、图6所示：

表4　第一临界车速附近右轮摆角多极限环幅值

图5为右前轮摆角在不同初始激励下的摆角时域图，0.5°和2.5°初始激励时，右轮摆角幅值最终都为1.5°；而当初始激励为4.5°和10°时，右轮摆角幅值最终都为7.5°，说明存在幅值为1.5°和7.5°的两个稳定极限环，在两个稳定极限环之间必定存在一个不稳定极限环［6］，对初始激励从2.5°到4.5°进行逐步搜索，得到不稳定极限环幅值在3.7°附近；如图7（a）所示，当初始激励θ0 ＜3.7°时，系统发生幅值较小的自激振动，右前轮摆振最终趋于小稳定极限环，其幅值为1.5°；当初始激励θ0 ＞ 3.7°时，系统发生幅值较大的自激振动，右前轮摆振最终趋于大稳定极限环，其幅值为7.5°。

图6为大稳定极限环和小稳定极限环的相图和频谱图对比：图6（a）与图6（b）比较可得，大稳定极限环和小稳定极限环的频率均为4Hz左右，说明出现多极限环自激振动时，摆振的频率与初始激励和摆振幅值无关。

图7为干摩擦幅值Mc取15N.m，汽车车速V分别为35Km/h、38Km/h和41Km/h时右前轮摆振的多极限环相图，从图中可以看出随着车速V缓慢增加，小极限环幅值A1几乎不变，大极限环幅值A2逐渐增加，不稳定极限环幅值A3逐渐减小，当A3减小至A1时，系统不再出现不稳定极限环，说明在Mc=15N.m，V=41Km/h时，小初始激励也会产生与大初始激励相同的大幅自激摆振现象，危害汽车行驶安全。由图4 Mc=30N.m下的右前轮摆振分岔图可知，增加干摩擦可以消除小初始激励产生大幅自激摆振现象，从而增加汽车行驶的抗干扰能力。

3　结 论

（1）选用魔术公式轮胎模型和迟滞环干摩擦模型，参考文献［1］建立了包含方向盘摆动、前桥侧摆、垂直跳动，整车侧滑、侧倾、横摆的某商用车整车十自由度自激振动模型。

（2）运用数值方法找到转向轮摆振引发的整车自激振动多极限环现象，对整车各个自由度的摆振速度分岔特性研究表明，相同参数时，整车的各个方向振动速度分岔区间相同，前轮摆振会引起汽车车身整体的振动。

（3）干摩擦幅值增加会使整车摆振区间减小，幅值降低，在初始激励较小时不产生危害严重的大幅自激摆振现象，但过度增加系统干摩擦会影响汽车转向轻便性，因而要综合考虑减小系统摆振和整车操纵稳定性的要求来匹配转向系统干摩擦。

［1］宋健. 导向轮轮胎和定位参数对汽车摆振影响的研究及整车横向动力学优化分析 ［D］. 北京： 清华大学， 1989.

［2］王鹏，魏道高，潘之杰，肖怀阳. 转向柱后倾角对三轮汽车前轮自激摆振特性影响［J］. 汽车科技，2014， 1： 5-10.

［3］韩同群，邹汉华.越野汽车前轮摆振影响因素仿真［J］.农业机械学报，2007，38（5）：27～31，26.

［4］陆启韶.分岔与奇异性［M］.上海：上海科学教育出版社，1995.

［5］Karanam V.M.， Ghosal A. Studies on the wobble mode stability of a three-wheeled vehicle［J］. Proceedings of the Institution of Mechanical Engineers， Part D：Journal of Automobile Engineering， 2013， 227（8）：1200-1209.

［6］李胜.分岔理论在汽车转向轮摆振机理及其控制策略研究中的应用［D］.长春：吉林大学，2005.

［7］王威，宋玉玲，李瑰贤. 独立悬架汽车转向系间隙与干摩擦对其Hopf分岔特性的影响［J］. 机械工程学报，2011，47（2）：130-135.

［8］贺丽娟，林逸. 汽车操纵稳定性与前轮摆振的非线性仿真分析［J］. 汽车工程，2007，19（5）：389-392.

［9］杨秀建，李西涛.半挂汽车列车操纵特性与横向稳定性的研究［J］. 汽车工程，2012，34（12）：1107-1113.

［10］魏道高，蒋艮生. 主销后倾角对独立悬架汽车自激摆振极限环特性的影响［J］. 农业机械学报，2012，43（12）：5-10.

［11］Pacejka H. Tyre and vehicle dynamics［M］. Elsevier，2005.

专家推荐

田哲文：

文章建立了整车十自由度摆振力学模型，运用数值方法找到转向轮摆振引发的整车自激振动多极限环现象，内容详实，论证较为充分，具有一定的学术性，但在细节处理方面还需加强。

Study of the Effects upon Vehicle Stability Exerted by Tie Rod End Clearances under Slalom Maneuver

ZHANG Zhi-long1， PAN Ning1， CHEN Chang-he1， XIAO Huai-yang2， WEI Dao-gao1
（1. School of Mechanical and Automotive Engineering， Hefei University of Technology； 2. Zhejiang Geely Automobile Institute）

The shimmy of vehicle is related with initial excitation. Intense external excitations may present sharp fluctuation as multiple limit cycles responses. In order to research on multiple limit cycles，a light truck shimmy model including hysteresis loop friction is established and numerical calculation is performed to study the influence of dry friction on limit cycles. The results show that when increase the dry friction torque， both the shimmy range and vibration amplitude are gradually reduced. This analysis results may provide theoretical reference to automobile vibration study.

Wheel Shimmy； Dry Friction； Multiple Limit Cycles； Vehicle Vibration

U464.21

A

1005-2550（2015）04-0001-06

10.3969/j.issn.1005-2550.2015.04.001

2015-01-20

国家自然科学基金项目（51375130）；吉利汽车研究院浙江省汽车安全技术重点实验室开放基金项目（2009E10013）。