基于Taguchi方法的带筋注塑件翘曲变形研究

徐小青，孙庆东，尹 晨

(扬州职业大学，江苏扬州 225009)

塑料件比金属件的弹性模量低得多，因此，在设计需承受载荷的塑料制品时，一般在注塑件上通过设计加强筋、折弯和曲面等方法来增加制品的强度和刚度，而其中通过设计加强筋的方法最为实用和可靠［1］。在设计加强筋时，大多数工程师只注重加强筋厚度、高度和数量，很少考虑加强筋的不同截面形状和位置角度。本文主要研究不同截面形状和位置角度的筋对PC/ABS、POM和PA66注塑件翘曲变形的影响，为筋的正确设计提供参考。

1 筋的设计

1.1 加强筋的设计

为了更方便地系统研究加强筋对注塑件翘曲变形的影响，设计了截面面积A和高度a相等，但横截面形状不同的三角形、梯形和矩形的加强筋，见图1。截面A==(c+d)=ae。

同时还设计了与X方向成0°、45°和90°夹角的三种位置角度的加强筋，见图2。

图1 筋的截面形状

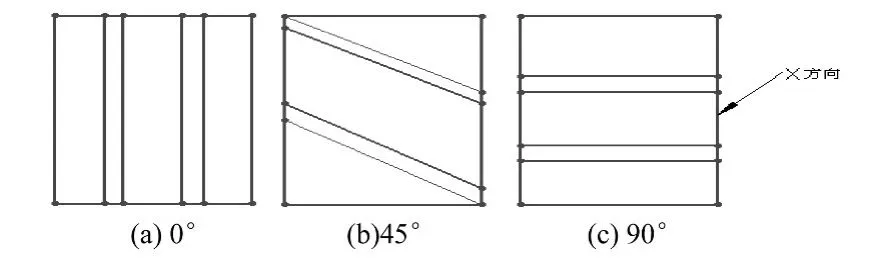
图2 筋的位置角度

1.2 加强筋的试验模型

图3(a)显示了没有设计加强筋的模型，并且定义了X、Y和Z方向。图3(b)显示了带有网格和加强筋的一种分析模型。

图3 试验制品模型

通过Solidworks设计不同的分析模型，然后生产STL文件，导入到MPI模块中。采用Fusion进行网格划分，有限元分析模型数据为:三角形单元数=2888，节点数=1446，匹配率为97.2%。

2 试验设计

2.1 试验材料

选用的牌号为:Multilon T－3011 TG5667的高分子 PC/ABS材料，类型为 Amorphous;Hostaform C 9021的高分子POM材料，类型为Crystalline;Celstran PA66－GF50－02的高分子PA66材料，类型为Crystalline。

2.2 Taguchi试验设计

按照Taguchi方法，对PC/ABS、POM和PA66三种注塑件分别按照五因素三水平进行L18正交实验矩阵设计［2，3］，相应的实验水平和因子见表1－表3。

表1 PC/ABS材料试验的水平和因子

模具温度(X1)/℃60 75 90熔体温度(X2)/℃ 245 265 285注射时间(X3)/s 1.0 1.4 1.8筋的形状(X4) a b c筋的角度(X5)/°0 45 90

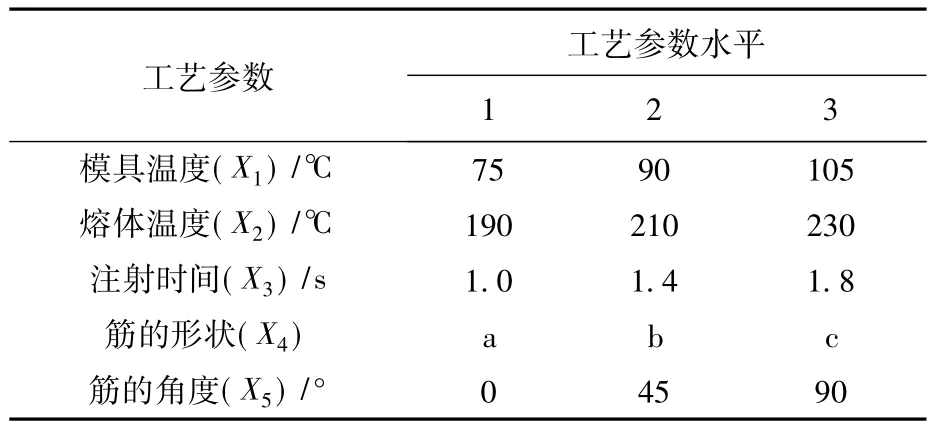
表2 POM材料试验的水平和因子

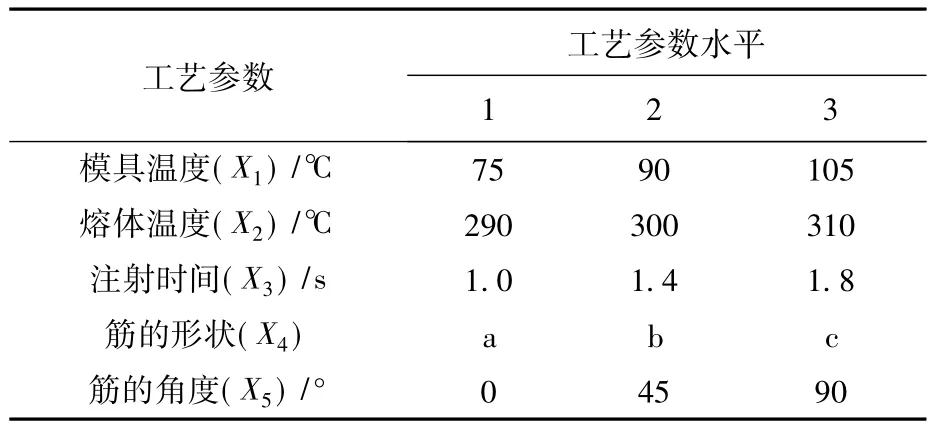
表3 PA66材料试验的水平和因子

3 结果分析

3.1 基于最小翘曲值的最优工艺参数组合

为了能得到最小翘曲变形，将采用信噪比函数来计算翘曲反应值，它主要用于质量性能目标值越小越好情况，其信噪比的表达式为:

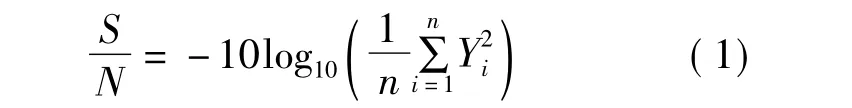
根据翘曲试验结果，利用信噪比函数来进行计算并对此进行分析，分析结果见图4－图6。

图4 PC/ABS制品信噪比结果分析

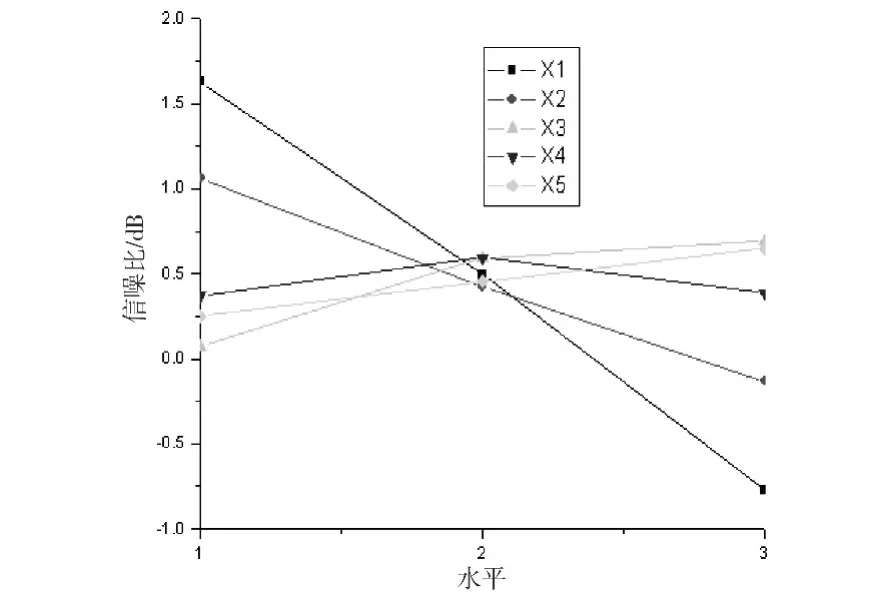
图5 POM制品信噪比结果分析

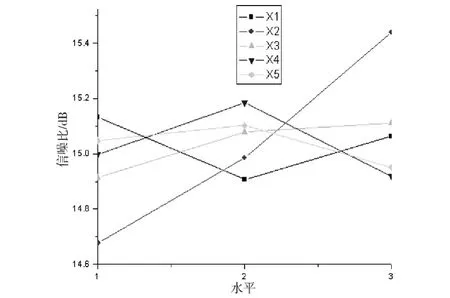
图6 PA66制品信噪比结果分析

信噪比函数值越大，可知其表示翘曲值越小。从图4－图6分别可知，PC/ABS制品和POM制品的最大的信噪比组合为X11X21X33X42X53，即模具温度60℃，熔体温度245℃，注射时间为1.8s，筋的形状为梯形，筋的角度与X方向成90°，为最佳工艺参数组合;PA66制品最大的信噪比组合为X11X23X33X42X52，即模具温度60℃，熔体温度285℃，注射时间为1.8s，筋的形状为梯形，筋的角度与X方向成45°，为最佳工艺参数组合。

3.2 工艺参数对翘曲影响程度分析

利用ANOVA方法来分析各个工艺参数对翘曲变形的影响程度［4，5］。

针对PC/ABS、POM和PA66材料，下列工艺参数对翘曲变形的影响程度分别为，模具温度:20.36%、73.5%和 6.9%;熔体温度:10.52%、18.1%和 75%;注射时间:50.22%、5.5%和5.6%;筋的形状:8.5%、0.8%和9.5%;筋的角度:10.4%、2.1%和3%。

筋的形状和角度对翘曲变形有着很大的影响，尤其是PC/ABS和PA66注塑件。

3.3 结果预测与试验验证

依据上述分析结果以及优化组合，可以预测出最小翘曲值，见表4。

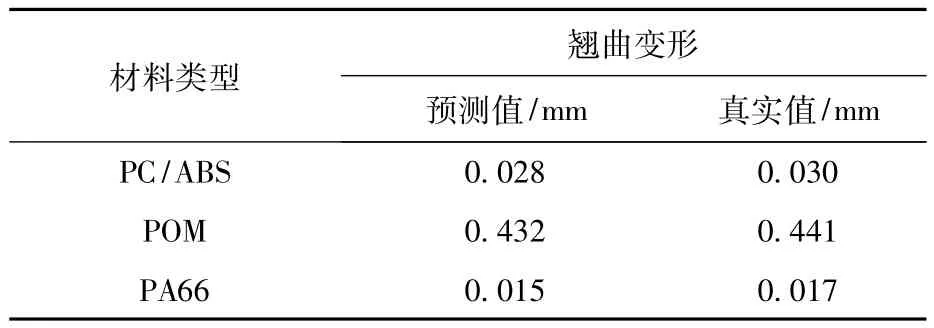
表4 翘曲预测与真实值

采用优化工艺参数组合进行试验，得到了试验的最小翘曲值。PC/ABS、POM和PA66注塑制品翘曲值误差分别为6.7%、2%和11.8%，考虑软件模拟分析误差，此误差值在可接受范围内。

4 结论

利用Taguchi方法能够得到了工艺参数的优化组合及预测最小翘曲值。针对PC/ABS和POM带筋注塑件，采用与X方向成90°夹角的梯形截面的加强筋，能得到最小的翘曲值;针对PA66注塑件，采用与X方向成45°夹角的梯形截面的加强筋，能得到最小的翘曲值;针对不同的材料类型，加强筋对制品翘曲的影响程度不尽相同，所以在设计加强筋时应该加以考虑。研究结果为以后的塑料件加强筋的设计提供科学指导。

［1］屈华昌.塑料成型工艺与模具设计［M］.北京:机械工业出版社，2004.

［2］OZCELIK B，ERZURUMLU T.Comparison of the warpage optimization in the plastic injection molding using ANOVA，neural network model and genetic algorithm［J］.Journal of Materials Processing Technology，2006(171):437－445.

［3］PEACE G S.Taguchi Methods:A Hands－ On Approach［M］.New York:Addison － Wesley，1993.

［4］PHADKE M S.Quality Engineering Using Robust Design［M］.New Jersey:Prentice － hall，1989.

［5］ERZURUMLU T，OZCELIK B.Minimization of warpage and sink index in injection－molded thermoplastic parts using Taguchi optimization method［J］.Materials and design，2006(27):853 －861.