基于midas的地下车库无梁楼盖结构的配筋计算研究

万志强

（广东省建筑设计研究院　广东　广州　510010）

基于midas的地下车库无梁楼盖结构的配筋计算研究

万志强

（广东省建筑设计研究院广东广州510010）

无梁楼盖如今已广泛应用于商业地产等各类民用建筑，本文立足于实际工程应用，运用midas分析无梁楼盖的弯矩分布，并对无梁楼盖的近似计算方法进行分析比较，同时控制地下室顶板裂缝值，从而得出无梁楼盖的板配筋结果，对结构设计人员的无梁楼盖施工图设计有一定的参考意义。

无梁楼盖；配筋值；施工图；midas

1　引言

随着城市人口的不断增长，开发地下空间为未来建筑发展的趋势，如商业建筑的多层地下室、生活小区的地下车库等。地下车库由于建设成本的限制，导致地下车库层高受限，采用无梁楼盖是增加楼层使用空间高度的最有效方法，其是一种双向受力楼板，板内钢筋沿两个方向布置，传力途径明确，因而无梁楼盖结构广泛应用于地下室的结构设计中。

2　无梁楼盖结构体系受力特点及计算方法

2.1无梁楼盖结构受力特点

无梁楼盖是由楼板、柱和柱帽组成的板柱结构体系，楼面荷载直接由板柱传给柱及柱下基础。因此其缩短了传力路径，增大了楼层净空，并且节约了施工模板，但楼板较厚，楼盖材料用量较多，楼盖的抗弯刚度较小，柱子周边的剪应力集中，可能会引起板的冲切破坏，同时在计算地震作用时，无梁楼盖体系中的板柱节点将产生不平衡弯矩，不平衡弯矩的反复作用将严重影响节点的承载力，无梁楼盖体系中板柱节点是抗冲切和抗震的薄弱环节，节点的破坏是导致结构倒塌的主要原因，因此，板柱体系抗震性能较差，主要用于承受竖向荷载作用。

2.2无梁楼盖结构的计算方法

无梁楼盖结构在竖向荷载作用下的内力及位移计算，通常用经验系数法、等代框架法和有限元法。

（1）经验系数法

经验系数法在实践经验基础上给出了两个方向截面总弯矩的分配系数，再将截面总弯矩分配给柱上板带和跨中板带，并按分配的弯矩计算各自的配筋。这是三种方法中最直接的计算方法，可以不借助任何计算工具而直接手算，因而受到广大设计人员欢迎。但该法只适用于规则结构，否则会出现较大误差，图1表示板带划分区域。

（2）等代框架法

等代框架法将无梁楼盖结构沿纵向和横向柱列划分为两个方向的等代框架梁，框架梁的高度取板厚，在竖向荷载的作用下，等代框架梁的宽度取为板跨中心线间的距离，计算中纵横两方向均应承担全部荷载，用空间分析程序一次计算，即可得出结构板的内力。按等代框架计算垂直荷载作用下板的弯矩，当平板与密肋板的任一区域的长短边长比小于2时，可分配给柱上板带和跨中板带支座负弯矩分别为75％和24％，跨中正弯矩分别为55％和45％；有柱帽时，其支座负弯矩应取刚域边缘处的值，除边支座弯矩和边跨中弯矩外，分配到各板带上的弯矩均应乘以0.8的系数。

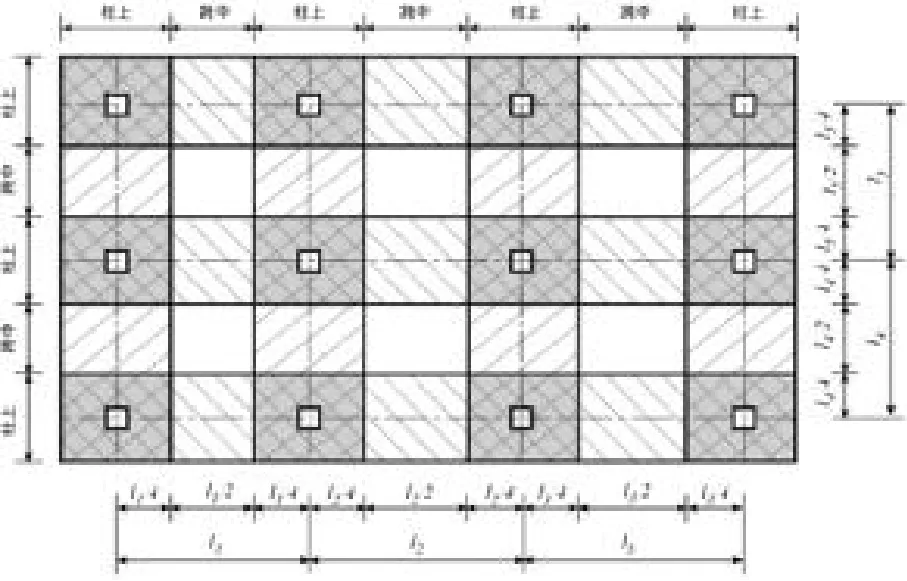
图1　板带划分

（3）有限元法

有限元法将无梁楼盖划分为若干板壳单元，用有限元程序进行求解，其基本原理，将楼板划分成若干板带，并在板带上设置若干剖面，利用有限元分析结果积分计算剖面总内力，形成设计截面，并根据现行规范的规定进行楼板正截面应力验算和受弯承载力配筋设计。

经验系数方法简单易行，但适用条件较为苛刻，实际应用面较小，等代框架法超越了经验系数法的适用条件限制，并且考虑了柱和楼盖间的相互影响，但是，等代框架法毕竟是建立在经验之上的简化计算方法，存在一些不足之处。而有限元法计算无梁楼盖没有柱上和跨中板带的划分，在一定程度上是一种精确计算楼盖平面各点内力和配筋的方法。因此，本文基于有限元计算方法，分析地下室车库的无梁楼板配筋。

3　基于midas有限元计算模型的建立

3.1无梁楼盖结构midas的模型建立

本文依据工程实例，建立midas分析模型。某工程位于广东省某市，为一大型地下停车场，地下室3层，地上总面积为34575m2地下建筑面积为8897m2，负一层～负三层层高分别为3.6m、3.4m、3.4m，其中负一层负二层为停车场，采用无梁楼盖结构，厚300mm，底板为400mm。梁板柱墙都使用C30混凝土，钢筋为HRB400。该工程用midas Gen软件整体建模分析，模型如图2所示。模型中的楼板采用板单元，厚度为300mm，柱帽厚度为800mm，楼板和柱帽均为板单元，板单元分割网格尺寸为500mm×500mm，框架柱为线单元，尺寸为600mm×600mm，边梁为线单元，尺寸为300mm×600mm。无梁楼盖四周与剪力墙连接，剪力墙为平面墙单元，框架柱和剪力墙底端边界条件均设置为固定端，恒载取16kN/m2，活载取5kN/m2（如图3）。

图2　车库无梁楼盖midas模型

图3　midas网格划分

3.2无梁楼盖有限元计算结果及分析

由于楼板按照裂缝控制配筋，因此在有限元计算结构体系后，按照恒载和活载的标准组合，得出的结果如图4。

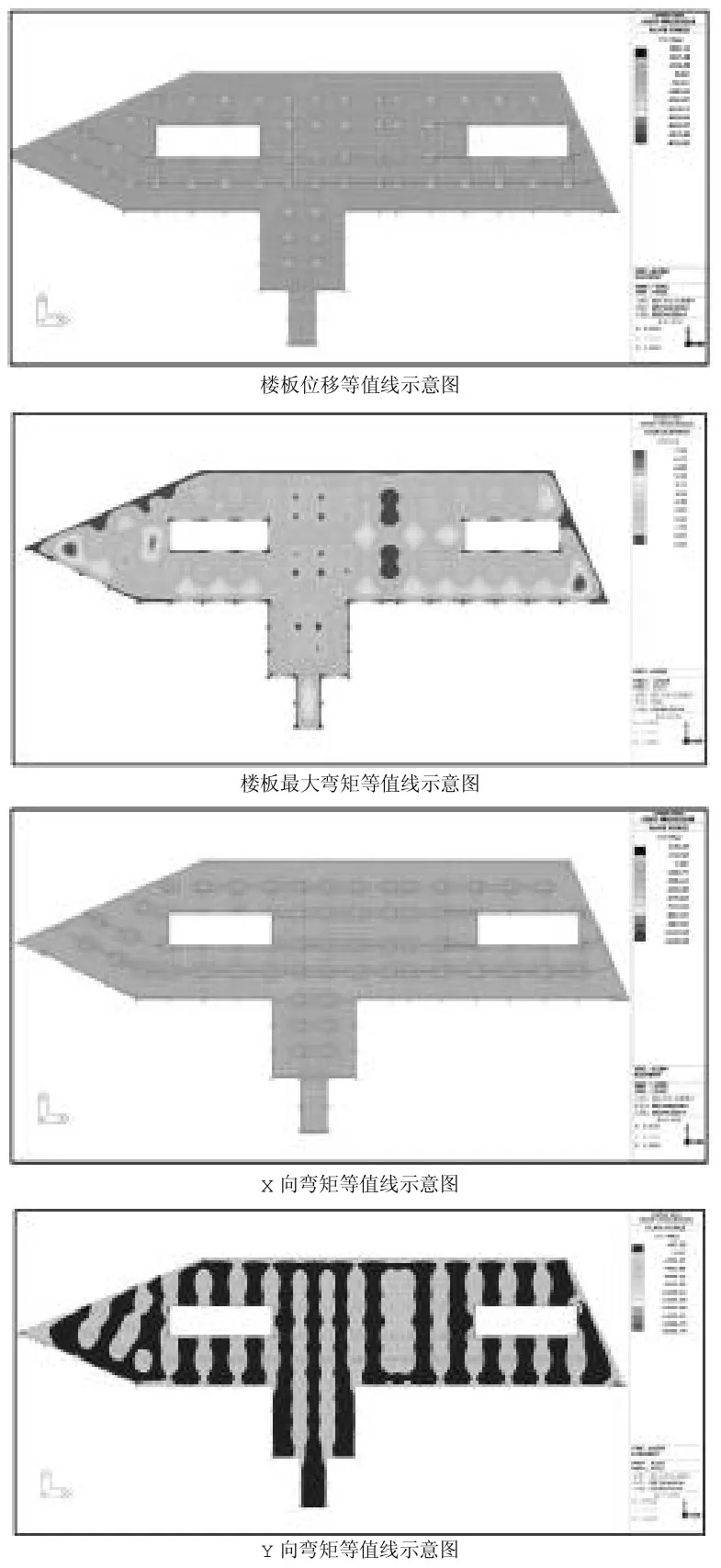
图4　无梁楼盖的弯矩和位移图

4　基于midas有限元计算的配筋结果

通过进行有限元单元分析，显示板跨中最大弯矩值和柱帽顶面最小弯矩值，如图4所示。板跨中最大弯矩值Mxx=58kN·m，Myy=100kN· m；柱帽最小弯矩值Mxx=-250kN·m，Myy=-350kN·m，按照裂缝计算配筋，采用理正结构设计软件6.5计算配筋，计算结果如下：

（1）截面有效高度：

（2）受拉钢筋应力计算，根据《混凝土规范》式7.1.4-3：

（3）按有效受拉混凝土截面面积计算的纵向受拉钢筋配筋率，根据《混凝土规范》式7.1.2-4：

（4）裂缝间纵向受拉钢筋应变不均匀系数，根据《混凝土规范》式7.1.2-2：受拉区纵向钢筋的等效直径deq：

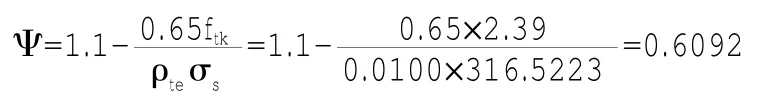
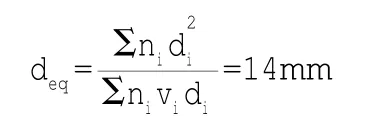
根据《混凝土规范》表7.1.2-1构件受力特征系数αcr=1.9：（5）最大裂缝宽度计算，根据《混凝土规范》式7.1.2-1：

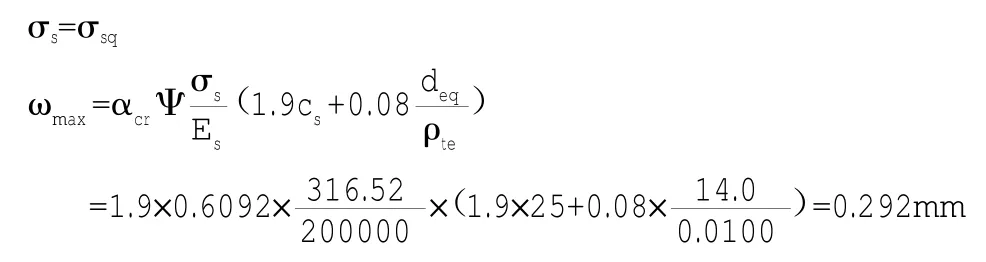
验算最大裂缝宽度：0.292（mm）＜[ωmax]=0.300（mm），因此需要钢筋为直径14@150加上12@150的，配筋面积为1780mm2满足裂缝值为0.3mm的要求。

5　结论

（1）探讨了基于midas有限元分析软件计算无梁楼盖的板弯矩分析方法，同时运用理正计算软件，深入研究了板的配筋计算方法。

（2）本文分别介绍了计算无梁楼盖的计算方法优点及不足，以及在实际运用中各种方法的缺陷，重点分析了midas有限元软件在计算无梁楼盖板弯矩的优点。

（3）通过对无梁楼盖板弯矩研究，体现了有限元计算方法的实用性及准确性，同时在无梁楼盖钢筋的配置方式，更加简单、有效，对设计人员有一定的指导意义。

[1]李俊兰，吕西林，周德源.地震作用下板柱结构等代框架法计算模型的研究.建筑结构学报，1999.

[2]郑文忠，王英.后张预应力混凝土平板柱结构设计与工程实例.黑龙江科学技术出版社，1999.

[3]王祖华，等.混凝土与砌体结构.华南理工大学出版社，1992.

[4]朱聘儒，编著.双向板无梁楼盖.中国建筑工业出版社，1999.

X43

A

1673-0038（2015）22-0015-02

2015-3-15

万志强（1987-），男，广东广州人，硕士研究生，主要从事建筑结构设计方面的工作。