基于遗传算法的柔性机器人制造单元调度问题研究*
2015-10-31龙传泽杨煜俊
龙传泽,杨煜俊
(广东工业大学 机电工程学院 广东省计算机集成制造重点实验室,广州 510006)
基于遗传算法的柔性机器人制造单元调度问题研究*
龙传泽,杨煜俊
(广东工业大学 机电工程学院 广东省计算机集成制造重点实验室,广州510006)
考虑机器人在装载站、机床、卸载站三者间搬运时间和空载时间的情况下求解柔性机器人制造单元Job-shop类型调度问题,目标是求所有工件加工完成并搬至卸载站的最短时间。首先,在分析机器人制造单元调度问题特点的基础上建立其数学模型,提出了一种新的对机器人搬运工序排序组成搬运序列矩阵的调度方法,机器人按搬运序列搬运,机床则按先到先服务规则(FCFS)加工;然后针对这种调度方法提出了一种改进遗传算法,为遗传算法设计了一种基于搬运工序编码方法与启发式分配策略,设计了一种启发式搬运矩阵调整方法,最后,把启发式调整算法与遗传算法结合组成混合算法对调度问题进行求解,通过标准算例计算,验证了算法的有效性。
机器人制造单元;Job-Shop;混合遗传算法
0 引言
计算机集成制造技术的发展使社会生产方式发生了深刻的变革,以工业机器人为核心的智能制造技术开始应用于企业生产。柔性机器人制造单元就是在这样背景下产生的一个由控制系统、机器人物料运输系统、机床等组成的智能制造系统。智能制造是制造业发展的方向,目前国内对柔性制造单元系统调度问题的研究较少,因此开展对柔性机器人制造单元的调度问题深入研究有重的意义,文献[1]对用遗传算法解决Job-shop问题进行了阐述,文献[2]设计了一种考虑工序相关性的动态Job-shop调度问题启发式算法,文献[3]使用一种新的编码方法设计了两种解决经典Job-shop类型车间作业问题的粒子群算法,以上文献在求解传统Job-shop类型车间调度问题上得到了较好的结果,然而都忽略了搬运时间。文献[4]构造一个新的领域结构,使用改进禁忌搜索算法解决带单台搬运机器人Job-shop类型车间调度问题,但没有考虑多台搬运设备的情况。文献[5]提出一种新的混合整数规划模型,通过限制同时加工的最大工件数,解决带一台搬运设备的有限缓存区容量柔性制造系统调度问题,但限制最大工件数将降低生产效率。文献[6-7]改进析取图模型,使用三向量方法通过关键路径上关键块的移动构造搜索领域解决带多台搬运机器人Job-shop类型车间调度问题,却没有考虑工件从装载站搬入和卸载站搬出的过程。文献[8]研究柔性车间作业调度问题,使用机器负荷平衡的启发式规则分配机器,提出改进混合遗传算法,解决了单目标和多目标柔性作业单元调度问题,但也没有考虑搬运时间,文献[9]使用不同的进化算法较好的解决了由AGV小车和机床组成的柔性制造系统调度问题,但忽略了最后一道工序加工完成后到卸载站的搬运工序。
本文提出了一种对各台机器人搬运工序排序组成搬运序列矩阵,机床按搬运序列搬运,机床则按先到先服务的规则(FCFS)加工的调度方法,并提出针对这种调度方法的混合遗传算法,较好的解决了多机器人柔性制造单元Job-shop类型调度问题。
1 问题描述
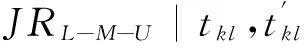
2 数学模型
2.1参数定义
J:工件集合J={J1,…,Jn};
R:机器人集合R={R1,…,Rr};
M:设备集合M={M0,…,Mm+1},其中M0为装载站,Mm+1为卸载站,{M1,…,Mm}为机床;
Ij:工件J的加工工序集合Ij={oj1,…,oji};
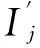
oji: 工件j的第i道加工工序;
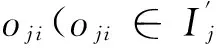
pji: 工序oji(oji∈Ij)的加工时间;
tr(Mm1,Mm2): 设备Mm1与设备Mm2间的搬运时间;
tr′(Mm1,Mm2): 设备Mm1与设备Mm2间的空载时间;
S(toji): 搬运工序toji的开始时间;
C(toji): 搬运工序toji的完成时间;
S(oji): 加工工序oji的开始时间;
C(oji): 加工工序oji的完成时间;
R(toji): 给搬运工序toji分配的机器人,R(toji)∈R;
Seq(Rr): 机器人Rr的搬运序列;
Seq(R): 机器人搬运序列矩阵,由Seq(Rr)组成;
Y(toji):toji在机器人R(toji)搬运序列中的序号;
Cj: 工件j到达卸载站时间。
2.2目标函数与约束条件
目标函数:
约束条件:
(1)首道加工工序时间约束,工件需从装载站搬到其首道工序加工机床:
S(oj1)≥tr(M0,μj1),∀Jj∈J
(2)机器人搬运序列中相临两道搬运任务时间约束,一台机器人完成其上道搬运任务,空载到其下一道搬运任务的初始机床,再将工件搬运到其加工机床:
S(toj2i2)≥C(toj1i1)+tr′(μj1i1,μj2(i2-1))+tr(μj2(i2-1),μj2i2)
R(toj2i2)=R(toj1i1),
Y(toj2i2)=Y(toj1i1)+1
(3)工件搬运时间约束,工件前道工序加工完成后才能搬运至下道工序:
S(toji)≥C(oj(i-1))+tr(μj(i-1),μji)
(4)机床加工规则约束:机床按先到先服务的规则(FCFS)加工:
C(oj2 i2)≥C(oj1 i1) +pj2 i2
∀oj1i1,oj2i2∈O,μj1i1=μj2i2,C(toj2i2)≻C(toj1i1)
(5)工件在机床上的加工过程约束:工件被搬运到机床输入缓存区等机床空闲再对其进行加工:
C(oji)≥C(toji)+pji+Wji∀oji∈O
3 调度策略
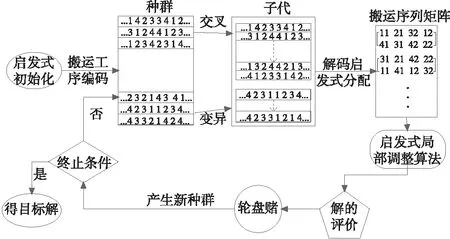
每道加工工序oij前都需要一道与之对应的搬运工序toji(第一道加工工序oj1对应从装载站M0到机床μj1的搬运工序toj1,到达卸载站Mm+1前也有一道搬运工序to(jnj+1)),且机床是按先到先服务的规则(FCFS)加工,因此只需确定每台机器人的搬运序列Seq(Rr)(即确定搬运序列矩阵Seq(R)),则可以求得到唯一的一个调度方案。
定义在时间t时机器人可行搬运工序的概念,在时间t时满足以下条件之一的待执行搬运工序称为的机器人可行搬运工序,可行搬运工序集合记为avaTR(t)=A∪B:
(1)工件第一道加工工序前的搬运工序即
A={toji|toji∈toj1,∀Jj∈J}
(2)前道加工工序已经完成的搬运工序即
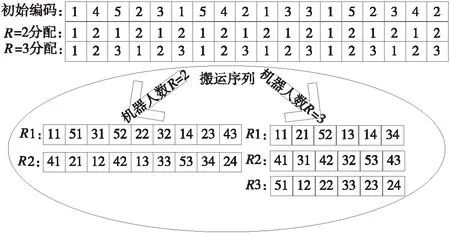
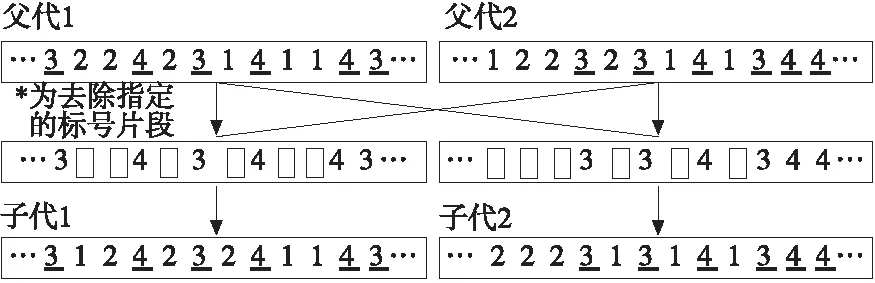
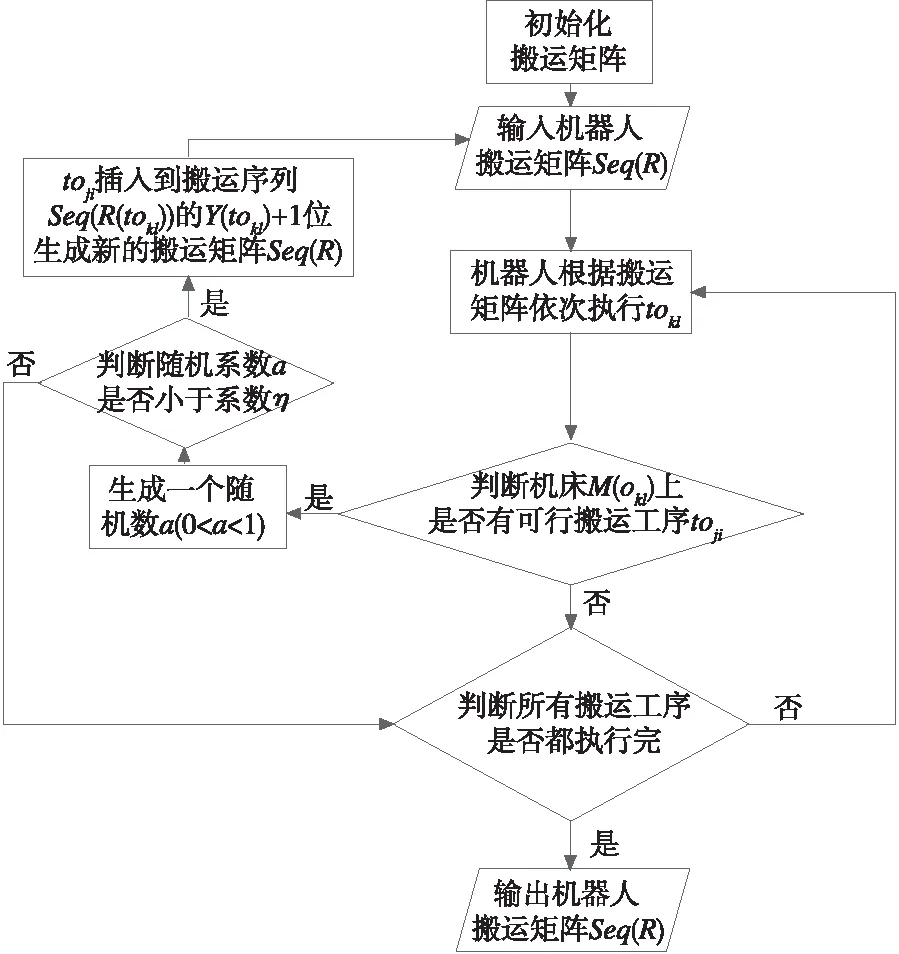
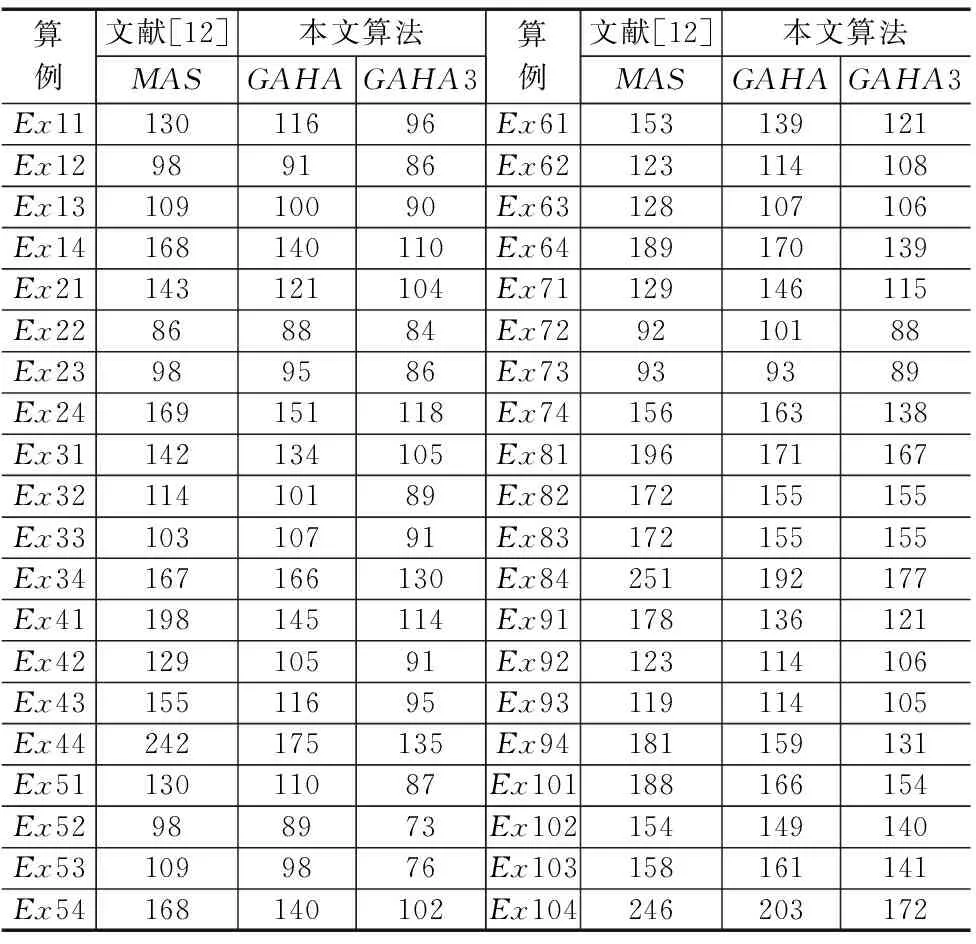
B={toji|i>1,C(oji-1) 由定义可知,机器人可行搬运工序即是时间t时在装载站或机床的输出缓存区上待机器人搬运的搬运工序。同理把时间t时在机床输入缓存区上待加工的工序称为机床在时间t可行加工工序记为: avaTM(t)={oji|C(toji) 每台机器人在时间t=0开始从其各自搬运任务序列Seq(Rr)依次选出搬运任务,判断其是否为可行搬运工序,如其为可行搬运工序则执行,否则等待,直到其变为可行搬运工序,同样,每台机床从时间t=0开始循环查询其输入缓存区上的可行加工序,并按FCFS规则依次执行,机床与机器人之间通过可行搬运工序集avaTR和可行加工工序集avaTM来保证工序约束。操作流程图如图1所示。 图1 机器人与机床执行流程图 4.1编码与解码 根据柔性机器人制造单元的特点,提出了一种仅对搬运工序编码,编码中的每个基因代表对应该数字的工件的一道搬运工序,相同数字出现次序代表该工件该道搬运工序的次序。例如图2中的基因片段1,4,5,2,3,1,5代表搬运顺序依次为to11,to41,to51,to21,to31,to12,to52,解码时根据不同的机器人数量按均匀分配的启发式规则把编码转化为机器人搬运序列矩阵。 图2 编码与搬运序列矩阵 4.2算子设计 (1)适应函数 (2)选择操作 (3)交叉操作 使用双位POX交叉方式如图3所示,它产生的子代能够很好的继承父代的优良基因。 图3 POX交叉 (4)变异操作 变异可以使算法跳出局部最优值,在更广的范围内搜索全局最优值。反序变异算子在搜索空间中搜索到的领域聚集度较高,本算法使用反序变异操作。 4.3启发式调整算法 机器人制造单元的生产过程中机器人从一台机床到另一台机床间的空载时间tr′(Mm1,Mm2)较大,它不仅影响了最大完工时间,而且增加了机器人的消耗。合理的减少空载能很大程度上减小最大完工时间。在时间t机器人Rr按搬运序列执行完成一道搬运工序tokl到达机床Mm后,如果机床Mm的输出缓存区上有可行搬运工序,则按一定的概率η(0<η<1)把搬运工序toji插入搬运序列Seq(Rr)中的Y(tokl)+1位置,启发式调整的流程如图4。 图4 启发式调整方法 4.4混合算法流程 混合遗传算法的流程如图5所示,算法结合了遗传算法的全局搜索能力和启发式调整算法的局部调整能力。 图5 混合算法流程图 引入BilgeUlusoy[11]提出的柔性制造系统调度问题的40个标准算例,对由4台机床,2台和3台机器人组成的机器人制造单元进行实验。对比组中MAS表示文献[12]中提出的算法结果。GAHA表示本文提出的混合使用改进遗传算法与启发式调整算法,GAHA3表示有3台机器人(默认情况为2台搬运机器人)。算法的参数选定为:种群规模为30、最大迭代次为1000,代沟为0.9,交叉率为0.8,变异率0.06。在MatlabR2010软件下运行,系统运行环境为Window7 64位 2.5GHz/4GRAM,对每个算例分别运行10次,取最优值。实验结果如表1所示。 通过实验结果分析可知在两台搬运机器人情况下本文提出的算法(GAHA)求得的40个标准算例结果82.5%比文献[12]求得的结果优,与文献[9]求得的结果相比,由于文献[9]中没有考虑最后一道搬至卸载站的工序,所以本算法求得的值比其大,但也比较接近。通过GAHA与GAHA3对比可知增加一台搬运机器人将加快完工时间,且搬运时间越长时增加机器人对完工时间的加快越明显。 表1 实验结果 本文提出一种对搬运工序排序组成搬运序列矩阵的调度策略,使用改进遗传算法和启发式搬运矩阵调整算法对多机器人柔性制造单元Job-shop类型调度问题进行研究,较好的解决了考虑搬运工序的多机器人制造单元Job-shop类型调度问题。以后将来将进行考虑机器柔性与工序柔性的柔性机器人制造单元多目标调度问题研究。 [1] 王凌,郑大钟. 基于遗传算法的JobShop调度研究进展[J].控制与决策,2001,16(S):642-646. [2] 熊禾根,李建军,孔建益,等.考虑工序相关性的动态Jobshop调度问题启发式算法[J].机械工程学报,2006,42(8):50-55. [3] 潘全科,王文宏,潘群,等. 解决JOBSHOP问题的粒子群优化算法[J].机械科学与技术,2006,25(6):675-679. [4] 何之洲,杨煜俊,陈新度.带搬运机器人的Job-shop问题的并行禁忌搜索算法[J].工业工程,2013,16(4):123-125. [5]ACaumond,PLacomme.AnMILPforschedulingproblemsinanFMSwithonevehicle[J].EurpeanJouralofOperationalResrarch,2009, 3(51):706- 722. [6]PhilippeL,MohandLADisjunctiveGraphforthejob-shopwithseveralrobots[c].MISTAConference. [7]HurinkJ,KnustS.Tabusearchalgorithmsforjob-shopproblemswithasingletransportrobot[J].EuropeanJournalofOperationalResearch, 2005, 162(1): 99-111. [8] 张国辉. 柔性作业车间调度方法研究[D].武汉:华中科技术大学,2009. [9]AGnanavelBabu,JJerald,ANoorulHaq.SchedulingofmachinesandautomatedguidedvehiclesinFMSusingdifferentialevolution[J].InternationalJournalofProductionResearch, 2010,48(16):4683-4699.[10] L DEROUSSI, M GOURGANDz. A simple metaheuristic approach to the simultaneous scheduling of machines and automated guided vehicles[J]. International Journal of Production Research,2008,46(8):2144- 2163. [11] U Bilge, G Ulusoy.A time window approach to simultaneous scheduling of machines and material handling system in an FMS[J].Operations Research, 1995,43(6):1058-1070. [12]Rizvan Erola, Cenk Sahina, Adil Baykasoglub,et al. A multi-agent based approach to dynamic scheduling of machines and automated guided vehicles in manufacturing systems[J].Applied Soft Computing,2012,12:1720-1732. (编辑李秀敏) Research of Flexible Robotic Manufacturing Cell Scheduling Problem Based on Hybrid Genetic Algorithm LONG Chuan-ze , YANG Yu-jun (Guangdong Provincial Key Laboratory of Computer Integrated Manufacturing System, School of Electromechanical Engineering,Guangdong University of Technology, Guangzhou 510006, China) Considering the transport time of robot among loading station machine and unloading station to solve flexible robotic manufacturing cell scheduling problem . The goal is to find the shortest time for all workpiece is completed and moved to unload station. Firstly, mathematical model is established based on analysis of the characteristics of flexible robot manufacturing cell scheduling problems. A new scheduling method based on sequence matrix of robot transport operation is proposed, machine processing is based on first come first serve rule (FCFS); Then, an improved genetic algorithm is proposed for this scheduling method ,handling procedure code method and heuristic assignment strategy for genetic algorithm is designed, heuristic handling sequence adjustment algorithm is proposed; Finally, heuristic algorithm is combined with genetic algorithm to build hybrid algorithm to solve this scheduling problem, through the standard example calculation, verified the effectiveness of the algorithm. flexible robot manufacturing cell; Job-Shop; HGA 1001-2265(2015)11-0141-04DOI:10.13462/j.cnki.mmtamt.2015.11.039 2015-01-14; 2015-02-15 国家自然科学基金资助项目(51105082);国家科技支撑计划资助项目(2012BAF12B10); 广东省战略性新兴产业核心技术攻关资助项目(2011A091101003) 龙传泽(1989—),男,江西赣州人,广东工业大学硕士研究生,研究方向为工业机器人,智能制造, (E-mail)oklongmm@qq.com。 TH166;TG506 A
4 算法设计
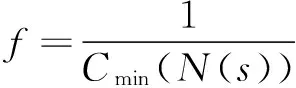
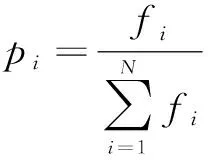
5 算例分析
6 结束语
